周报：2021-1-18~2021-1-24

---

本周工作：

• Xiong Z , Wang L , Li H , et al. Snapshot Hyperspectral Light Field Imaging[C]// 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE, 2017.

• Single-shot three-dimensional imaging with a scattering layer

• Rueda H , Arguello H , Arce G R . High-dimensional optimization of color coded apertures for compressive spectral cameras[C]// 2017 25th European Signal Processing Conference (EUSIPCO). 2017.

Paper 1

Title

《散射层快照高光谱成像》

Single-shot three-dimensional imaging with a scattering layer

Contents

本文提出了一种基于 Scattering layer 的快照式高光谱相机，通过将一片薄散射层（scattering layer）放置于一个2D成像传感器前，形成一个 类光场相机。利用散射层散射出的光斑具有 数据独立性和空间遍历性 的特征，来实现三维重建（注：此处的第三维 是指 深度 维度）。

Theory

散射层具备自己独特的Point spread function (PSF)，理论表示如下：

将统计学理论应用，$s_j$和$S(r)$的协方差可以表示为：

$$C_j(\hat r) = \int {s_j(r+\hat r)S(r)dr}$$

散射层散射出的光斑图样具有统计学特征，充分发展的光斑图样具有沿中心呈负指数分布的特点，其方差等于均值的平方，基于moment factoring theorem 和 Van Cittert - Zernike theorem，上面的式子可以简化为：

$$C_j (\hat r) = |\Gamma_j(\hat r)|^2 + \bar S\bar {s_j}$$

其中$\Gamma_j(r)$ 代表block函数的功率谱。

根据傅里叶切片定理，可以证明：

$$|\Gamma(0)|^2 = \bar S\bar {s_j}, |\Gamma(r)|^2\approx 0\ when\ r>>0$$

Calibration

本文将scattering layer 放置在一个多孔孔径后面，通过开关孔径窗口实现指定位置的scattering layer的打开与关闭。

在标定过程种，本文应用了沿着深度方向上的按比例放大缩小的近似原理：

因此，只需要在一个参考深度下标定一个2D平面的点即可。

Experiment

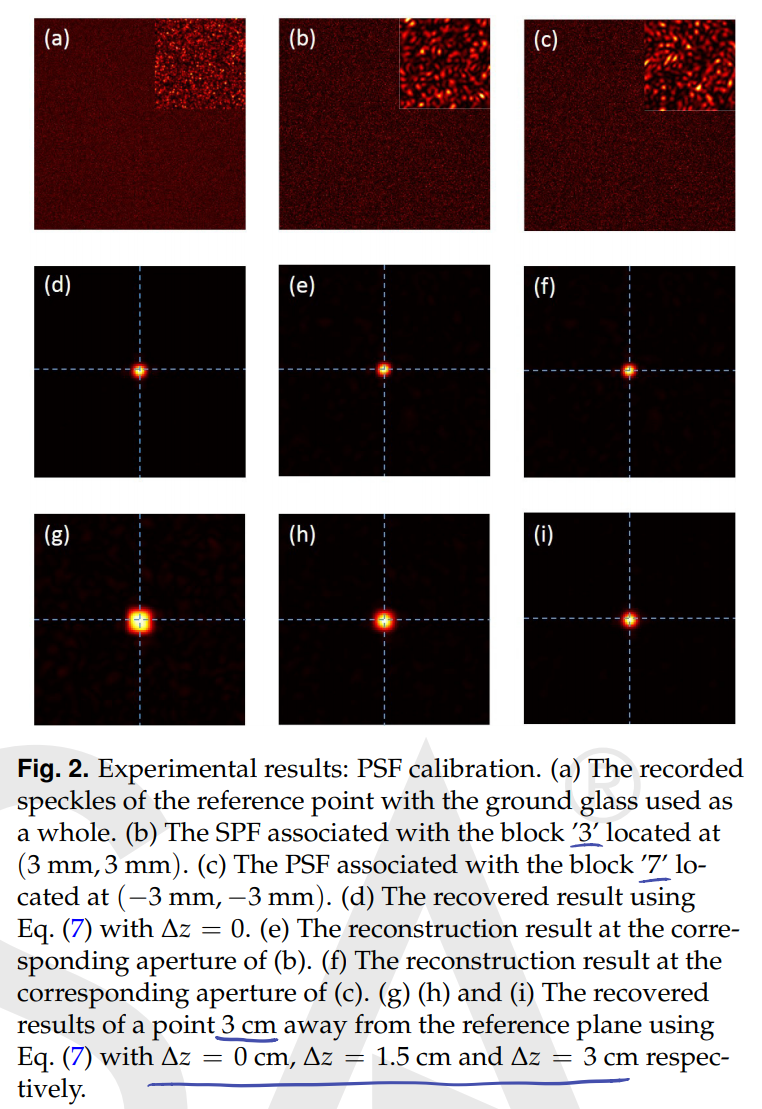
本文以9个正方形孔为例，首先轮流打开每一个小孔并标定PSF，最后通过全开所有孔测出所测物体在scattering layer成像所形成的光斑图像，然后应用理论，将该图像与每一个孔的PSF求协方差，得到每个孔角度下的该物体的成像。

标定实验图：

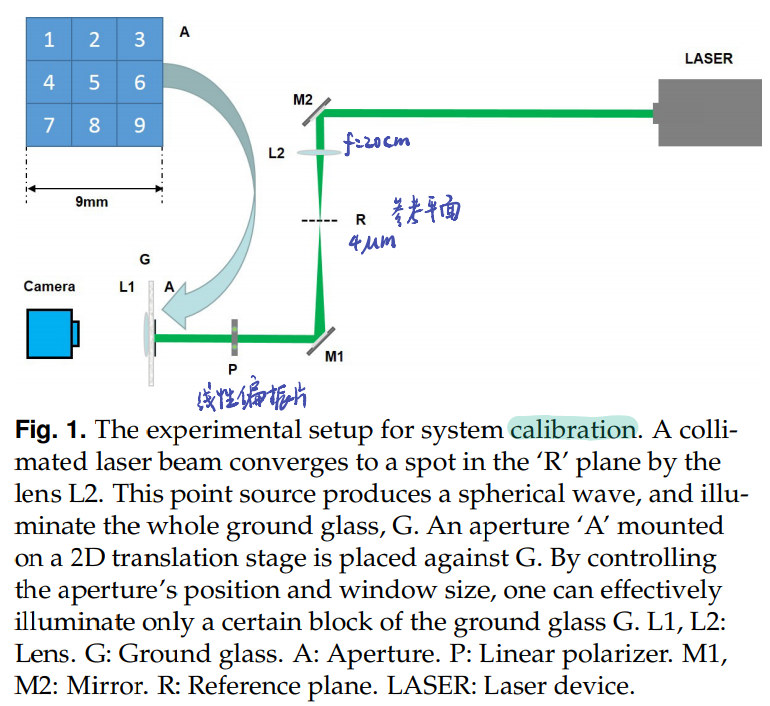
成像实验中，在不同深度（深度差为5cm）放置了两个物体：X 和 3

成像实验图：

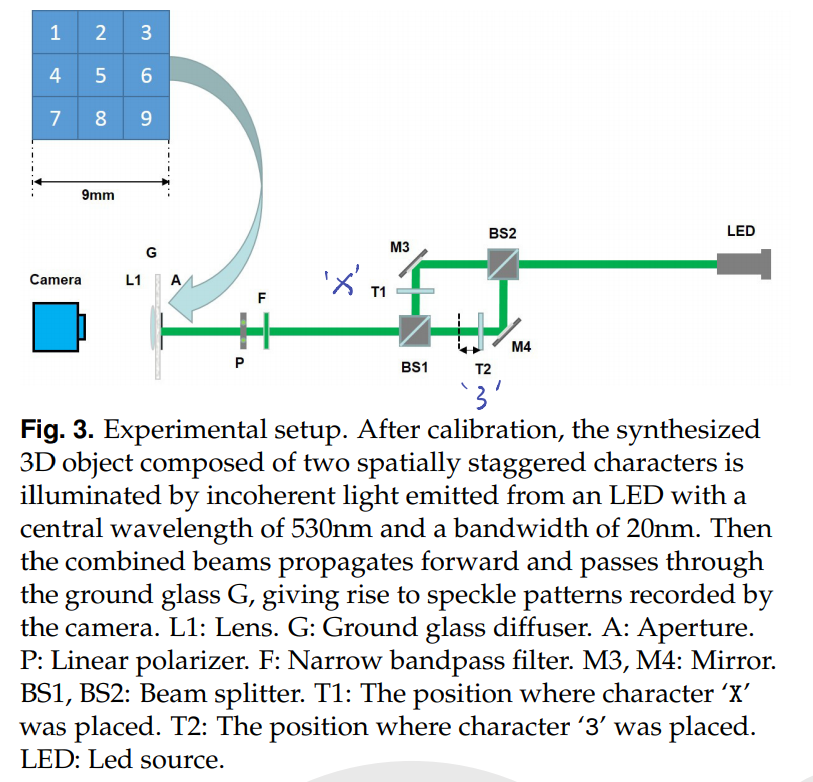
Results

可以看出，在开不同窗口时，位于焦平面上的X并没有受到影响，但是不在焦点处的3的光强具有显著变化，当全开窗口时，可以明显看出来深度上的差异，同时，图(f)将PSF中的$\Delta z$调为了50cm，因此此刻呈现的图像等价于3处在焦平面上。

Paper 2

Title

《高维彩色编码孔径最优化下的压缩光谱成像》

Rueda H , Arguello H , Arce G R . High-dimensional optimization of color coded apertures for compressive spectral cameras[C]// 2017 25th European Signal Processing Conference (EUSIPCO). 2017.

Contents

本文提出了一种编码孔径最优化设计方案，并利用迭代算法实现，相对于传统的随机生成编码孔径有8dB的提高。

Theory

作者将RIP条件中的矩阵$\mathbf {A_{|\rho||\rho|}}$：

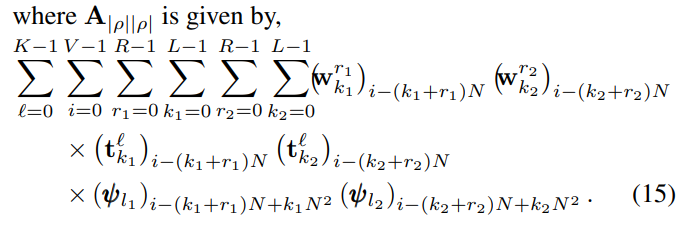
中的关于编码孔径的一项单独拎出来作为一个系数$\beta$：

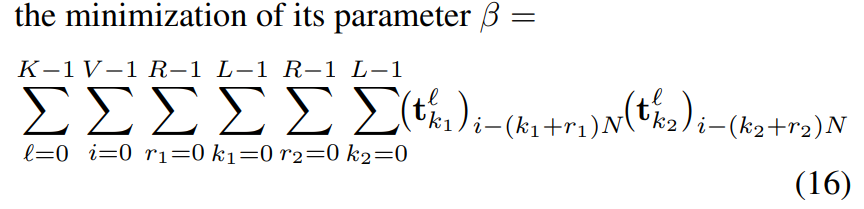
RIP条件证明我们需要使系数$\beta$越小越好，因此需要寻找上式最小值时的矩阵$\mathbf t$，将编码孔径矩阵拆分为三维结构形式$(R+L)\times (R+L)\times L$，并将优化问题写成如下形式：

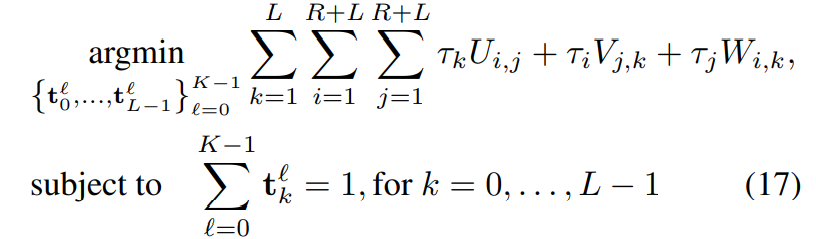
其中 $U{i,j},V{i,j},W{i,j}$分别代表 $x-y,y-\lambda,x-\lambda$的控制项，$\tau{i/j/k}$为权重系数。

作者提出了新的迭代算法实现这样的优化问题求解：

Results