周报：2020-12-21~2020-12-27

本周主要做了以下工作：

阅读两篇 UC Berkeley 计算成像实验室的论文：

  1. Antipa N , Kuo G , Heckel R , et al. DiffuserCam:lensless single-exposure 3D imaging[J]. Optica, 2018.

学习 上面两篇论文的 Diffuser Cam源码 DiffuserCam

Paper 1

Title

《漫射相机：无镜片单曝光三维成像》

Antipa N , Kuo G , Heckel R , et al. DiffuserCam:lensless single-exposure 3D imaging[J]. Optica, 2018.

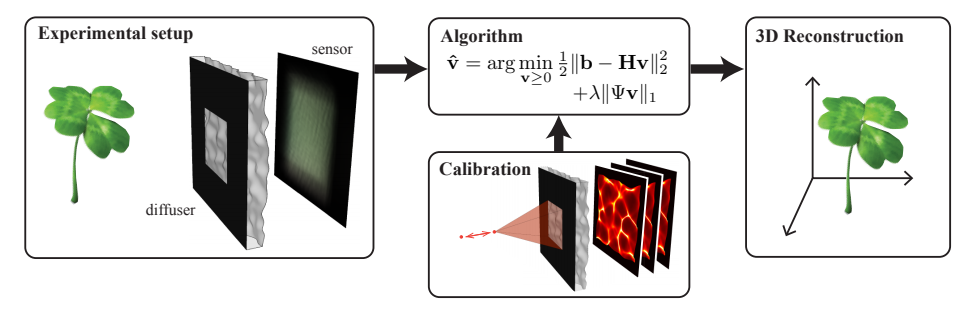
Contents

作者提出了一种基于diffuser（漫射片，毛玻璃片）的无物镜三维成像系统，由于每一个空间位置的点光源都能够通过diffuser产生伪随机折射最终在sensor上呈现出一种 caustics（焦散线）的图案，在数学上 称为Point Spead Functions (PSFs)，便能够通过一些标定手段获得diffuser对于三维空间中每一个空间点对应到sensor上一个图案的传递函数（矩阵），结合压缩感知和最优化算法，进而实现通过混杂的二维sensor图案反演得到三维原图像。

本文针对大规模的（100million）像素块标定过程，引入了shift invariance assumption（位移不变性假设）和paraxial approximation（近轴近似），将标定规模降低至仅需标定 0轴 的范围，大大降低标定复杂度。

实验器材仅需：diffuser、sensor、aperture（用来控制diffuser成像投影在sensor上的大小）

大致的实验模型如下：在diffuser前加一个aperture，后方放置sensor 即可

image-20201227162038327

通过 z轴 标定后得到H矩阵，应用最优化算法即可得到三维成像结果。

Specifics

设 sensor上图案矩阵的向量表示为 $\mathbf b$，diffuser的传递矩阵为 $\mathbf H$，三维场景元素矩阵的向量表示为 $\mathbf v$，则 有：

式中，$\mathbf H$ 的每一列都代表 三维场景中单个像素块对sensor的所有元素的贡献。

需要求解的问题，即：

为了应用压缩感知，需要 $\mathbf H$ 满足

  1. 每列都尽量不相关
  2. 焦散图案需要较高的空间频率

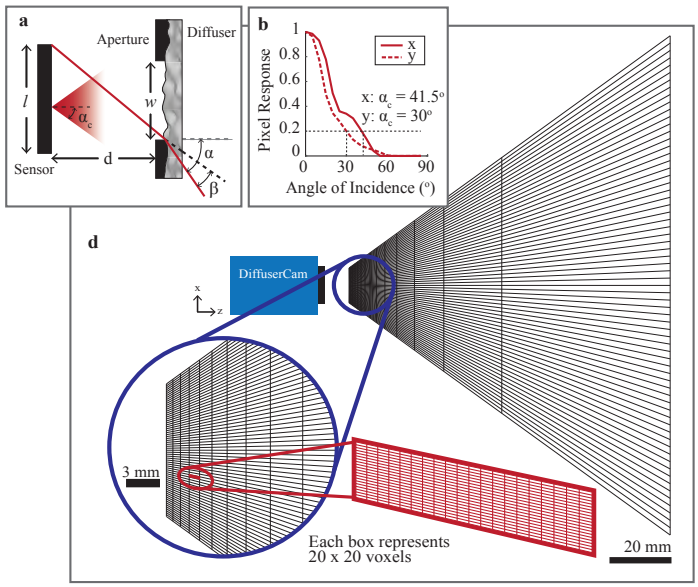
本实验装置有两个特性参数需要控制：

  1. 焦比 f-number（焦距与光圈比值）：决定了成像分辨率
  2. 平均焦距：决定了最佳放置sensor的位置

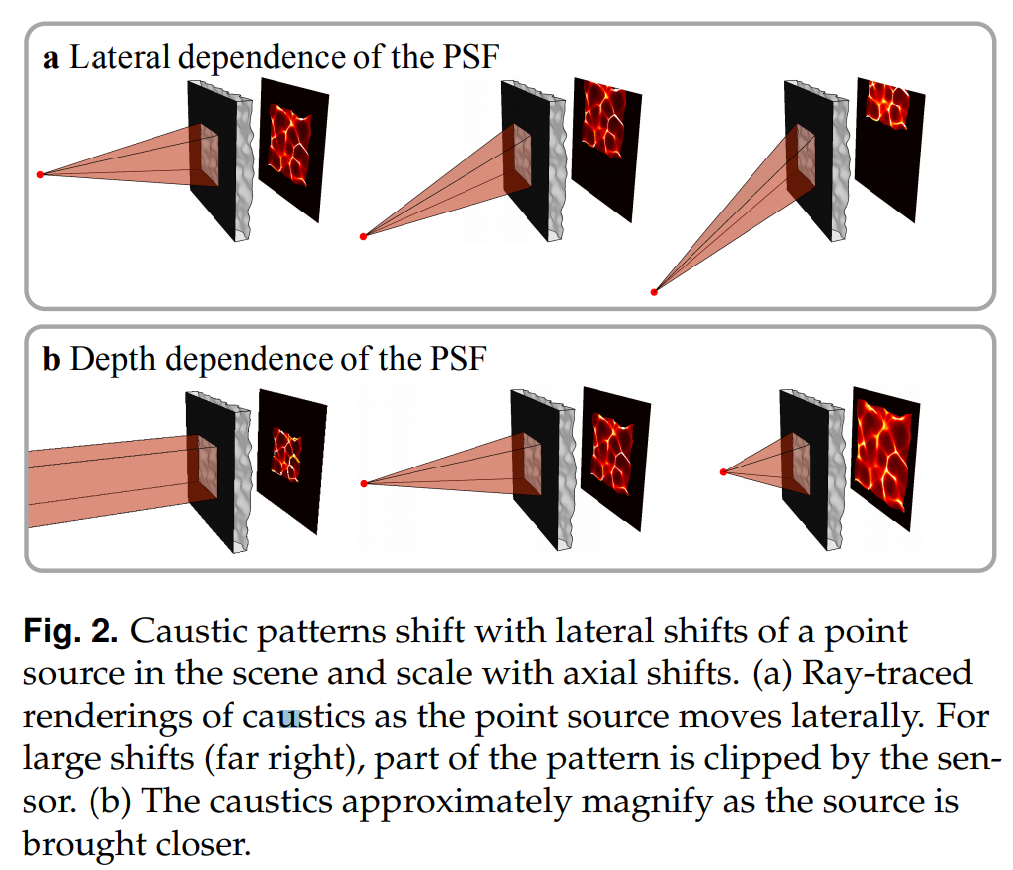
此外，还需要考虑的问题是 轴向位置的影响、侧向位移的影响

image-20201227165956486

此处，在计算矩阵乘法 $\mathbf {Hv}$ 时，写成求和式，如下：

计算复杂度过高，从而引入了shift invariance assumption（位移不变性假设）和paraxial approximation（近轴近似），将同一 z轴坐标的 不同 $(x,y)$ 像素值产生的对sensor的成像近似为 正比于 同一z轴坐标 在$(0,0)$处产生的对sensor的成像，这样一来，上式的计算可以消掉两个维度：

$h(x’,y’;x,y,z) = h(x’+mx,y’+my;z)$

从而有：

image-20201227170944901

其中，$*$ 表示求三维离散卷积，这种模型为本文提出的 convolution model，它拥有一些优点：

  1. 使得计算每 $\mathbf {Hv}$ 变得更简单
  2. 它提供了一个本系统满足稀疏性的一个有效的证据
  3. 使得标定过程变得更简单

在求解这样一个最优化模型时，由于规模太大，梯度投影计算复杂度过高，因此作者应用了针对大规模的ADMM算法（交替方向乘子法）(详情见2011年论文 S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein, “Distributed optimization and statistical learning via the alternating direction method of multipliers,” Foundations and Trends in Machine Learning 3, 1–122 (2011).)，因此需要变量分离操作（查了一下，ADMM是双变量迭代优化算法）：

image-20201227171441778

image-20201227172301162

经过分析，总的计算复杂度为 $O(n^3logn)$，受制于三维FFT复杂度。

此外，本文还提到了成像角度问题，最终设置了x和y方向的两个满足 两点分辨率的临界角度 $41.5°，30°$

image-20201227172640721

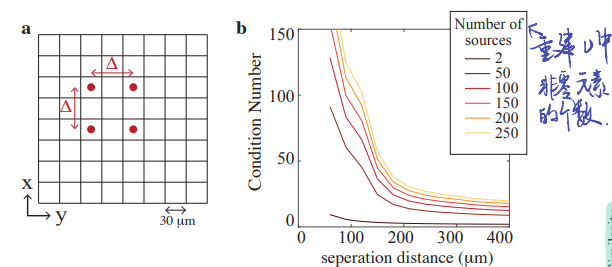
同时，作者提出了一种新的分辨率判别形式用来：multi-point resolution，即多点分辨率，此处是16个点。因为作者发现 本实验装置的重建分辨率与成像物体的复杂性有关，复杂的物体重建，多点分辨率设定会比两点的更优。

针对分辨率问题，作者提出了 Local condition nuber theory（局部条件数理论），即 定义局部条件数为成像的 $\mathbf v$ 中非零元素的数量，显然，非零元素越多，效果越差（混杂现象多）。

image-20201227174100537

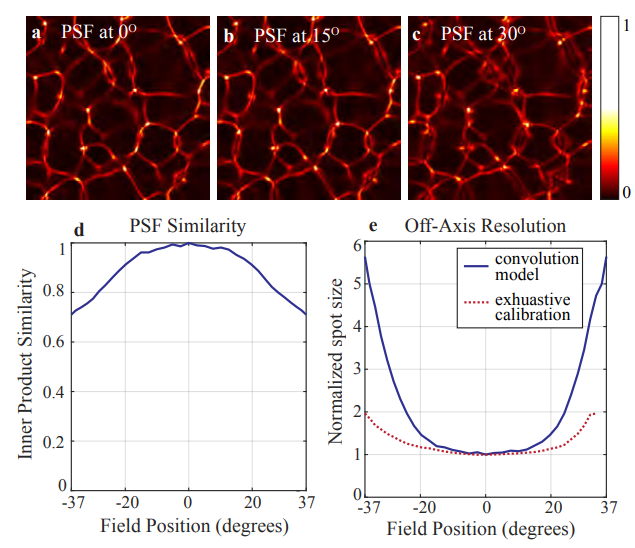
在实验阶段，作者为了验证近轴近似的正确性，在同一z轴坐标下，测出了不同角度的PSF图像，并将所有角度的PSF与0°的PSF作内积，并对比，得到图像：

image-20201227174421944

理论上来讲，同意z轴坐标下所有角度的PSF都是相同的，从上图的结果来看，所有角度的PSF最差也有75%的相似度，因此可以认为近似成立。

上图右下角的子图中，蓝色实线为所有重建的单点峰宽与重建0°点的峰宽比值，并用0°点峰宽做标准化，红色点线为实行完全标定的结果（误差很小），然而为了降低复杂度，本实验仍然使用简化的标定方法。

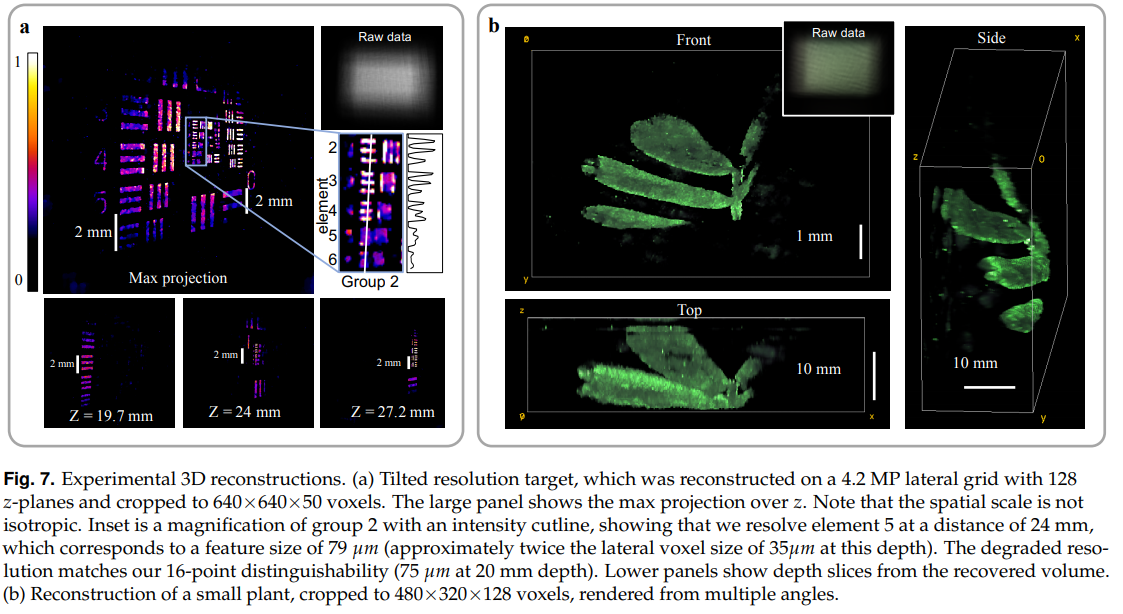
Experiments & Results

实验采用128个z轴平面，z=10.86mm ~ 36.26mm，三维图像在 $2048\times 2048\times 128$ 网格上重建，重建物体为USAF1951分辨率板和一株绿色植物，结果如下：

image-20201227175627628

图像处理知识点

关于cv2和matplotlib的imshow区别

  • opencv存储图像默认 BGR 顺序，PIL的Image读取默认RGB

  • opencv的imshow默认opencv格式，matplotlib的imshow默认RGB格式

建议尽量不要混用，如果非要的话，可以用以下方式处理：

1
2
3
4
# cv2读入，plt.imshow显示图像
img = cv2.imread('lena.jpg')
img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB) # 需要转换成RGB
plt.imshow(img)

关于fft计算线性卷积 和 (i)fftshift的作用

在数学与信号处理种，通常计算信号的卷积 是 将其通过傅里叶变换转换到频域，然后计算频域的乘积，再逆变换回去，DFT的快速算法是FFT，时间复杂度$O(nlogn)$，其具体实现见 我的blog：FFT及其优化，然而，可以证明FFT计算得到的其实是循环卷积，并不是我们通常想得到的线性卷积。

为了解决上述问题，需要再傅里叶变换前进行一些操作，称之为padding 0（在卷积神经网络中又学到过，即 补零操作），之后再进行FFT就能得到线性卷积（可以严格证明）。

为了将频谱零频点移动到图像中央，我们需要对原图进行 (i)fftshift 操作

  • fftshift 将信号（图像）向正方向（右下）移动一半尺寸的位置

  • ifftshift 将信号（图像）向负方向（左上）移动一半尺寸的位置

上述的 一半尺寸 指：偶数$\frac n 2$，奇数$\frac{n-1}2$

因此，在求卷积之前，我们都需要进行 (i)fftshift 操作

FISTA Algorithm

FISTA（快速迭代阈值收缩算法）基于梯度下降，收敛复杂度为$O(1/k^2)$，比传统的ISTA（复杂度 $O(1/k)$）更快。

参考UC Berkeley计算成像实验室代码：

code 
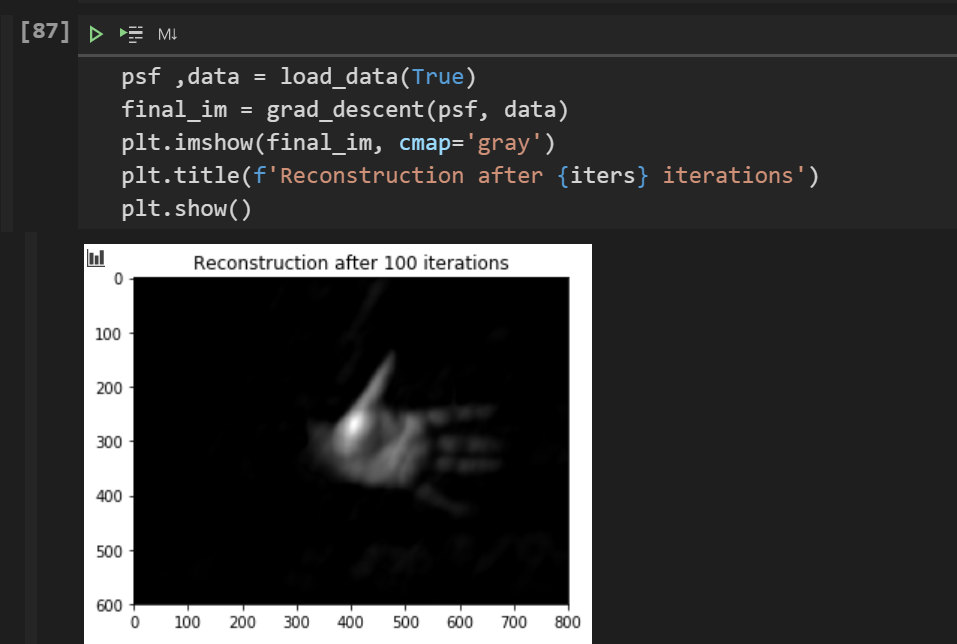
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
# To add a new cell, type '# %%'
# To add a new markdown cell, type '# %% [markdown]'

# %%
from PIL import Image
import matplotlib.pyplot as plt
import numpy as np
import numpy.fft as fft
from IPython import display
import cv2


# %%
f = 1/8
psf_data = 'psf_sample.tif'
raw_data = 'rawdata_hand_sample.tif'
iters = 100
def load_data(show_im=True):
    psf = Image.open(psf_data)
    data = Image.open(raw_data)
    psf = np.array(psf,dtype='float32')
    data = np.array(data,dtype='float32')
    print(f"origin_size_psf: {psf.shape}")
    print(f"origin_size_rawdata: {data.shape}")

    # reduce noise
    noise = np.mean(psf[5:15,5:15])
    psf -= noise
    data -= noise

    def resize(img,factor):
        num = int(-np.log2(factor))
        for i in range(num): # use 2x2 box to do convolution
            img = 0.25 * (img[::2,::2,...]+img[1::2,::2,...]+img[::2,1::2,...]+img[1::2,1::2,...])
        return img

    psf = resize(psf, f)
    data = resize(data, f)

    psf /= np.linalg.norm(psf.ravel())
    data /= np.linalg.norm(data.ravel())
    print(f"new_size_psf: {psf.shape}")
    print(f"new_size_data: {data.shape}")
    if show_im:
        plt.figure(figsize=(12,8))
        plt.subplot(1,2,1)
        plt.imshow(psf, cmap='gray')
        plt.title('psf')
        plt.subplot(1,2,2)
        plt.imshow(data, cmap='gray')
        plt.title('raw_data')
        plt.show()
    return psf,data
hahaha = load_data()


# # %%
# def shift():
#     delta = np.zeros((5,5))
#     delta[2][2] = 1
#     delta_shifted = fft.ifftshift(delta)
#     fft_mag = np.abs(fft.fft2(delta_shifted))
#     fft_arg = np.angle(fft.fft2(delta_shifted))
#     fft_mag_o = np.abs(fft.fft2(delta))
#     fft_arg_o = np.angle(fft.fft2(delta))

#     plt.figure(figsize=(8,6))

#     plt.subplot(2,3,1)
#     plt.imshow(delta,cmap='gray')
#     plt.title('origin delta')
#     plt.subplot(2,3,2)
#     plt.imshow(fft_mag_o,vmin=-3,vmax=3,cmap='gray')
#     plt.title('magnitude origin delta')
#     plt.subplot(2,3,3)
#     plt.imshow(fft_arg_o,vmin=-3,vmax=3,cmap='gray')
#     plt.title('phase origin delta')
    
#     plt.subplot(2,3,4)
#     plt.imshow(delta_shifted,cmap='gray')
#     plt.title('shifted delta')
#     plt.subplot(2,3,5)
#     plt.imshow(fft_mag,vmin=-3,vmax=3,cmap='gray')
#     plt.title('magnitude shifted delta')
#     plt.subplot(2,3,6)
#     plt.imshow(fft_arg,vmin=-3,vmax=3,cmap='gray')
#     plt.title('phase shifted delta')
#     plt.show()

# shift()


# %%
def nxt2(x):
        return int(2**np.ceil(np.log2(x)))
def init_mat(h):
    pixel_start = (np.max(h) + np.min(h)) / 2
    x = np.ones(h.shape) * pixel_start

    padded_shape = [nxt2(2*n-1) for n in h.shape]
    starti = (padded_shape[0] - h.shape[0]) // 2
    endi = starti + h.shape[0]
    startj = (padded_shape[1] - h.shape[1]) // 2
    endj = startj + h.shape[1]
    hpad = np.zeros(padded_shape)
    hpad[starti:endi,startj:endj] = h

    H = fft.fft2(fft.ifftshift(hpad), norm='ortho')
    HH = np.conj(H)
    
    def crop(X):
        return X[starti:endi,startj:endj]
    
    def pad(v):
        vpad = np.zeros(padded_shape).astype(np.complex64)
        vpad[starti:endi,startj:endj] = v
        return vpad
    
    utils = [crop, pad]
    v = np.real(pad(x))

    return H,HH,v,utils


# %%
def grad(AH, H, vk, b, crop, pad):
    Av = calcA(H, vk, crop)
    diff = Av - b
    return np.real(calcAHerm(AH, diff, pad))

def calcA(A, vk, crop):
    Vk = fft.fft2(fft.ifftshift(vk))
    return crop(fft.fftshift(fft.ifft2(A * Vk)))

def calcAHerm(AH, diff, pad):
    xpad = pad(diff)
    X = fft.fft2(fft.ifftshift(xpad))
    return fft.fftshift(fft.ifft2(AH * X))


# %%
def grad_descent(h, b):
    H, HH, v, utils = init_mat(h)
    crop, pad = utils[0],utils[1]

    alpha = np.real(1.8/(np.max(HH * H)))
    iterations = 0

    def non_neg(xi):
        xi = np.maximum(xi, 0)
        return xi

    proj = non_neg

    parent_var = [H, HH, b, crop, pad, alpha, proj]

    vk = v

    tk = 1
    xk = v

    for iterations in range(iters):
        vk, tk, xk = fista_update(vk,tk,xk,parent_var)
        if iterations % 10 == 0:
            image = proj(crop(vk))
            plt.imshow(image, cmap='gray')
            plt.title(f'Reconstruction after iteration {iterations}')
            plt.show()
            display.clear_output(wait=True)
    
    return proj(crop(vk))


# %%
# normal gradient descent
def gd_update(vk, parent_var):
    H, HH, b, crop, pad, alpha, proj = parent_var
    gradient = grad(HH, H, vk, crop, pad)
    vk -= alpha * gradient
    vk = proj(vk)
    return vk


# %%
# momentum
def nesterow_udpate(vk, p, mu, parent_var):
    H, HH, b, crop, pad, alpha, proj = parent_var
    
    p_prev = p
    gradient = grad(HH, H, vk, b, crop, pad)
    p = mu * p - alpha * gradient
    vk += -mu * p_prev + (1 + mu) * p
    vk = proj(vk)
    
    return vk, p


# %%
# FISTA algorithm
def fista_update(vk, tk, xk, parent_var):
    H, HH, b, crop, pad, alpha, proj = parent_var

    xk1 = xk
    gradient = grad(HH, H, vk, b, crop, pad)
    vk -= alpha * gradient
    xk = proj(vk)
    tk1 = (1 + np.sqrt(1 + 4 * tk * tk)) / 2
    vk = xk + (tk - 1) / tk1 *(xk - xk1)
    tk = tk1
    return vk, tk, xk


# %%
psf ,data = load_data()
final_im = grad_descent(psf, data)
plt.imshow(final_im, cmap='gray')
plt.title(f'Reconstruction after {iters} iterations')
plt.show()


# %%

成像结果：

image-20201227180224551

项目记录
周报

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！