周报：2020-12-14~2020-12-20

本周主要研读了以下内容：

  • 中科院大学的刘铭鑫博士 的博士学位论文《基于压缩感知的编码孔径光谱成像技术研究》
  • Correa C V , Arguello H , Arce G R . Spatio-spectral uniform multi-frame coded apertures for compressive spectral imaging[C]// IEEE Global Conference on Signal & Information Processing. IEEE, 2015.
  • Rueda H , Lau D , Arce G R . RGB detectors on compressive snapshot multi-spectral imagers[C]// IEEE Global Conference on Signal & Information Processing. IEEE, 2015.
  • Rueda H , Arguello H , Arce G R . Colored coded aperture compressive spectral imaging: Design and experimentation[C]// 2015 IEEE Global Conference on Signal and Information Processing (GlobalSIP). IEEE, 2015.
  • Rueda H , Arguello H , Arce G R . DMD-based implementation of patterned optical filter arrays for compressive spectral imaging[J]. Journal of the Optical Society of America A Optics Image Science & Vision, 2015, 32(1):80-9.

Paper 1

Title

《空间-光谱均匀多帧/多框架编码孔径压缩光谱成像》

Correa C V , Arguello H , Arce G R . Spatio-spectral uniform multi-frame coded apertures for compressive spectral imaging[C]// IEEE Global Conference on Signal & Information Processing. IEEE, 2015.

Contents

取代随机分布的编码孔径，作者提出了一种新型的编码孔径（空间-光谱均匀编码孔径，简称SUM）

模型还是CASSI经典模型，公式如下：我在下方补充说明了一下，g为投射在探测器上的光强，F是初始光源，T为编码孔径矩阵，ω是噪声。关于式子中是$(m+k)$还是$(m-k)$并不重要，这取决于怎样定义色散轴的正方向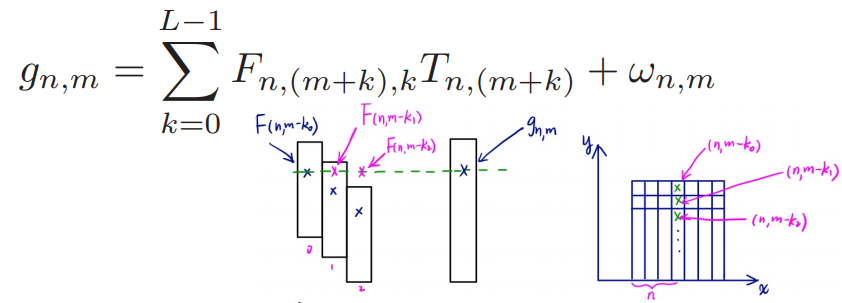image-20201217215735098

使用单个编码孔径，最后投射到探测器上的有$N(N+L-1)\times N = NV$个元素，而初始有$N\times N\times L$个元素，因此压缩率为$NV/N^2L \approx 1/L$

如果使用$K$个编码孔径，则投射到探测器上有$KNV$个元素，因此采样率为$KNV/N^2L \approx K/L$

将$K$个编码孔径矩阵拼在一起，写成列向量的形式：

下图呈现了一个$K=2,N=4,L=3$的编码孔径矩阵的结果

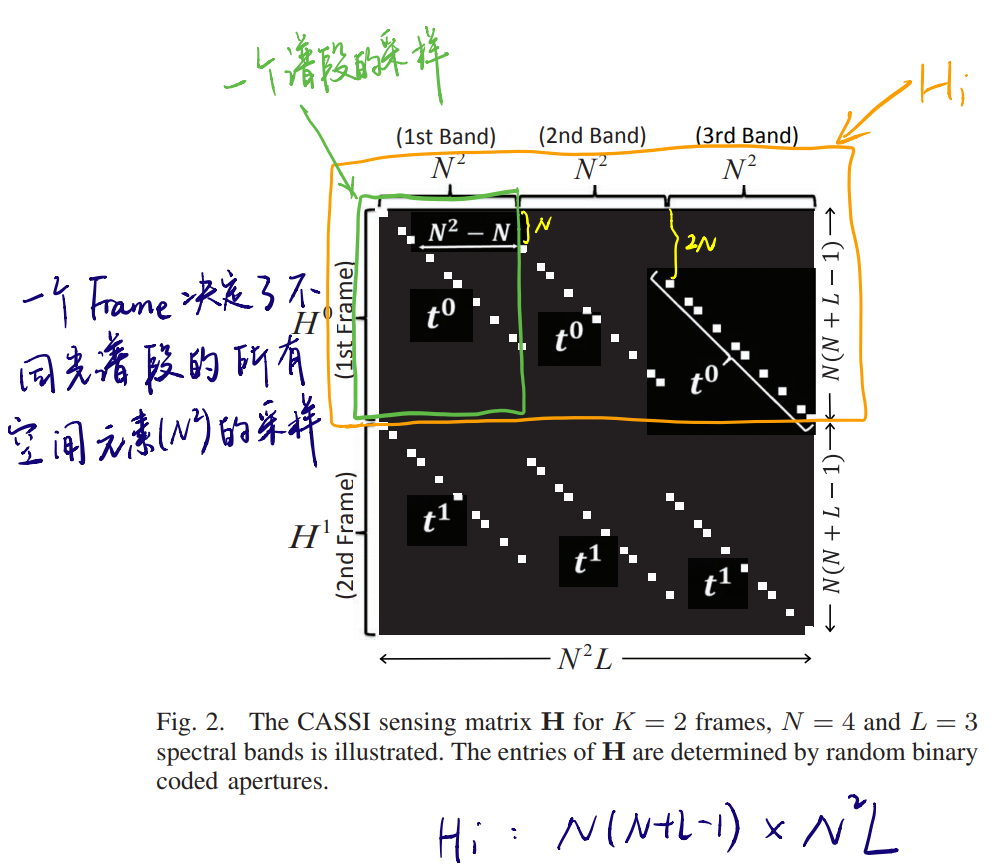
image-20201217220837061

我做了一些注释，很好理解：

  • 横向子矩阵是同一个编码孔径对不同波段的采样结果，相邻的两个矩阵右边的会比左边的低$N$个元素的位置，这是因为每产生一次色散，该波段的图像就会偏离$N$个元素的位置，所以每个子矩阵的大小都是$N(N+L-1)\times N^2$

  • 纵向则代表不同的编码孔径对应的矩阵$\mathbf H_i$

根据RIP条件（约束等距性条件），作者提出了一种生成SUM编码的算法

image-20201217222019368

Experiments & Results

1

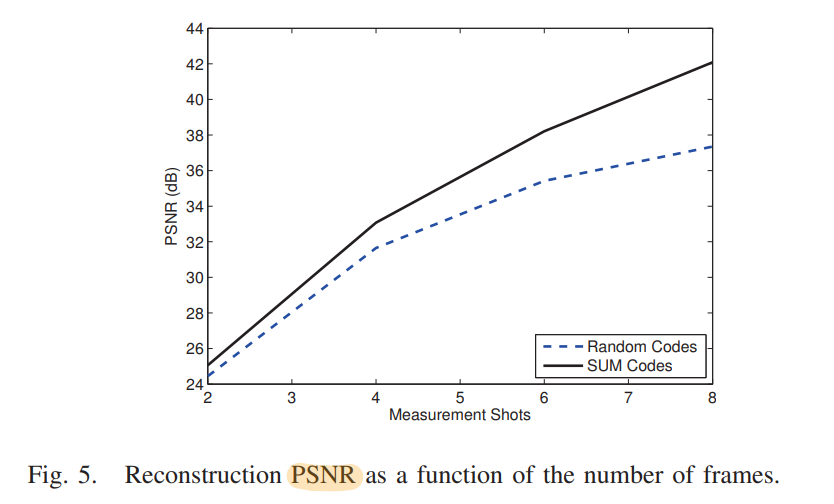
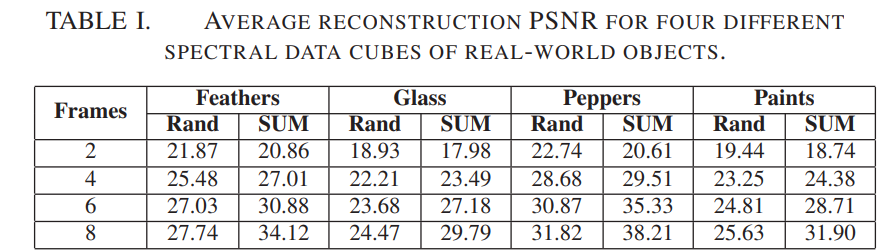
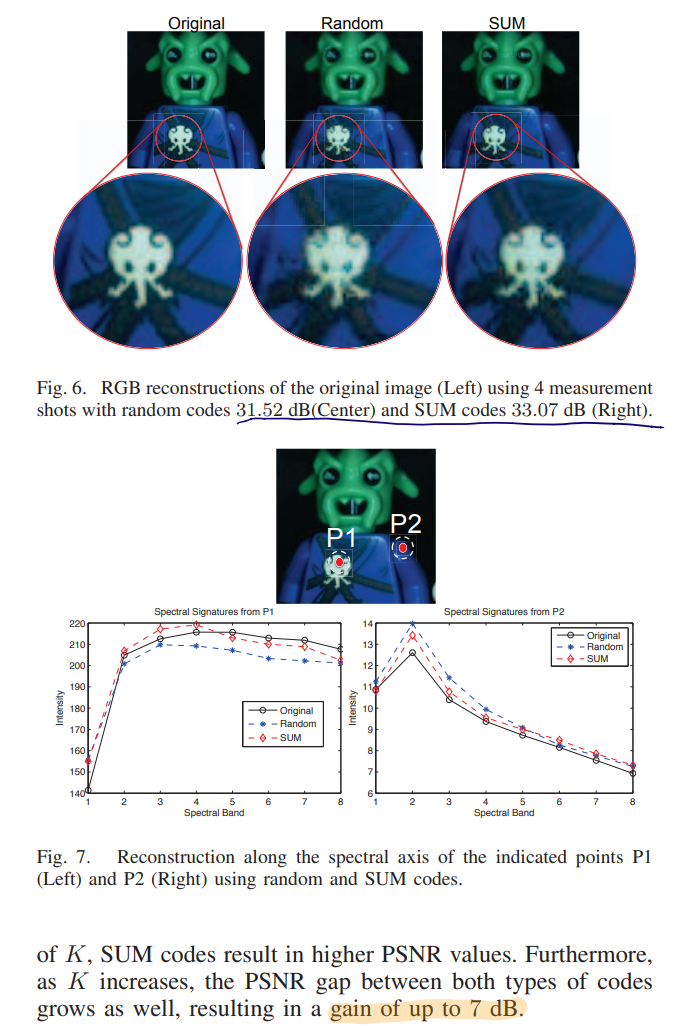
使用空间分辨率为$128\times 128$，8个光谱段，光谱带介于450nm~620nm之间，做对比实验：伯努利随机分布的编码孔径($p=0.5$) 和 SUM编码孔径

image-20201217222219726

发现SUM结果好于random：

image-20201217222252229

2

使用$128\times 128$像素，30个光谱段，400nm~700nm，K（编码孔径种类数）取2,4,6,8

image-20201217222416336

image-20201217222432892

Paper 2

Title

《基于RGB探测器的压缩快照多光谱成像仪》

Rueda H , Lau D , Arce G R . RGB detectors on compressive snapshot multi-spectral imagers[C]// IEEE Global Conference on Signal & Information Processing. IEEE, 2015.

Contents

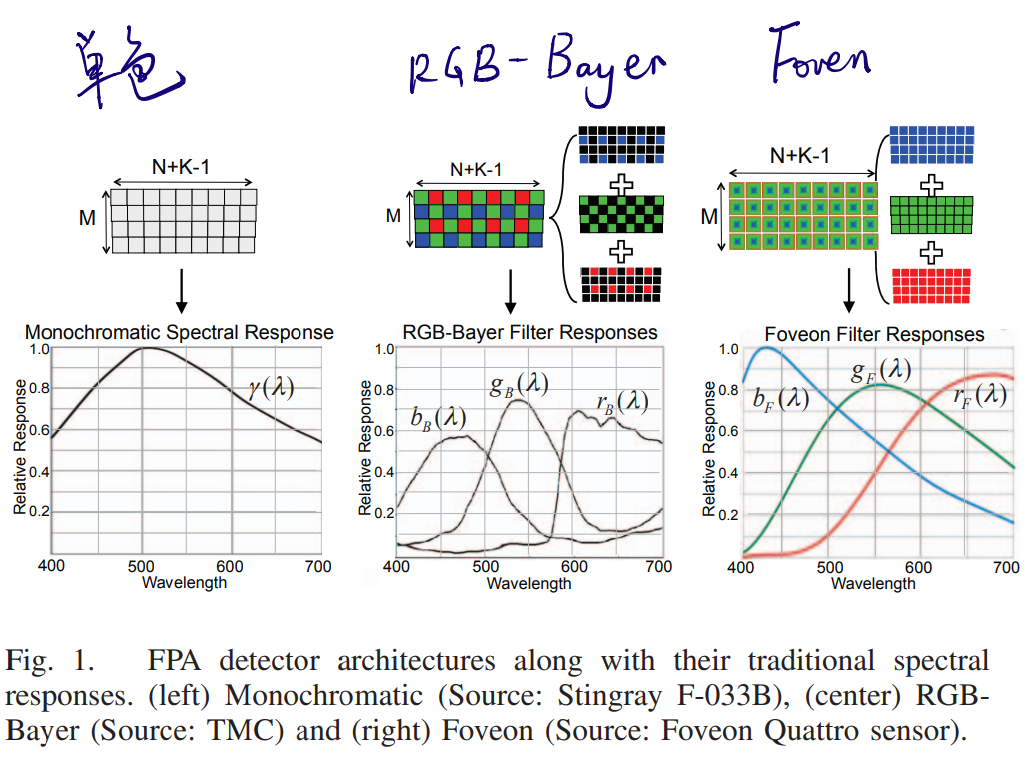
本文主要使用并对比了三种FPA探测器：

  1. 传统单色（monochromatic）探测器
  2. RGB-Bayer探测器（拜尔探测器）
  3. Foven探测器

image-20201219192736580

在数学模型中，作者将其写成了如下格式：

其中，$\mathbf T$代表编码矩阵，$\mathbf P$代表色散矩阵，$\mathbf X$代表FPA响应矩阵

仍旧需要解决一个带L1正则化的欠定最小二乘问题：

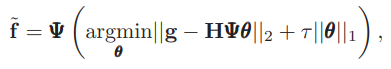
image-20201219193059421

Experiments

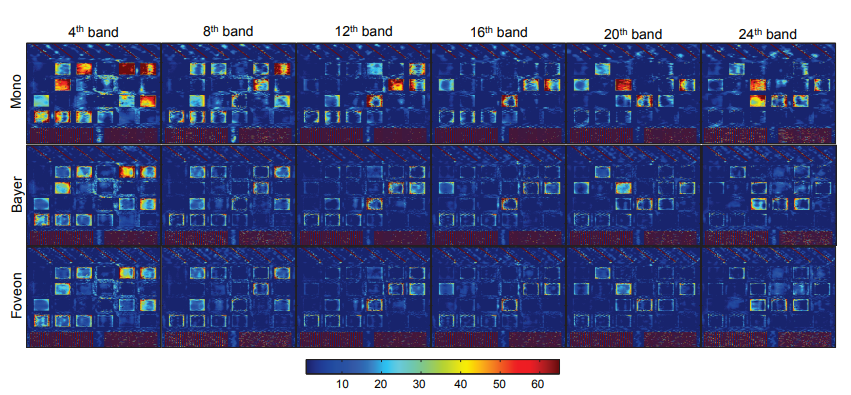
实验采用 宽带氙气灯 作为光源，光谱带宽范围为 450nm~670nm，光源像素为$256\times 256$，光谱数量$L=24$，编码孔径编码方式采用$p=0.5$的伯努利随机分布，优化算法采用GPSR，定义压缩率$R=K/L$，其中K为快照拍摄次数（注意：每一次拍照都换一个新的编码孔径）。

结果如下：

image-20201219193435370

绝对误差图如下：

image-20201219194136329

之后，作者又测试了两组数据立方体，L=31，分辨率$512\times 512$，结果分别如下：

image-20201219194244203

image-20201219194256647

Results

结果显示，相较于传统的单色传感器：

  • Foveon 传感器 有 3dB 的提升
  • Bayer 传感器 有 2dB 的提升

Paper 3

Title

《颜色编码孔径压缩光谱成像：设计与实验》

Rueda H , Arguello H , Arce G R . Colored coded aperture compressive spectral imaging: Design and experimentation[C]// 2015 IEEE Global Conference on Signal and Information Processing (GlobalSIP). IEEE, 2015.

Contents

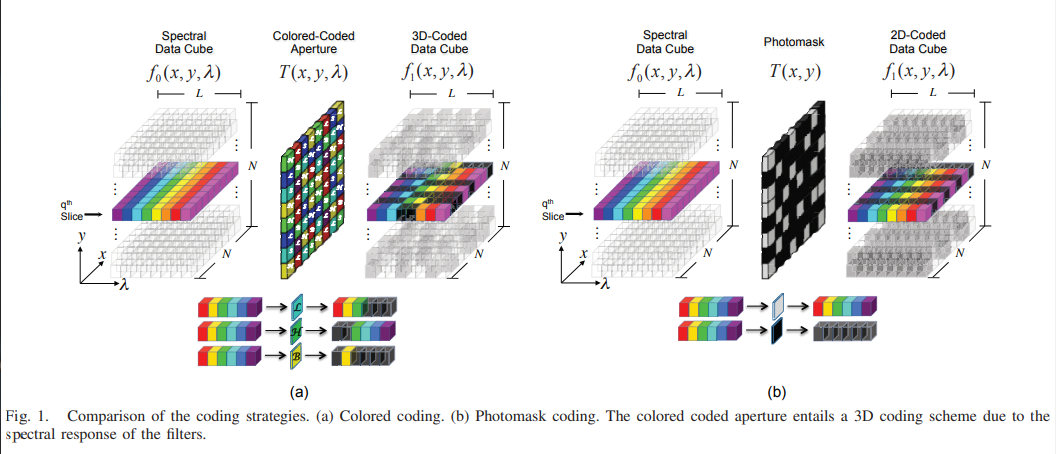
本文的方法类似于上一篇文章，与传统的Block-Unblock编码孔径（CA）不一样，本文提出了一种带颜色的编码孔径（CCA），使得采样结果与波长有关，从而降低混叠图像的相关性，能有效提高欠定问题的求解精确性，并且能实现尽可能少的快照拍摄次数来往成重建工作。

下图显示了传统的编码孔径和颜色编码孔径的对比：

image-20201219195620028

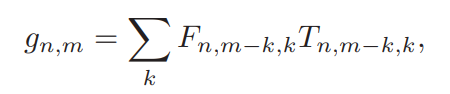模型还是如此：image-20201219195643587，从而，有这么一个公式可以表示数据立方体的第$k$个光谱带 和 第$l$次快照使用的编码孔径的任意点的数据：image-20201219195748065

显然：$j-\lfloor\frac{j}{N}\rfloor N = j \mod N$，所以上式是展示 第$j$个数据对应的行和列

色散效果对应的矩阵是一个 $N(N+L-1)\times N^2L$ 的矩阵，如下：

image-20201219200339487

编码孔径对应一个 $T_{(N^2L\times N^2L)}$ 的对角阵，对应每个元素是否被block，将$\mathbf P$与$\mathbf T$相乘，得到如下采样矩阵：

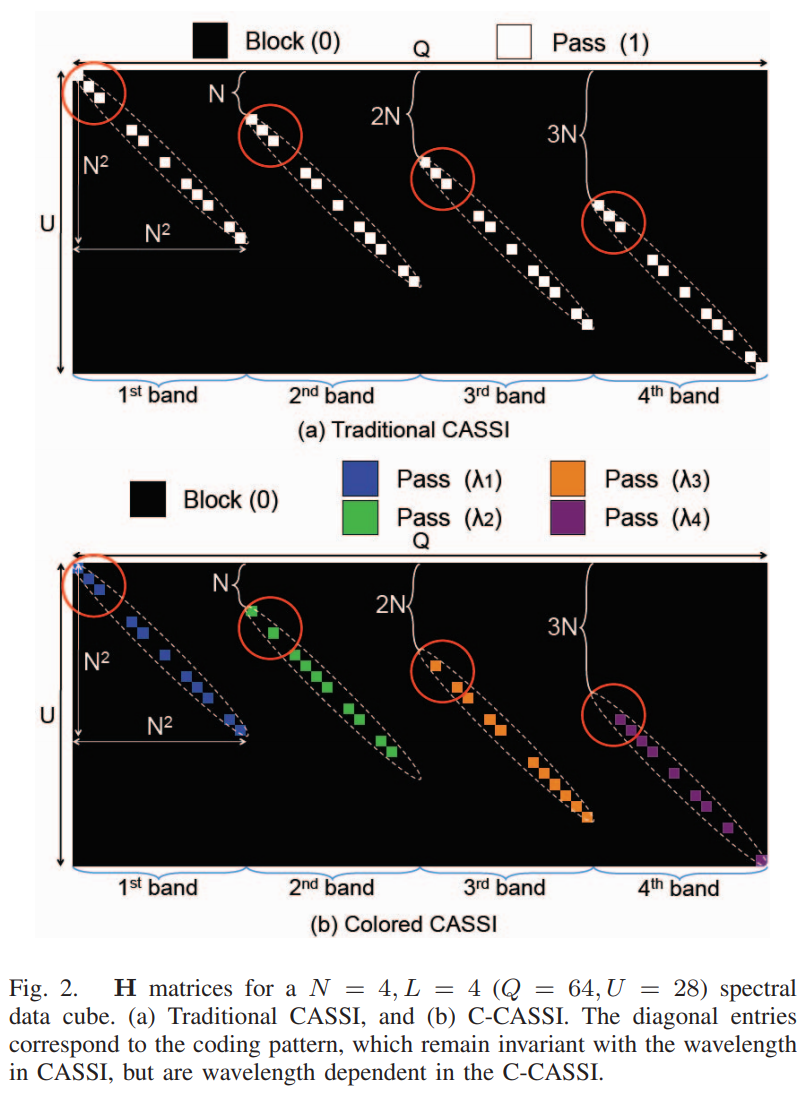
image-20201219200457907

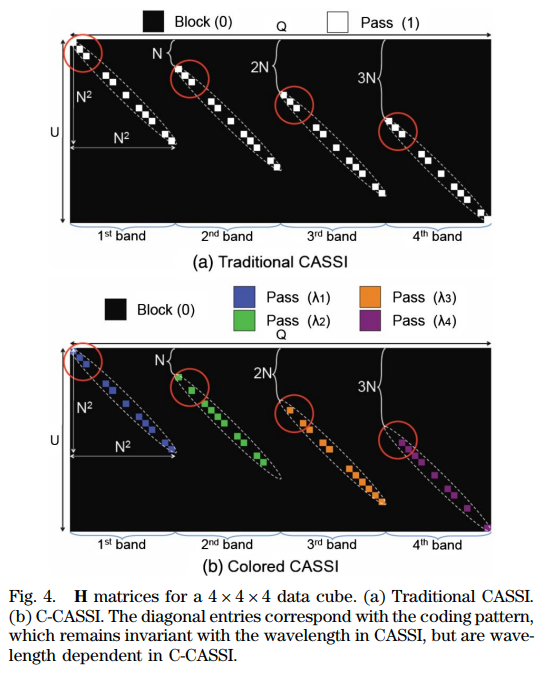
上图是传统CA与CCA的对比图，可以发现：

  • CA对应的矩阵每一个光谱段编码模式相同，而CCA每一个光谱段编码模式不相同

这是有利于欠定问题的解决的。

为了实现编码孔径的每个像素都能有2种及以上的滤光效果，作者制利用人造晶圆（Fabricated wafer）制作了这样的编码孔径，如下图所示：

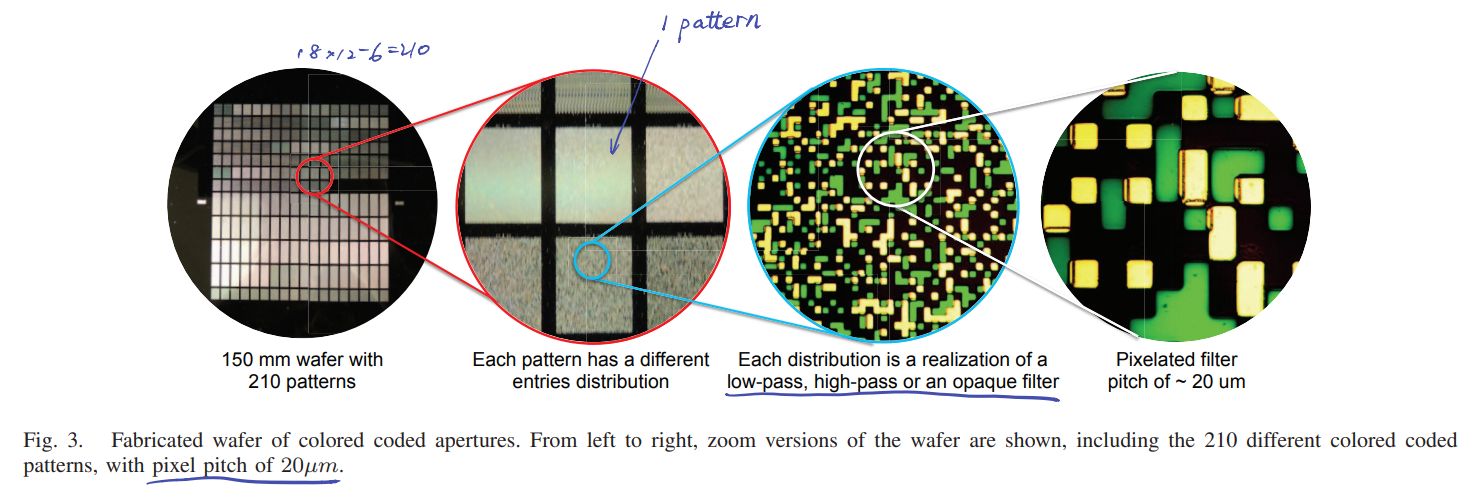
image-20201219201831957

最左侧显示了晶圆上的210个不同的编码孔径，每个编码孔径的编码模式不同，且都由低通和高通滤光片（尺寸约20$\mu m$）组成。

优化问题还是这样一个问题：

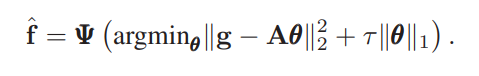
image-20201219202009172

Experiments

FPA传感器像素大小 $7.4\mu m$，分辨率 $2048\times 2048$，用一个$3\times3$的super-pixel 窗口来匹配FPA与编码孔径大小（因为CA中的滤光片尺寸约$20\mu m\approx3\times 7.4\mu m$），采用GPSR优化算法。

Results

快照数 K=1、K=6 对比：

image-20201219204128637

与原RGB图对比：

image-20201219204215181

Paper 4

Title

《基于DMD的模板滤光片阵列压缩光谱成像》

Rueda H , Arguello H , Arce G R . DMD-based implementation of patterned optical filter arrays for compressive spectral imaging[J]. Journal of the Optical Society of America A Optics Image Science & Vision, 2015, 32(1):80-9.

Contents

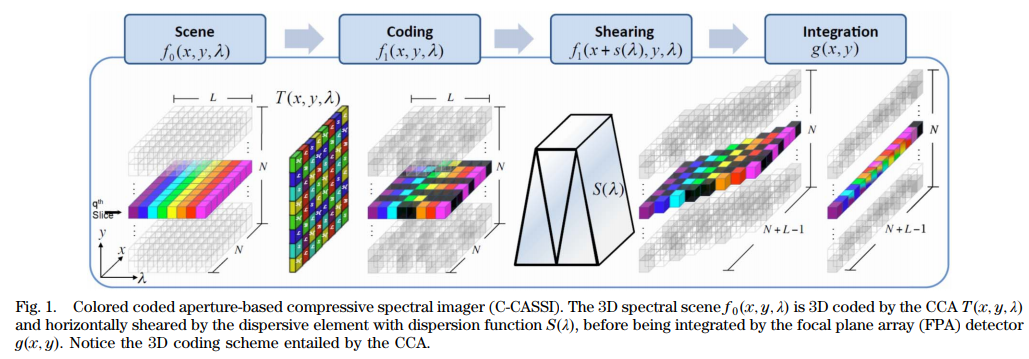
本文采用模板滤光片阵列取代传统的编码孔径，也就是彩色编码孔径CCA，它不仅可以调制空间维度，还可以同时调制光谱维度。

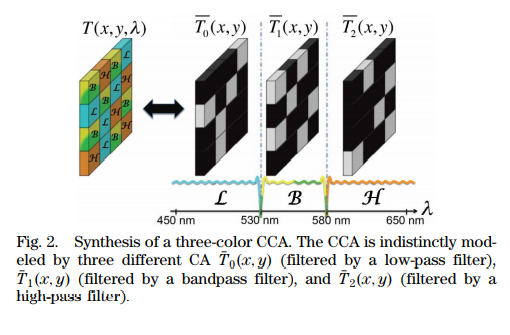
本文采用三种不同的滤光片L、H、B，分别对应着 低通滤波、高通滤波、带通滤波，采用DMD外接一系列滤光片实现，模型如下图：

image-20201219213617854

能够实现如下图类似彩色编码孔径的效果：

image-20201219213829422

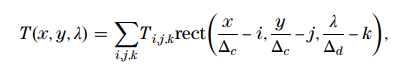
传统的数学模型：image-20201219213920606

由于 编码孔径影响的是空间分辨率，而FPA和色散影响的是光谱分辨率，所以作者将其改写成下式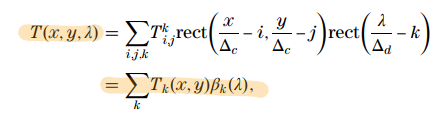：image-20201219214011117

对于本文，数学模型需要改一改，因为不同的编码孔径滤过的光谱段是不同的：

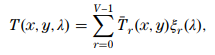
image-20201219214204867

其中，$\bar T_r(x,y)$ 对应三种波长响应不同的滤波器的block-unblock情况，于是成像问题就可以形象地用下图呈现：

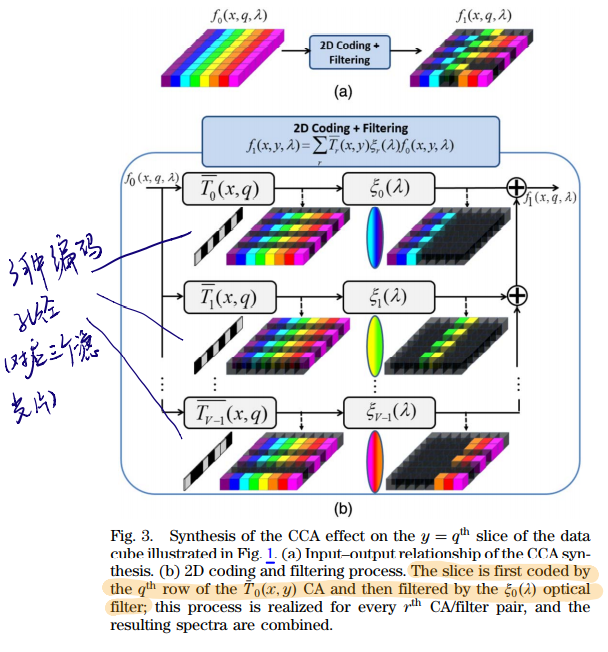
image-20201219214622998

定义CCA的透过率为

对于离散化的模型，传统模型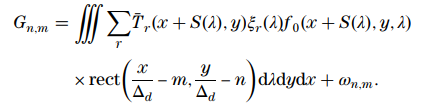：image-20201219214817396

而本实验模型为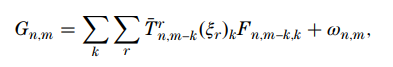：image-20201219214850334

其中，$(\xi_r)_k\in[0,1]$ 代表第$r$个滤光片阵列对于第$k$个光谱带的响应

作者给出了与前面文献相同的坐标表示法、P矩阵和测量矩阵：

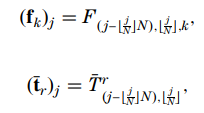
image-20201219215051907

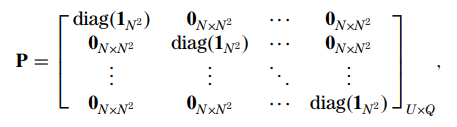
image-20201219215101843

image-20201219215125222

Experiments

Simulation

实验用氙气灯作光源，光谱 450nm~650nm，灰度CCD相机 $\Delta_d = 9.9\mu m$ 8位强度值，数据立方体尺寸 $256\times 256 \times 8$

实验用CA和CCA的透过率基本固定在50%，都采用伯努利随机分布，$p=0.1-0.8$

CCA的滤光片种类设置为（ 2种、4种、8种 ）这三种情况

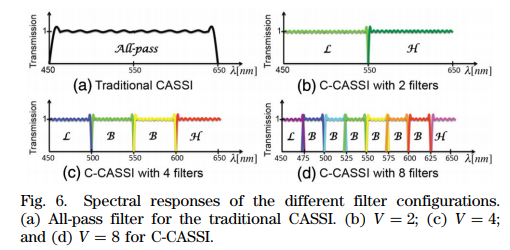
image-20201219215715235

将FPA的像素尺寸和CCA、CA的像素尺寸都设置为$256\times 256$，以完成匹配

采用GPSR优化算法求解最小二乘，系数基是 二维小波变换 乘 离散余弦变换，快照数量$K=1,2,…,8$

Results

实验表明 R=0.2、0.3 时重建效果最好，并得出一个大致结论：

  • $R\approx 1/K$ 时结果更优

image-20201219220207992C-模拟

image-20201219220605180

模拟结果显示：

  • V（滤光片种类）越多，效果越好
  • K（快照次数）越多，效果越好，因为每次快照是用的不同的编码模板，信息更多

Experiment setup

作者真实实验设备的搭建如下，其中滤光片阵列是加在一个圆盘上

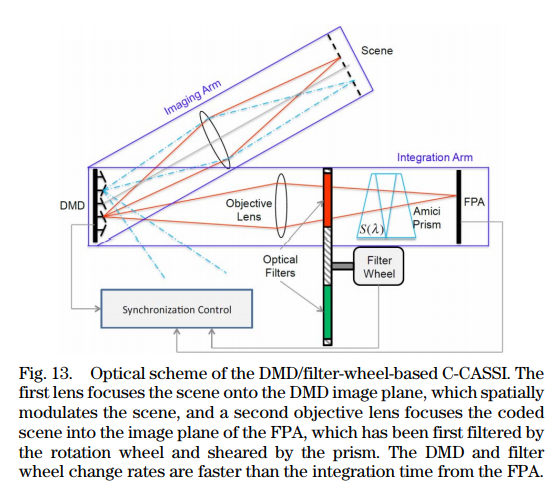
image-20201219220708339

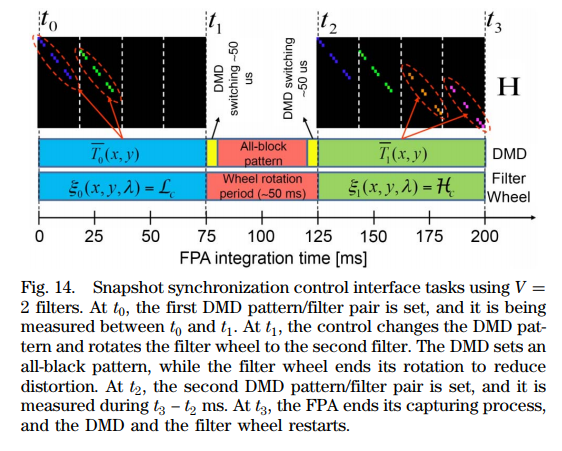
需要有一个同步控制系统控制DMD、转盘、FPA的交替同步成像，如下图所示

image-20201219220820311

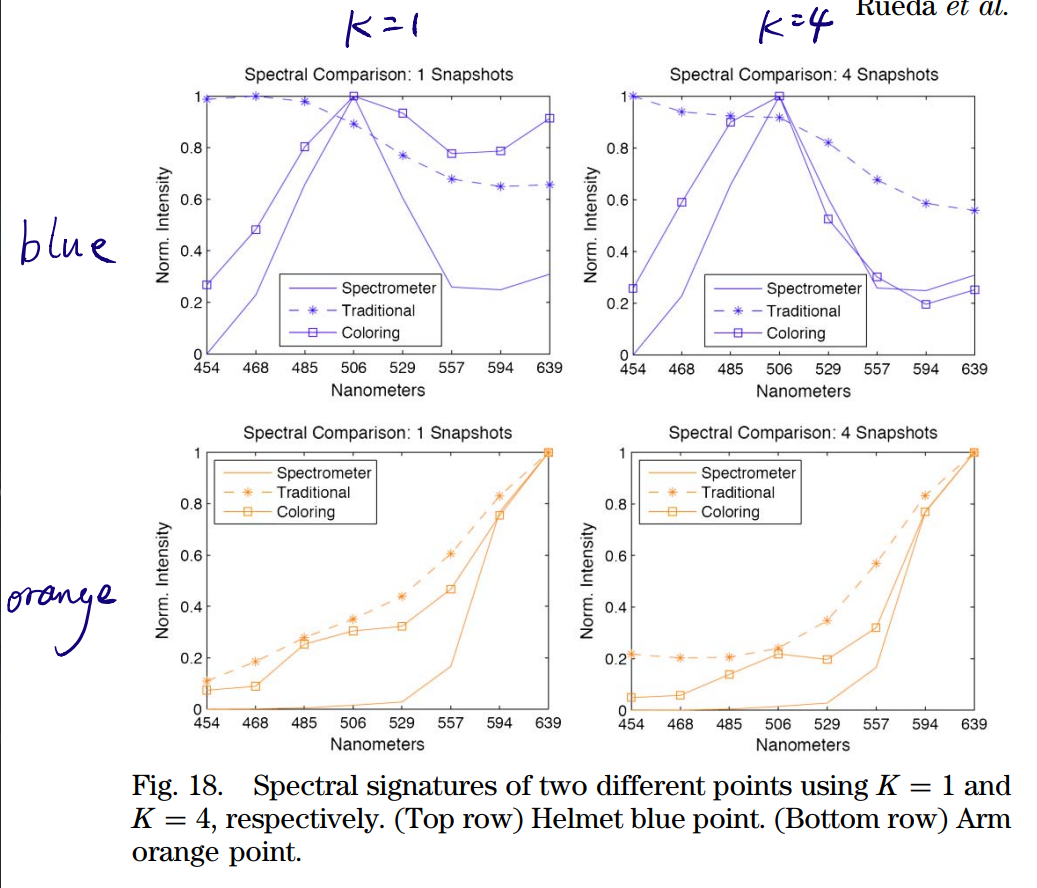
Results

实验结果表明：

  • 传统的CA成像结果会产生更多像素聚集在一起的情况，而CCA成像像素分布更加均匀

image-20201219220900527

image-20201219220926004

image-20201219220951289

项目记录
周报

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！