周报：2020-12-7~2020-12-13

本周主要研读了以下内容：

  • 中科院大学的刘铭鑫博士 的博士学位论文《基于压缩感知的编码孔径光谱成像技术研究》
  • Arguello, H, Carin, et al. Compressive Coded Aperture Spectral Imaging: An Introduction[J]. IEEE Signal Processing Magazine, 2014.
  • Galvis L , Arguello H , Arce G R . Synthetic coded apertures in compressive spectral imaging[C]// 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2014.
  • Galvis L , Arguello H , Arce G R . Synthetic coded apertures in compressive spectral imaging: Experimental validation[C]// 2015 IEEE Global Conference on Signal and Information Processing (GlobalSIP). IEEE, 2016.

同时，实现了CoSaOMP算法（压缩采样匹配追踪），发现确实比OMP重建效果好，但用时更长。

CASSI 系统

双色散型光谱维编码

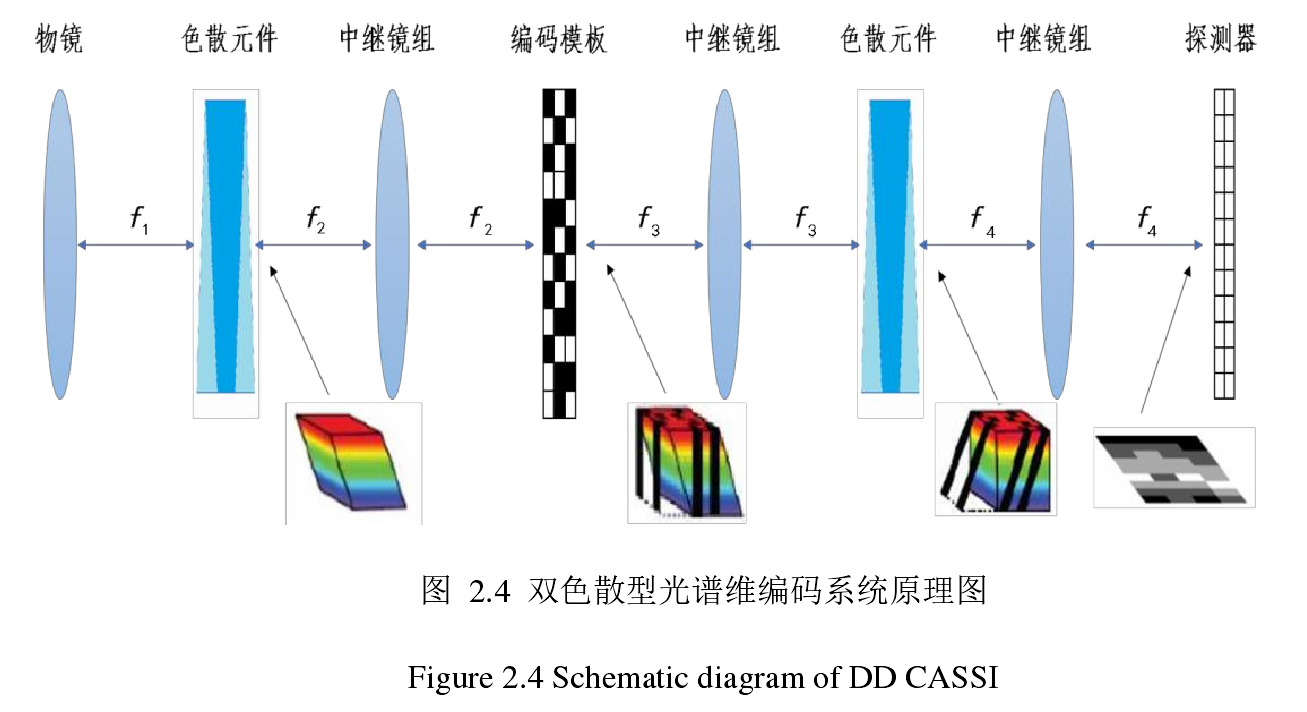
image-20201212150504924

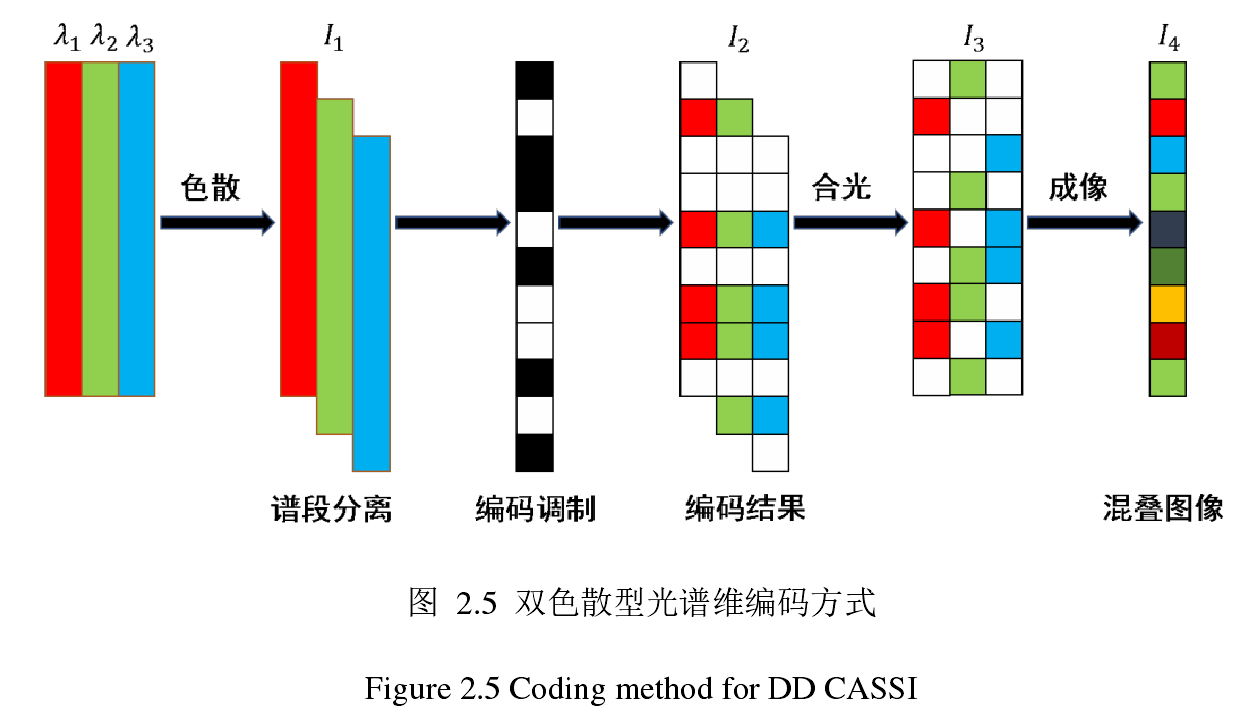
image-20201212145728927

如图所示，数据立方体首先经过色散分光，然后经过一个编码孔径进行调制，得到调制后的数据，随后再反色散分光（目的是为了将shearing过的数据恢复成初始的立方体，称为合光），最后投射（沿光谱维度积分）在探测器上

合光后的数学表示为

可以发现，本质上可以这么理解：数据立方体的每一个光谱段的空间信息都被不同地过滤了。

  • 补充说明：如果色散作用是使得两相邻光谱沿$x$坐标轴正向错开一个像素单位，那么数据立方体中的第一个光谱段空间信息并没有被错开，等效于它被原始的编码孔径过滤了，但从第2个开始就不一样了，假设现在观察的对象为第$i$个光谱段的空间信息，发现其实它相对于第1个光谱段 在$x$轴正向错开了$(i-1)$个像素单位，等效于 它被原始编码孔径在沿$x$轴负向错开$(i-1)$个像素单位之后得到的编码孔径过滤了，依此类推，所以数据立方体的每一个波段信息都不同，称为光谱维编码
  • 因此，编码孔径的长度应该是 $空间维度尺寸 + 光谱维度尺寸 - 1$，而探测器尺寸应该为 $空间维度尺寸$

最终透射在探测器上的数学表示为

单色散型空间维编码

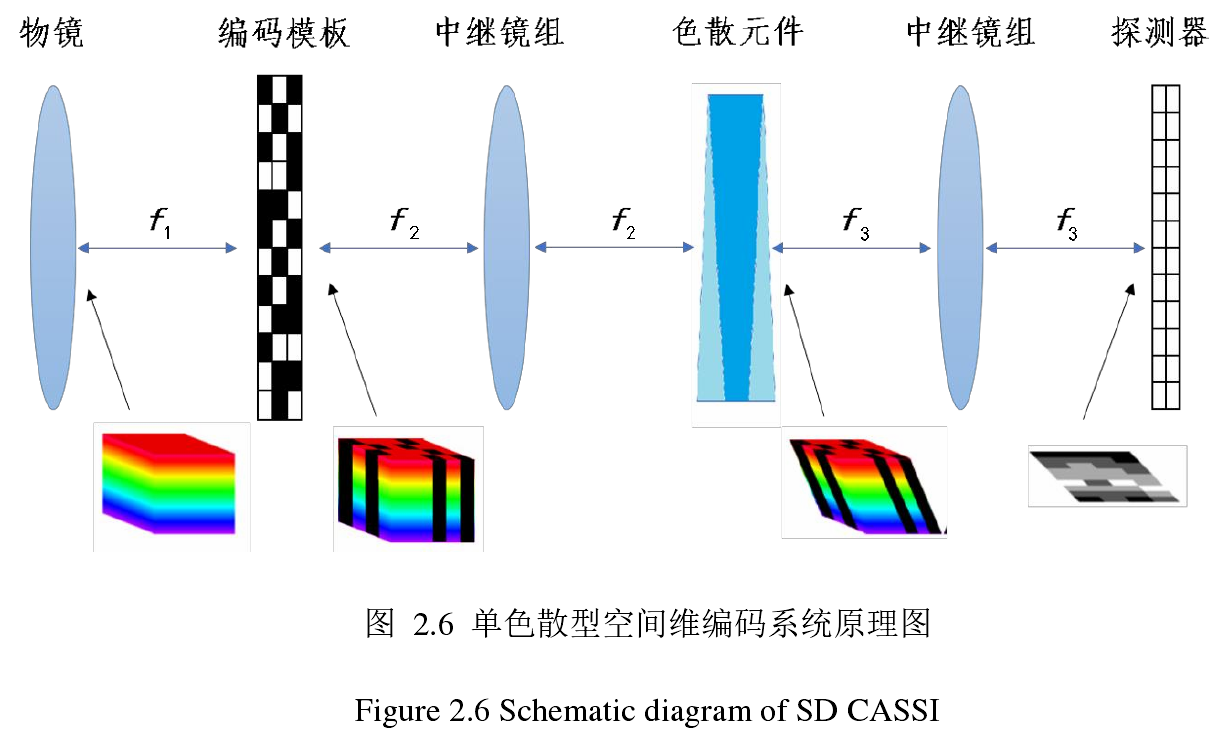
image-20201212150911819

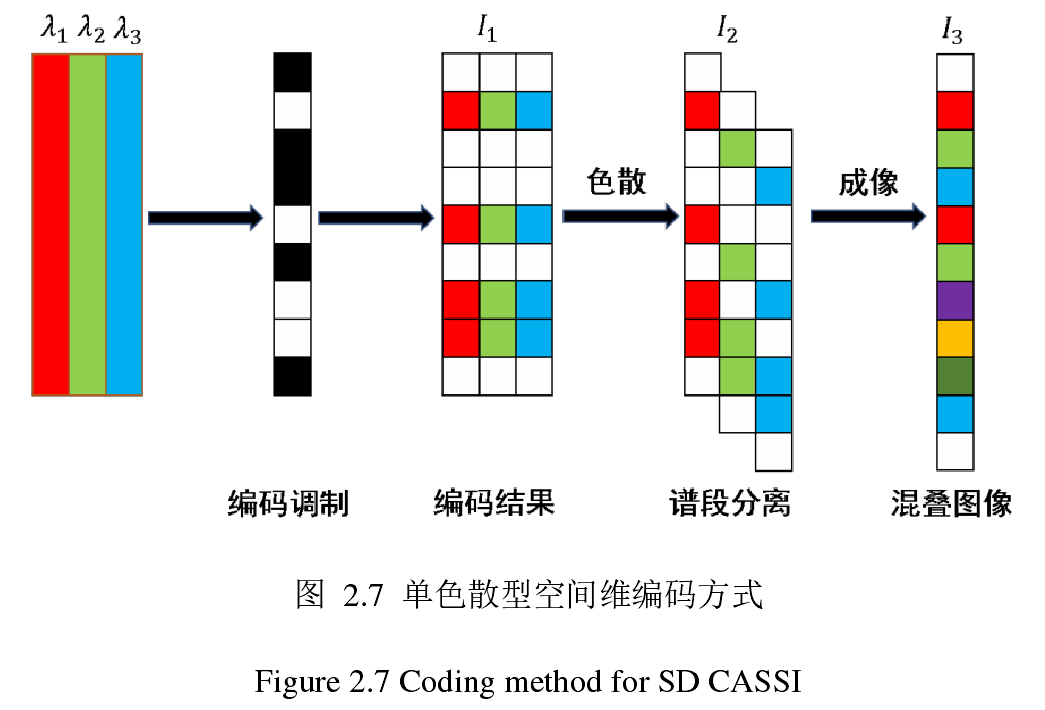
image-20201212152144119

数据立方体首先经过编码孔径调制（此时所有光谱维度的空间信息都被相同的无差别过滤了），然后再色散分光，最后投射到探测器上

探测器前的光谱信息数学表示为：（得到光强信息，只需要对下式在波长上积分）

  • 因此，编码孔径的尺寸与数据立方体空间尺寸相同，而探测器尺寸应该为 $空间维度尺寸+光谱维度尺寸-1$

最终投射在探测器上的光强为

探测器像元离散化

由于真实情况下，所有探测器获取的数据都是离散化的结果（对应探测器的像元信息），因此需要对上面讨论的方程进行离散化建模

考虑单色散型空间维编码，设 探测器像元尺寸为 $\Delta d$，系统噪声为 $\sigma$，那么对于探测器像元$(i,j)$而言，它所获取的光强可以表示为：

这个式子表明：一个像元上的光强 是 对应像元位置的连续空间位置的光谱信息的叠加

这里补充解释一下，看下图：

image-20201212170350356

  • 我从其他文献中（Galvis L , Arguello H , Arce G R . Synthetic coded apertures in compressive spectral imaging: Experimental validation[C]// 2015 IEEE Global Conference on Signal and Information Processing (GlobalSIP). IEEE, 2016.），也看到了类似的式子，想表达的意思是相同的。图中红线部分的矩形函数用来表示对应坐标的像元矩形，张量积的意义就是把对应行列的向量做张量积，最终的结果也是对应的像元矩形，所以矩形函数的存在把积分限限制在了对应像元内部。

  • 那么上式的意义就很明了了：连续函数$g$ 对像元对应位置的矩形内元素进行积分，也就是像元内光谱信息的累加，我改写为下式，就很好理解了

数字微反射镜（Digital Micromirror Device, DMD）

DMD是一种常用的空间光调制器（Spatial Light Modulator, SLM），它是由多个高速数字式光反射开关组成的阵列，一个小镜片对应一个像素，相对于TFT-LCD（液晶）的透射率低，对比度小，DMD的反射率高，对比度大。结合光源和光学器件，DMD可以实现在速度、精度和效率上远超其他空间光调制方式的二进制图形。DMD的每个镜片都可以分别围绕铰接斜轴进行 +/-12° 的偏转，镜片的偏转是通过更改底层CMOS控制电路和镜片复位信号的二进制状态进行单独控制的，从而使其可以在DLP投影系统倾向光源（打开）或背离光源（关闭），在投影表面造成像素的或明或暗。

通过研读文献，了解到编码孔径的大多都是采用DMD实现的，通过编程设置镜片偏转实现布尔类型的编码孔径。

Paper 1

Title

《合成编码孔径压缩光谱成像》

Galvis L , Arguello H , Arce G R . Synthetic coded apertures in compressive spectral imaging[C]// 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2014.

Contents

通常情况下，Brady等人创造出的，传统的基于编码孔径的压缩感知光谱成像系统（CASSI）常常会出现 编码孔径像素 与 焦平面探测器像素 不匹配的问题，如下图所示：

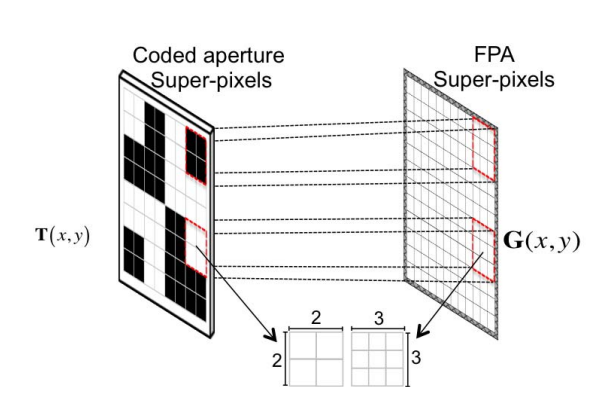
image-20201213203511359

传统的解决方案是设置一个 super-pixel 如上图所示，将编码孔径的$2\times 2$个像素与FPA的$3\times 3$个像素匹配起来，整体当成一个“超级像素“来处理，这样的处理方式显然会造成最终成像结果的空间分辨率和光谱分辨率低下的问题，本文提出了一种新型处理方式，通过人工合成一种编码孔径，将原始编码孔径设置的值通过数学建模的方式映射到新的合成编码孔径上，这种编码孔径的像素大小与FPA像素大小一致，因此不需要采用 super-pixel，分辨率大大提高。

传统模型如下：

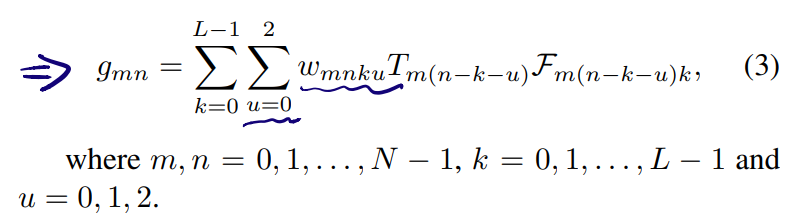
image-20201213204224336

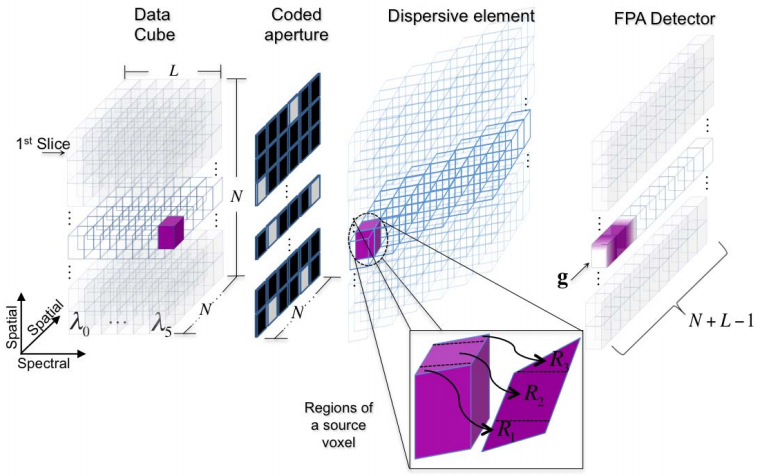
​ image-20201213204251220

需要注意的是，作者采用的是单色散型编码模式，因此最终投影到FPA上的是一个经过色散的倾斜的数据立方体，这里作者将其划分为三个部分，因此上式多了一个求和号（u）

新的合成编码孔径模型示意图如下：

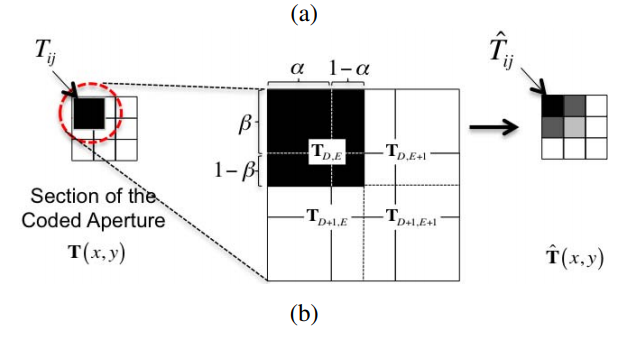
image-20201213204554520

以 $\Delta_d:\Delta c = 2:3$ 为例，作者将$2\times 2$的原始孔径与新孔径做对比，显然原始孔径一个pixel的值会贡献到新孔径的相邻几个部分，如上图所示，右侧的图的深浅表示了其中一个原始像素对各个新像素点的贡献大小，这里作者用了一段我看了整整两天都没看懂的公式描述了这一点：（这个式子确实有点迷，但意思作者写的很明白了）

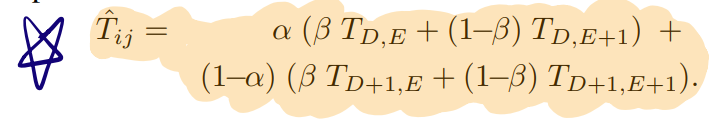
image-20201213204846612

最后，抛出最终的新模型：

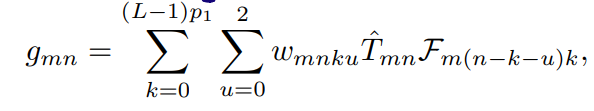
image-20201213205030668

需要注意的是，上式第一个求和号上限乘了一个$p_1$（即一个超级像素的尺寸与一个FPA像素尺寸之比），这么写直观上是光谱维度数据变密了，是原来的$p_1$倍，感觉是因为 像素点变多了（因为编码孔径$\Delta_c$变小了），因此色散产生的光谱数据遍多了。

Experiments

实验中FPA尺寸为$384\times 384$，光谱段数为24，单色仪采样了$450-650$之间的波段，探测器为CCD相机AVT Marlin F0033B，有$656\times 492$个像素，每个像素尺寸为$9.9\mu m$。作者分别做了25%和50%透过率的两种编码孔径做对比实验，编码孔径分辨率为$256\times 256$，所以显然与FPA分辨率比值为$2:3$。

所需重建的问题是 优化一个带有L1正则化的最小二乘，采用了GPSR（梯度投影稀疏重建法）算法，稀疏基采用 8 basis二维小波变换矩阵 与 一维离散余弦变换 的克罗内克积，最终成像结果为一个$384\times 384 \times 24$的数据立方体。

Results

image-20201213210455048

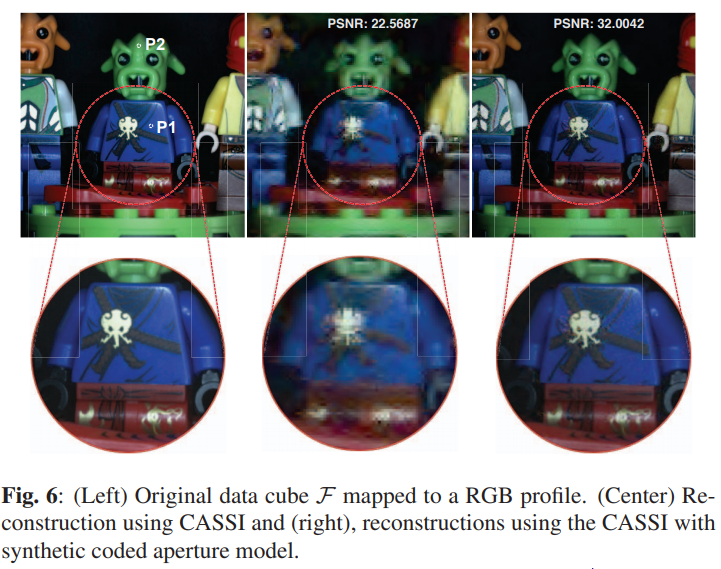
image-20201213210530309

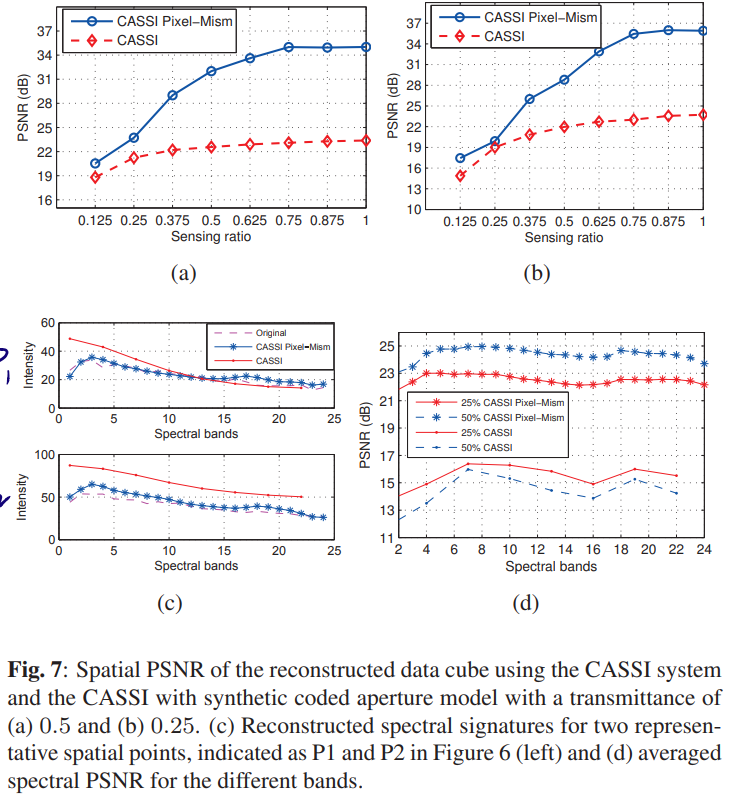
image-20201213210600925

Paper 2

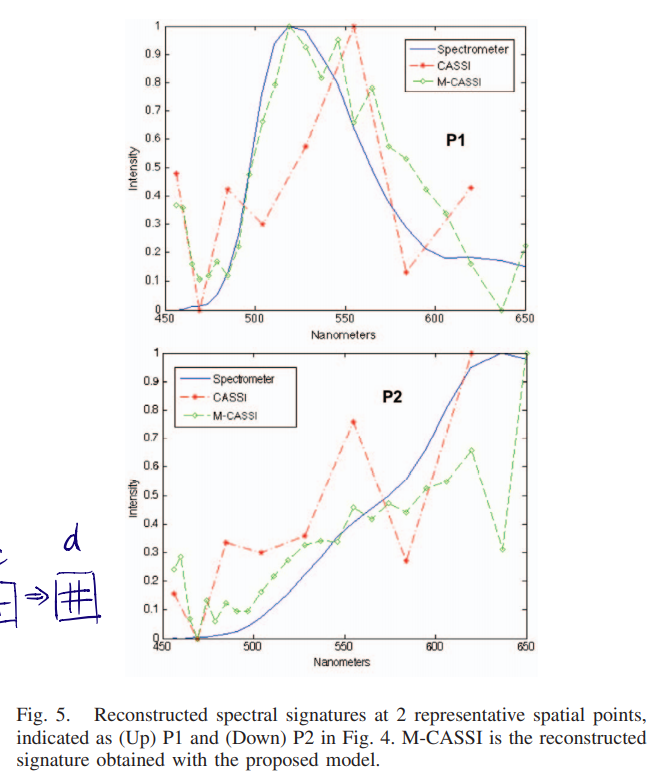
这篇文章是上一篇文章的实验验证部分， 对比了传统的CASSI方法和合成编码空间方法的重建结果，表明新方法显著的优势。

PS：我发现它更加详细地解释了理论模型部分。

结果如下方图片所示：

image-20201213210930571

image-20201213210946473

CoSaOMP 算法实现

下图是稀疏系数k不同时的重建结果

B_Different_k

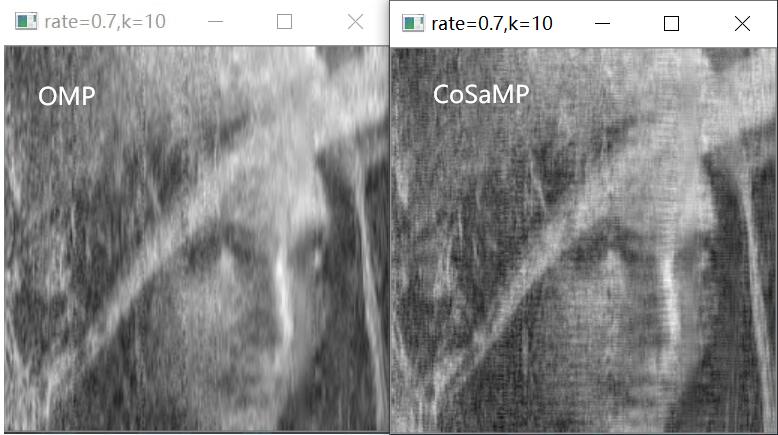
下图是OMP与CoSaMP在相同条件下的对比

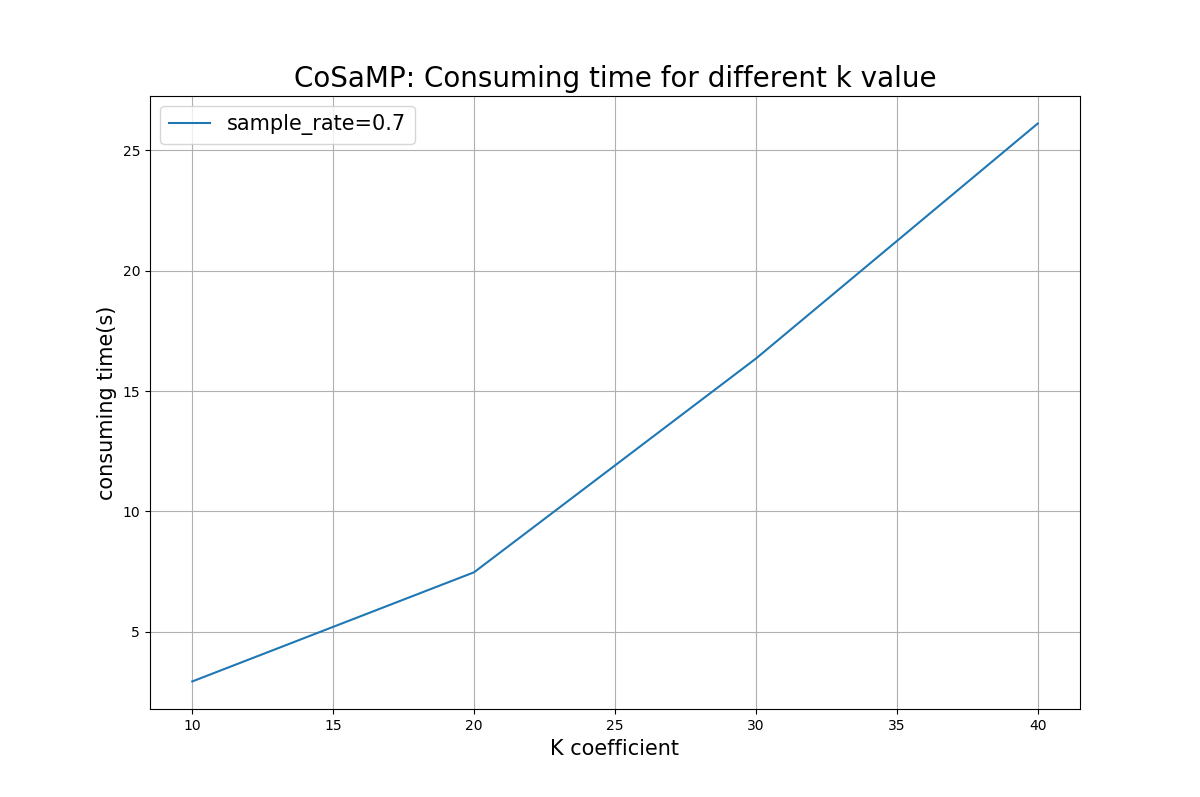
下图是CoSaMP算法在不同稀疏稀疏k取值下的重建时间

test1

code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
import random
import numpy as np
import time
import sys
import cv2
import matplotlib.pyplot as plt
import scipy.optimize as spopt
import scipy.fftpack as spfft
import scipy.ndimage as spimg

# Compressive Sampling Matching Pursuit algorithm
def OMP(y,A,K):
	col = A.shape[1]
	residual = y
	ind = np.array([],dtype=np.int64)
	Res = np.zeros((col))
	for i in range(K):
		prod = np.fabs(np.dot(A.T,residual))
		ind = np.union1d(ind, np.argsort(-prod)[:2*K])
		tmp = np.zeros((256))
		tmp[ind] = np.dot(np.linalg.pinv(A[:,ind]),y)
		pos_tmp = np.argsort(-np.fabs(tmp))[:K]
		Res[pos_tmp] = tmp[pos_tmp]
		residual = y-np.dot(A,Res)
	return Res

img = cv2.imread("lena.jpg")
img = img[128:128+256, 128:128+256, 0]

# cv2.imshow("img",img)
# cv2.waitKey(0)

# radom gaussian matrix ----> undersample
sample_rate = 0.7
N = 256
Phi = np.random.randn(int(sample_rate*N),N)
Phi /= np.linalg.norm(Phi)

# plt.imshow(Phi)
# plt.colorbar()
# plt.show()
# exit(0)


# DCT matrix ----> sparse base
Psi = np.zeros((N,N))
n = np.array(range(N))
for k in range(N):
	Psi[k,:] = (2/N)**0.5*np.cos((2*n+1)*k*np.pi/2/N)
Psi[0,:] /= 2**0.5
Psi = Psi.T

# plt.imshow(Psi)
# plt.colorbar()
# plt.show()
# exit(0)


# measurement ----> undersample image
measure_mat = np.dot(Phi,img)

# K coefficient for N colomns
sparse_coe = np.zeros((N,N))

# θ = Φ ψ
Theta = np.dot(Phi,Psi)


time_consume = []
# OMP for every colomn
for k in range(10,25,5):
	st = time.perf_counter()
	for i in range(N):
		sparse_coe[:,i] = OMP(measure_mat[:,i],Theta,k)
	en = time.perf_counter()
	img_rec = np.dot(Psi,sparse_coe)
	img_rec /= img_rec.max()
	img_rec *= 255
	img_rec = img_rec.astype(np.uint8)
	# print(img_rec.shape)
	# print(img.shape)
	# cv2.imshow("img",img)
	sys.stdout.writelines(f"rate={sample_rate:.1f},k={k} runtime:{en-st}s ")
	time_consume.append(en-st)
	mse = np.sum((img_rec-img)**2)/256/256
	PSNR = 10*np.log10(np.max(img_rec)**2/mse)
	sys.stdout.writelines(f'PSNR = {PSNR}dB\n')
	img_rec = cv2.putText(img_rec,f"PSNR={PSNR:.0f}",(20,20),cv2.FONT_HERSHEY_SIMPLEX,0.5,(255,255,255),1)
	cv2.imshow("rate=%.1f,k=%d"%(sample_rate,k),img_rec)
cv2.waitKey(0)



# sparse_coe[sparse_coe!=0] = 255
# sparse_coe = sparse_coe.astype(np.uint8)
# cv2.imshow("sparse_coe",sparse_coe)
# cv2.waitKey(0)

# plt.figure(figsize=(12,8))
# # plt.plot([i for i in range(256)],img[:,0])
# # plt.plot([i for i in range(256)],img_rec[:,0])
# # plt.legend(['origin','reconstruction'],fontsize=15)
# # plt.title('Reconstruction result for column 0 with sample_rate=%.1f'%sample_rate, fontsize=15)
# plt.plot([i for i in range(10,50,10)],time_consume)
# plt.xlabel('K coefficient',fontsize=15)
# plt.ylabel('consuming time(s)',fontsize=15)
# plt.title('CoSaMP: Consuming time for different k value',fontsize=20)
# plt.grid()
# plt.legend(['sample_rate=%.1f'%sample_rate],fontsize=15)
# plt.show()

项目记录
周报

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！