周报:2020-11-23~2020-11-29
这周的四篇论文,前三篇都是出自同一个团队,采用的方法类似,但侧重点不同
Paper 1
Title
《选取稀疏模板实现滤光片光谱仪光谱重建》
Chang C C . Spectrum reconstruction for filter-array spectrum sensor from sparse template selection[J]. Optical Engineering, 2011.
Contents
本文着重讲述了,在大规模的欠定线性方程组中,利用高斯曲线拟合整个光谱的方法,用吉洪诺夫正则化非负最小二乘方法实现比较合理的光谱重建
下图是文献核心算法部分

同时,本文详细介绍了吉洪诺夫正则化(通常为L2正则化)和L1范数正则化方法
Results
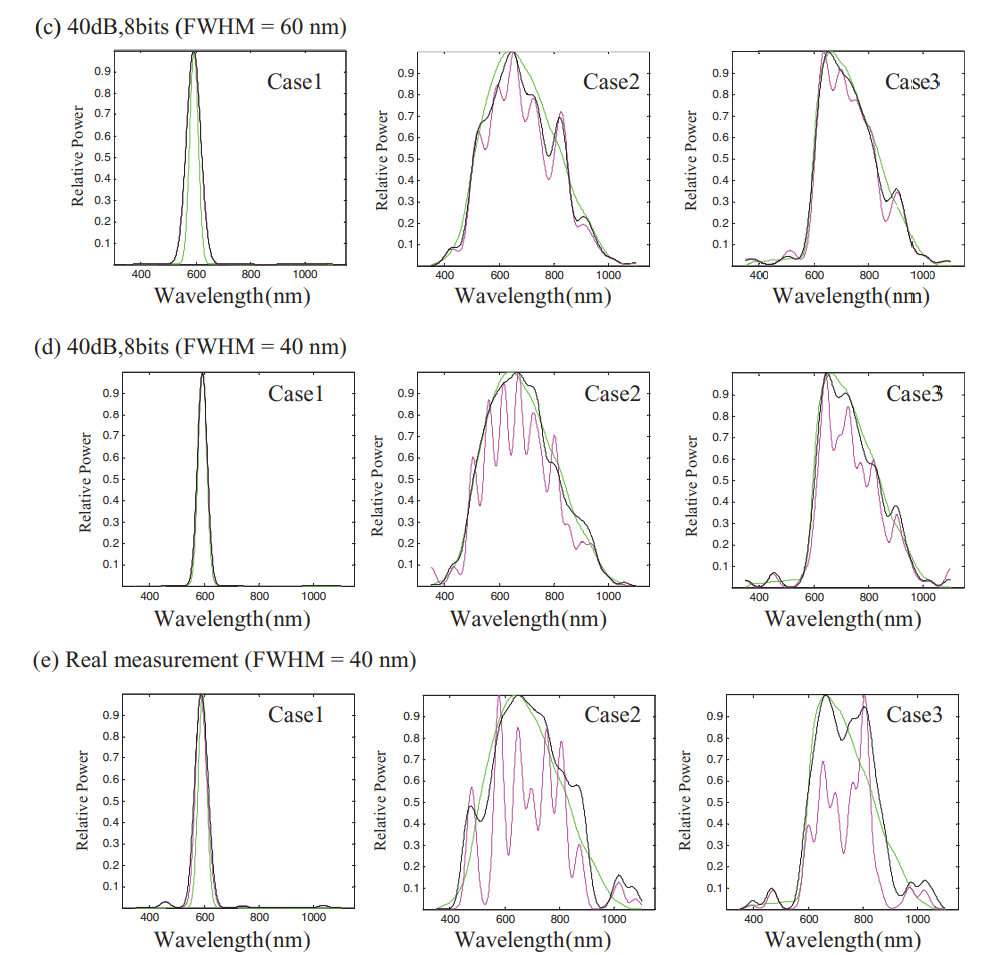
红线:NNLS;黑线:TNNLS;绿线:真值
黑线:L1正则化方法
Paper 2
Title
《基于光滤光片微型光谱仪的光谱重建自适应正则化方法》
Kurokawa U , Choi B I , Chang C C . Filter-Based Miniature Spectrometers: Spectrum Reconstruction Using Adaptive Regularization[J]. IEEE Sensors Journal, 2011, 11(7):1556-1563.
Content
本文着重于讲述了吉洪诺夫正则化参数的选取方法:L曲线方法和广义交叉验证法(GCV)
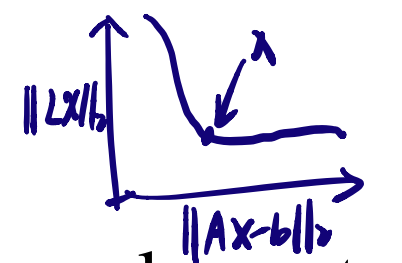
L曲线是类似与下图(我画的)的一种曲线,选取转折点为最优的正则化参数
本文提到了 zeroth-order、first-order、second-order 的吉洪诺夫矩阵,本文着重展示了zeroth-order中应用L曲线的优势
Results
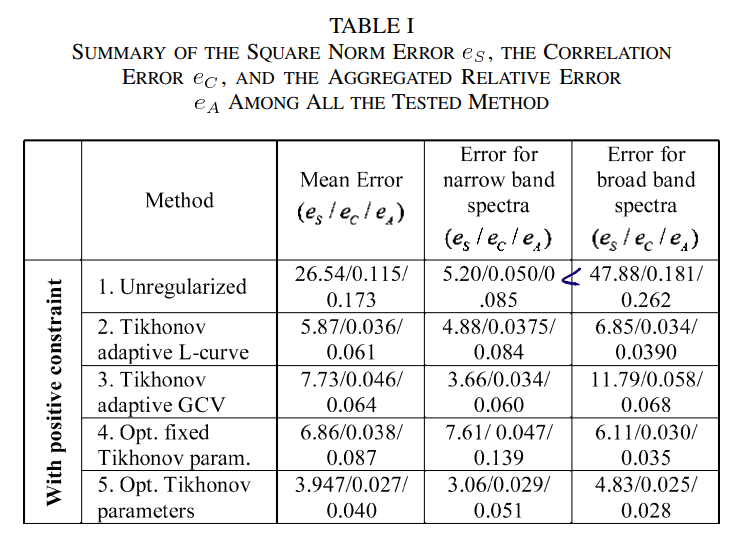
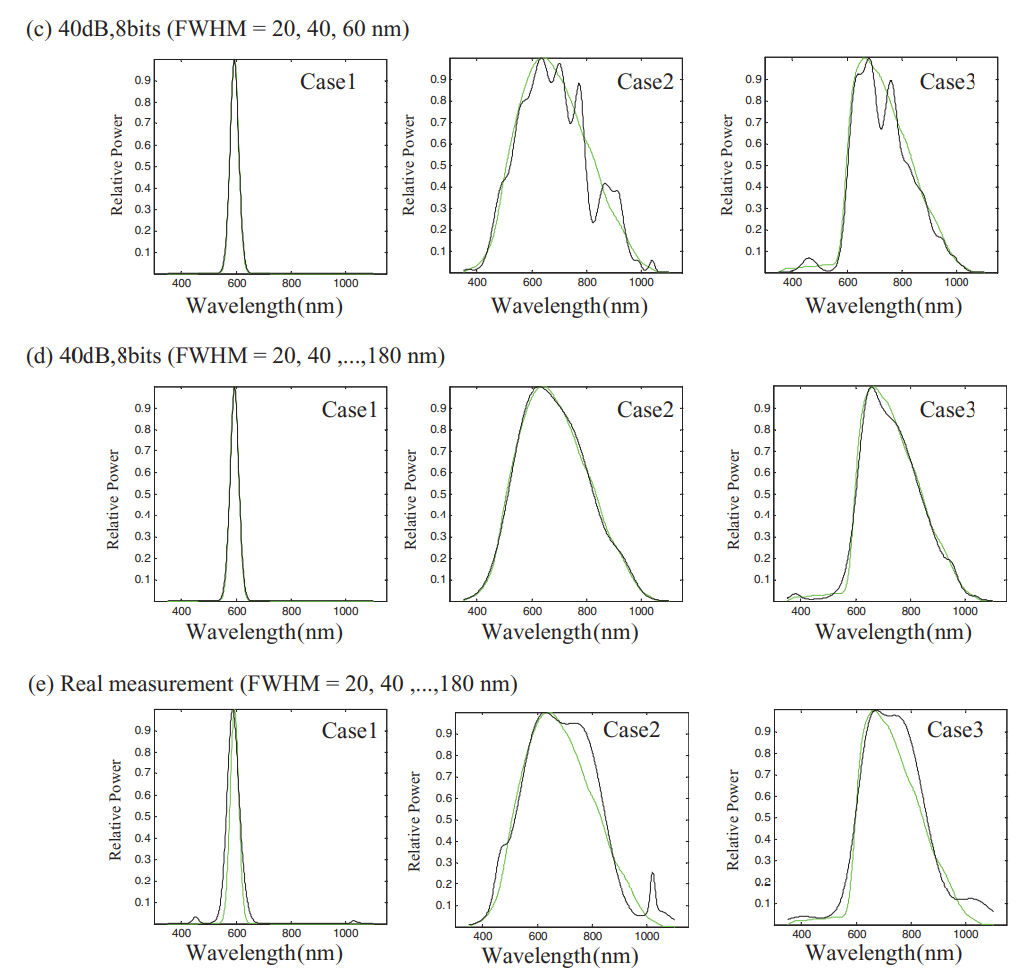
结果显示,窄带光谱比宽谱要好重建,同时,在零阶吉洪诺夫矩阵下,L曲线要明显好于GCV方法
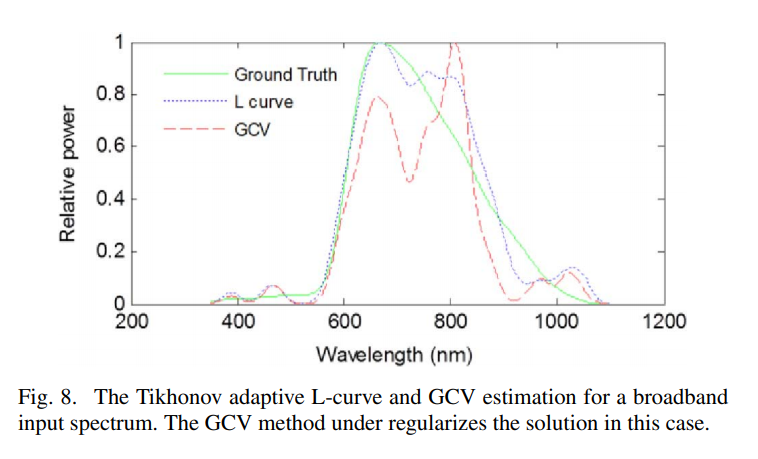
最后,附录还提供了zeroth-order、first-order、second-order 三种吉洪诺夫矩阵的所有对比实验结果,供读者参考,可以发现的是,有些情况下GCV表现得要比L曲线好很多。
Paper 3
Title
《芯片光谱仪光谱重建的新型非均匀性矫正算法》
Chang C C . Spectrum Reconstruction for On-Chip Spectrum Sensor Array Using a Novel Blind Nonuniformity Correction Method[J]. IEEE Sensors Journal, 2012, 12(8):2586-2592.
Contents
本章侧重于描述 入射光照射在不同色散传感器上的光强分布不均匀性 问题,因此提出了一个迭代算法用于修正入射光权值系数
对于本问题,数学模型需要在前部乘上一个权重系数,然后利用TNNLS算法解决重建问题
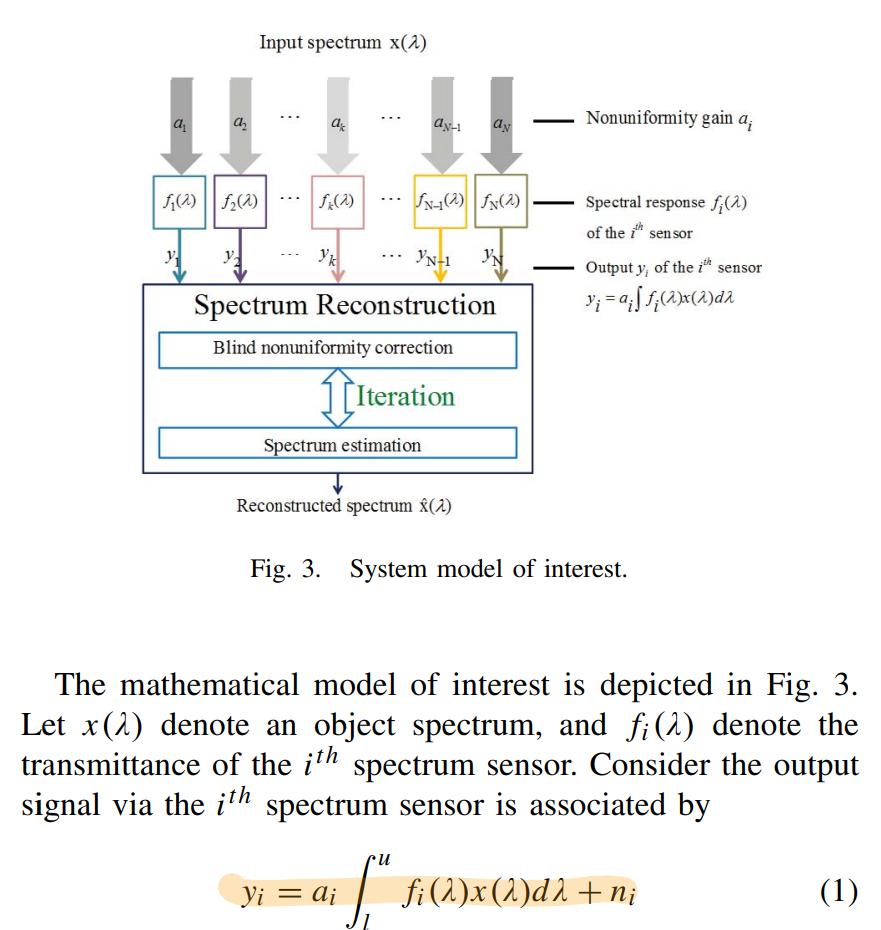
关键是修正权系数,算法流程如下,右侧是我写的证明算法收敛的笔记
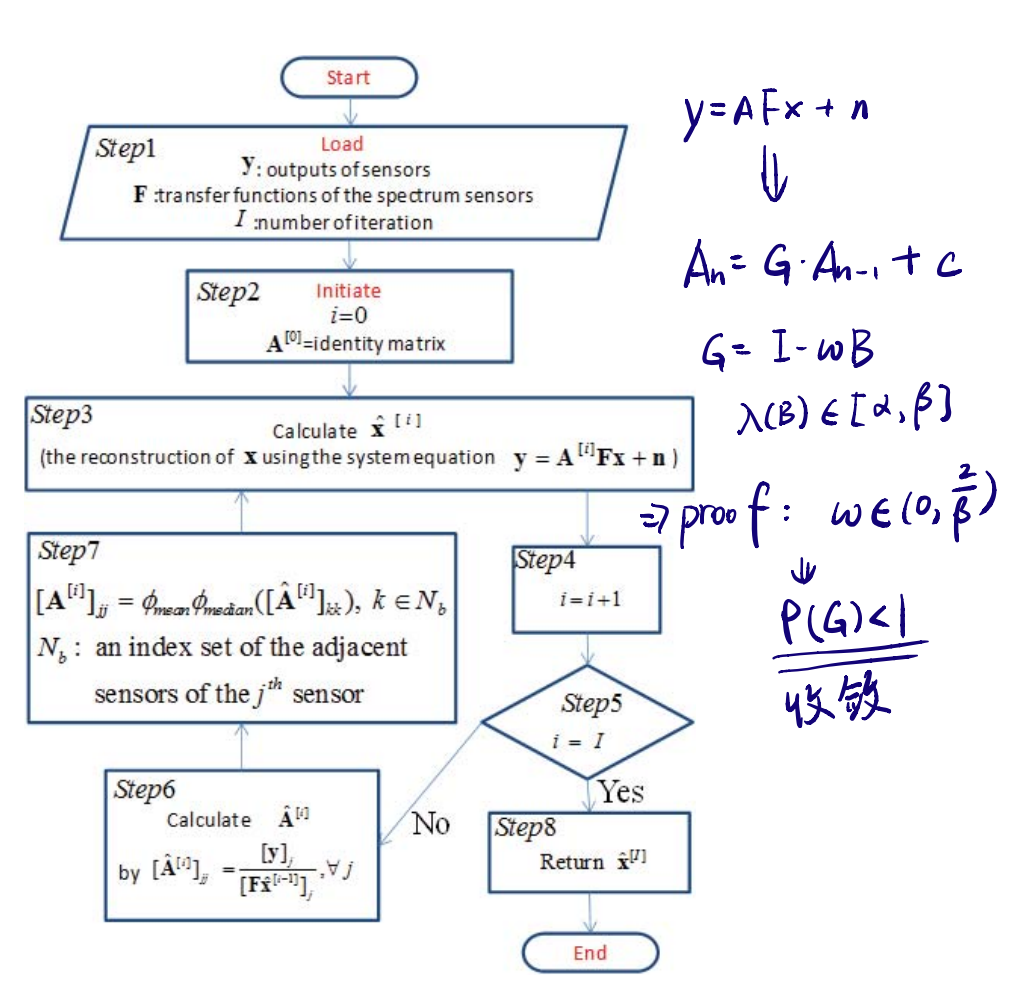
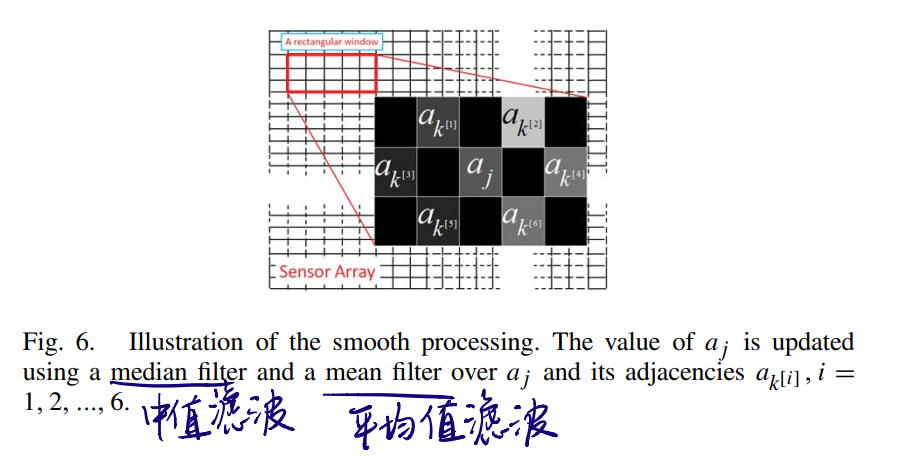
考虑到各种误差波动因素,所以需要对Setp6得出的A矩阵进行平滑操作,这里作者接了两个滤波操作(卷积)用来抹平噪声。
Results
左边是模拟,右边是实验
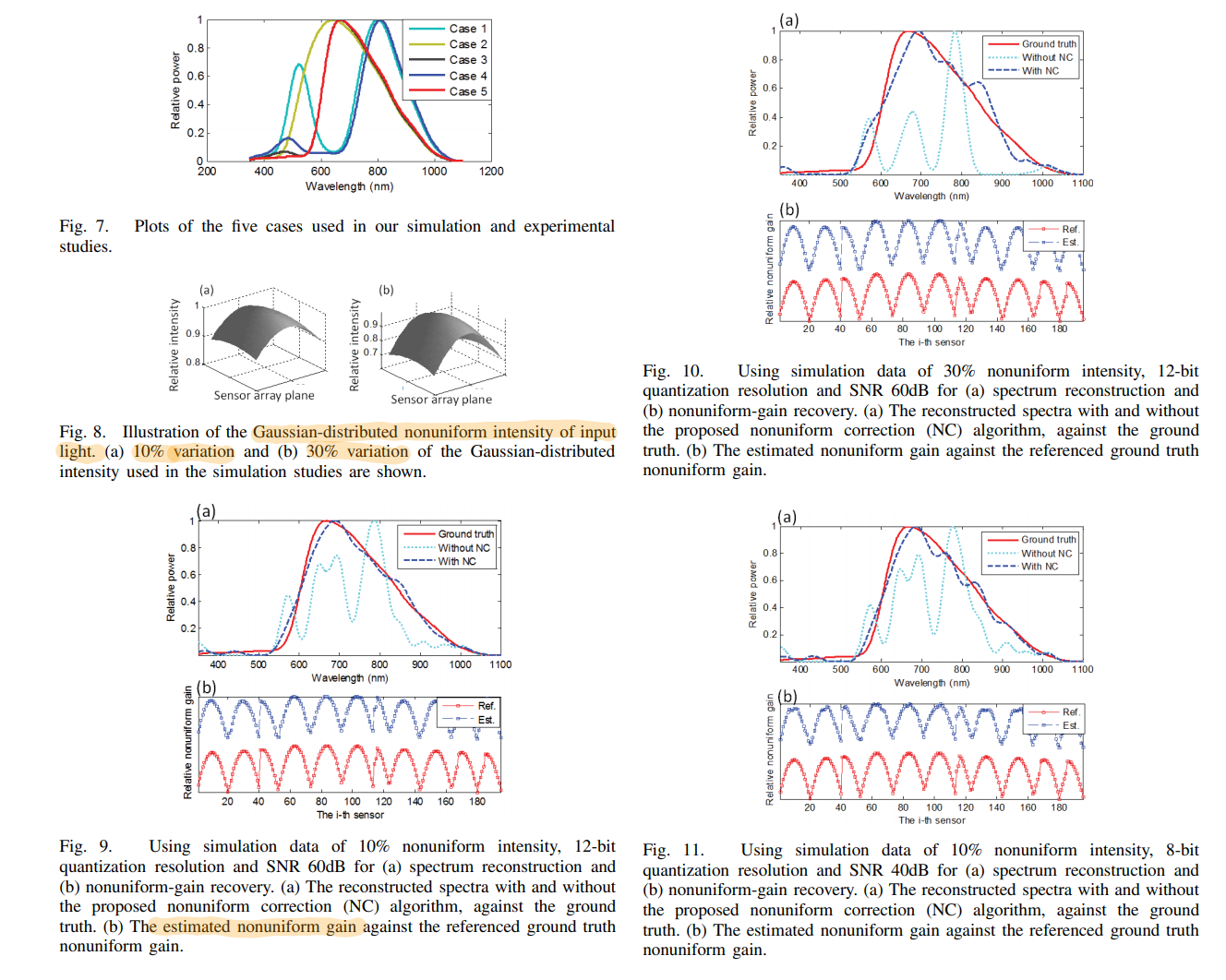
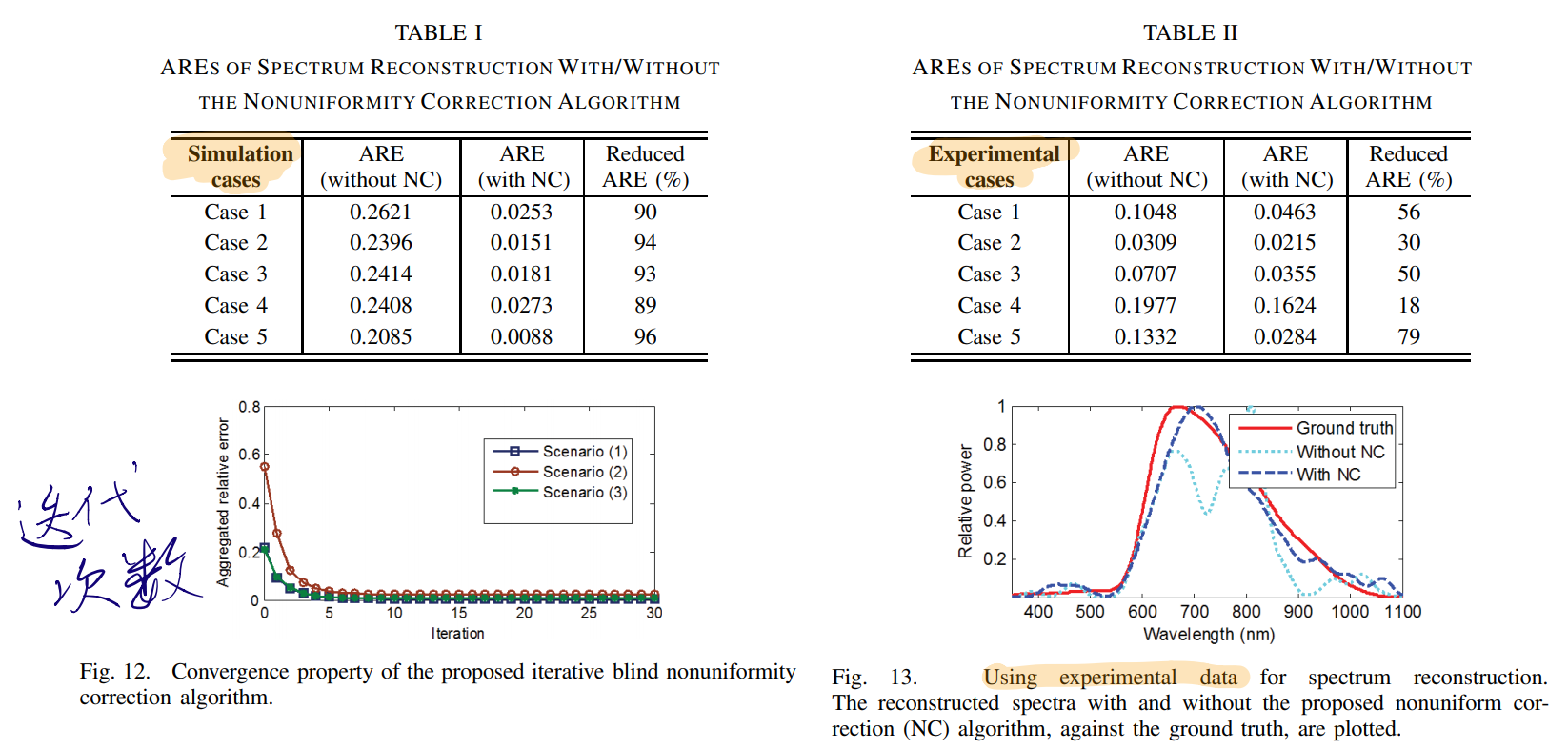
可以看出,由于实际情况各种难以控制的因素影响,算法优化效果要劣于模拟结果,但是仍旧有很大的优化效果。
Paper 4
Title
《基于液晶设备的压缩感知光谱测量方法》
August Y , Stern A . Compressive sensing spectrometry based on liquid crystal devices[J]. Optics Letters, 2013, 38(23):4996-4999.
Contents
本文介绍了一种脱离于香农-奈奎斯特采样定理的新型稀疏采样方法——压缩感知,在目标频谱图稀疏的情况下,通过小规模的随机亚采样(而不是等间隔采样)方式,能够实现对原谱图的重建,该采样方式的理论可行性已经被证明。
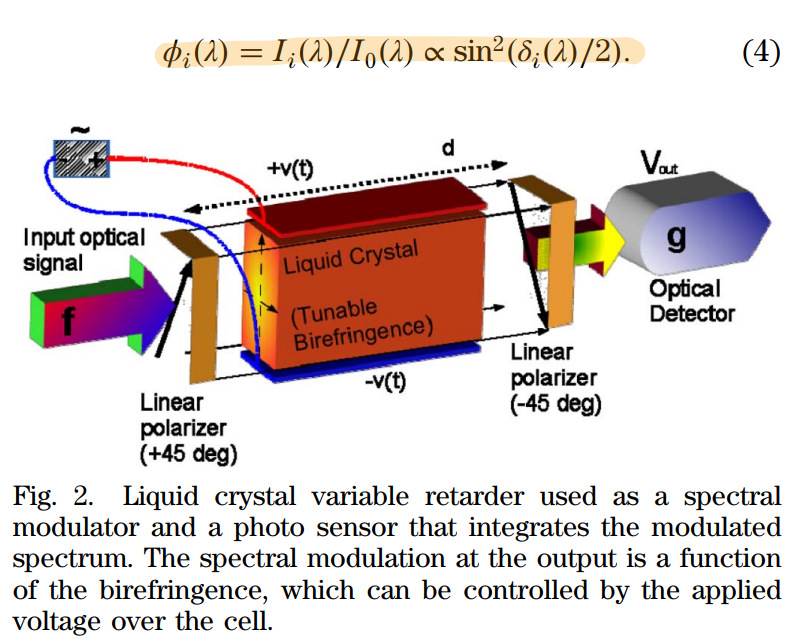
下图是该实验装置图,作者采用各向异性的液晶作为色散元件,通过施加不同大小的电压幅值,使液晶方向发生改变,从而对光线产生不同程度的色散效果,进而可以建立线性方程组求解,可以看到在入射和出射处都加了线性偏振片,以保证光线的偏振效果相同。
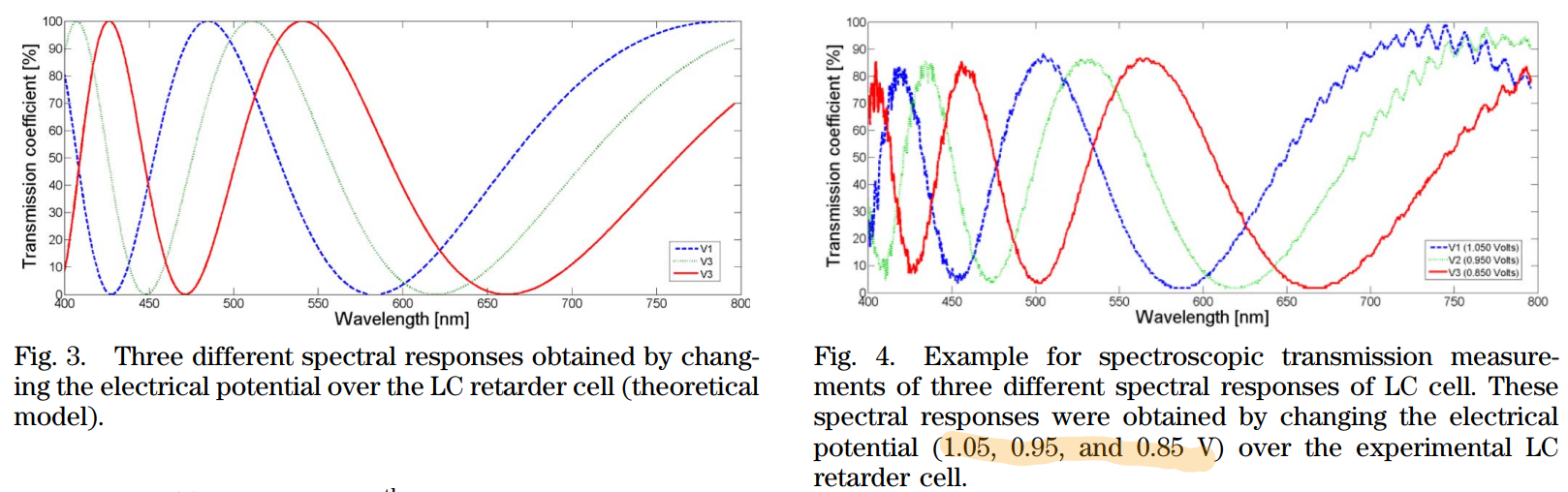
下方,左图为三种理论的液晶对应的光谱传递矩阵,右图为实验测得的结果
Results
最终,传递矩阵可以写为如下形式,作者采用了一些数学方法,将该矩阵等效为了部分的傅里叶矩阵$\phi_i = \frac{1}{2} - \frac{1}{2}\cos(\beta_i\omega)$
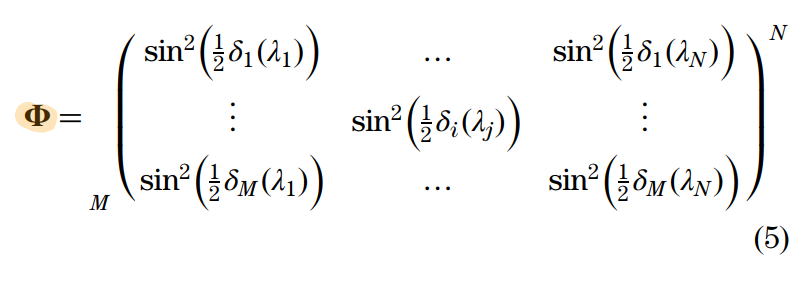
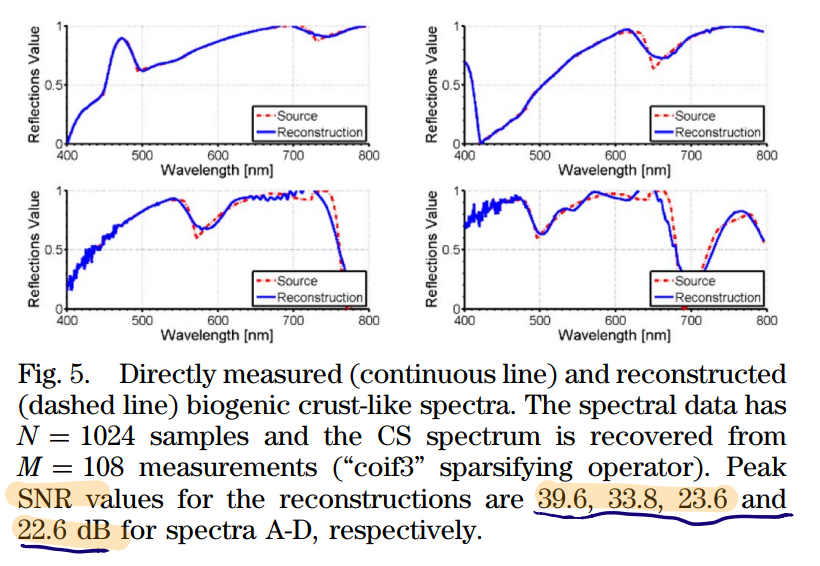
最后,利用TwIST算法解最小二乘,以及Coiflets 3 小波变换实现稀疏采样,实现了重建工作
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!