周报：2020-11-16~2020-11-22

---

Paper 1

Titile

《多模光纤光谱仪，实现高分辨率+低损耗》

[1]Redding Brandon,Cao Hui. Using a multimode fiber as a high-resolution, low-loss spectrometer.[J]. Optics letters,2012,37(16).

Contents

光线在光纤中传播，出口端光场分布（忽略磁场，主要是电场）方程为：

$$E(r,\theta,\lambda,L) = \sum_mA_m\Psi_m(r,\theta,\lambda)\exp[-i(\beta_m(\lambda)L-\omega t)]$$

光纤内部结构通常为 “纤芯+包膜” 形式，不同的导模会导致光线产生不同程度的反射、折射，同时，多模光纤就能够实现对不同波长光的不同导出模式，对应的光纤末端显现的光斑样貌也不同，通过铟镓砷相机捕获光斑，入射光的不同波长光在导模作用下产生不同光斑，依此构建映射关系，得出线性数学模型。

该文献定义了一个correlation function，只有当两个相邻波长光产生 基本上不同 的相关函数值时，才能认定该分辨率可行。

需要了解的是，越长的光纤，能够对入射光传递的变化也越大，即末端收到的信号差别也就越大，因此本论文使用了1m、2m、5m三种长度的光纤作对比。

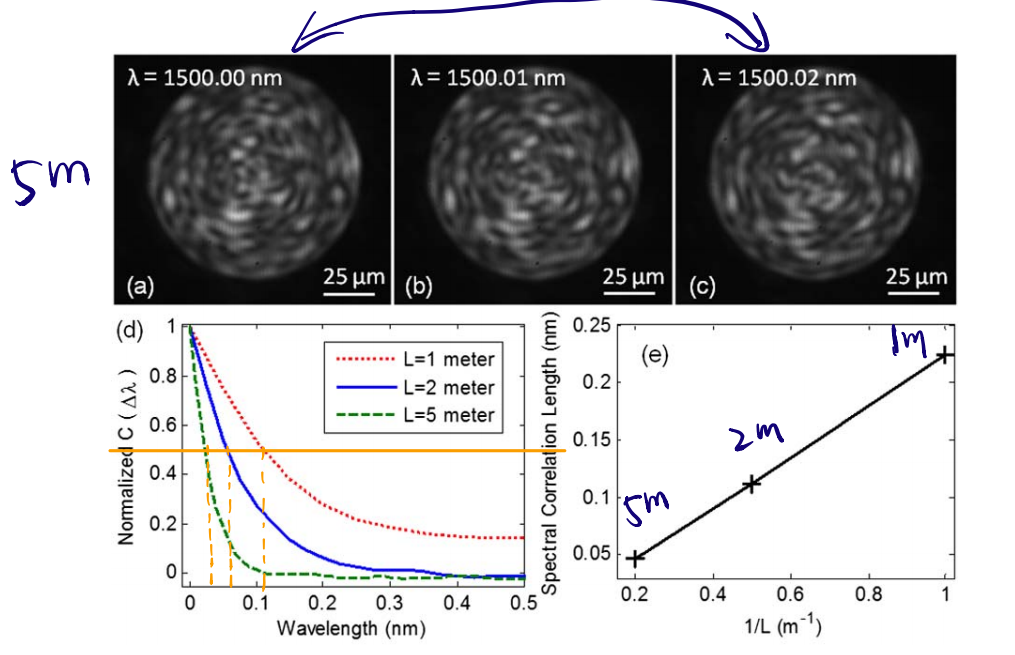
从空间和波长两个方面出发来离散化模型，得到的光斑和传递举证如下图所示

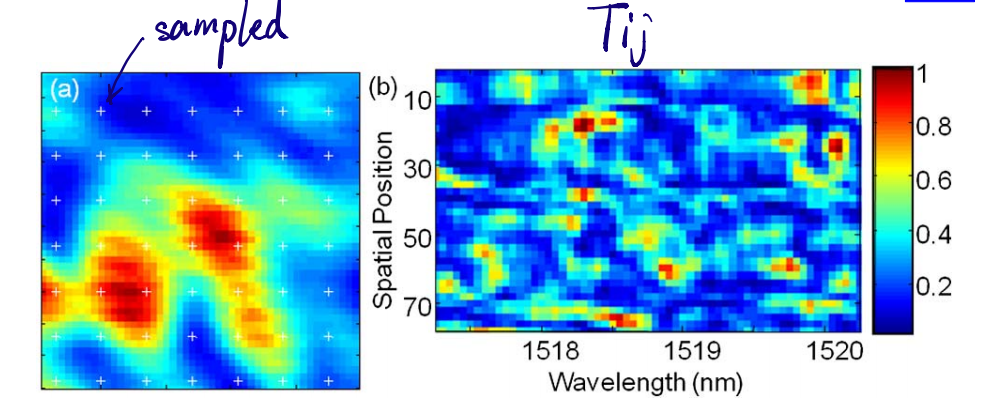
Results

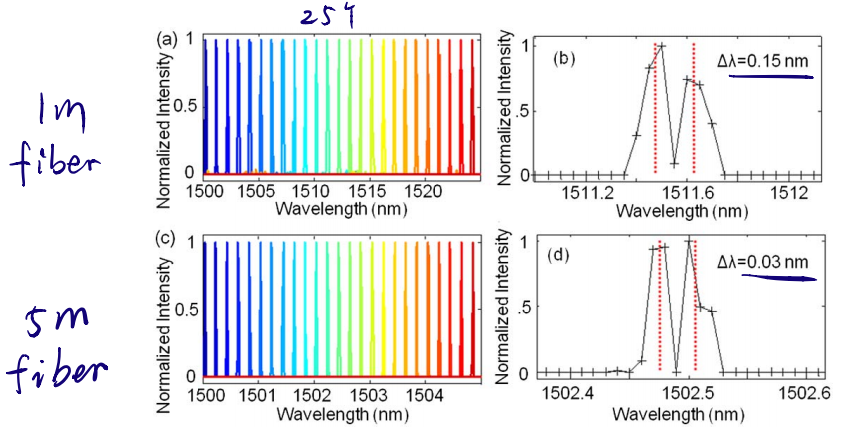
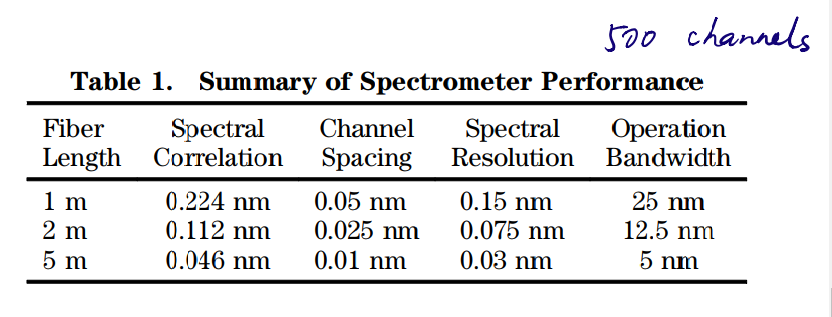
Paper 2

Title

《高分辨率宽谱全光纤光谱仪》

Redding B , Alam M , Seifert M , et al. High-resolution and broadband all-fiber spectrometers[J]. Optica, 2014, 1(3).

Content

承接着上一篇文献，这篇把光纤长度扩展到了100m实现了1pm的分辨率，同时，把长度缩短到了4cm，实现了400~750nm的宽光谱重建。

实验装置是 单模（用于实现同一方向偏振的光） 接 多模（用于实现色散效果）

同样，定义了一个相关函数，并且确定了分辨率为1.5pm

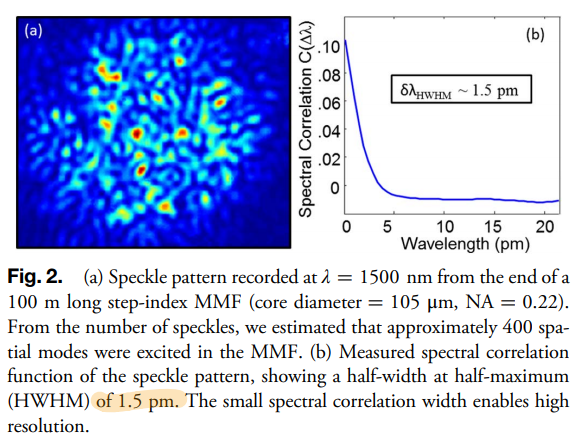
Problem

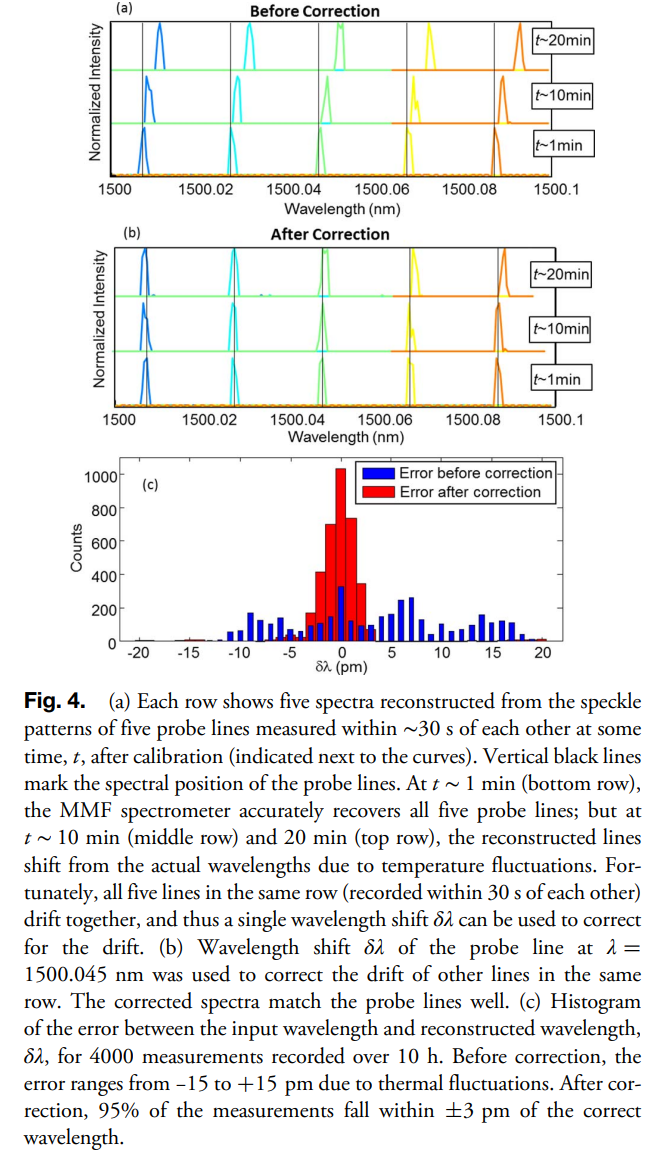
对于长光纤，有一个非常重要的问题，就是它受温度的影响很大，因为它太灵敏了，对于这个问题，作者提出了一个非常简单的数学方法：考虑温度$\delta T$的影响，对于光场函数$E(r,\theta,\lambda,L) = \sum_mA_m\Psi_m(r,\theta,\lambda)\exp[-i(\beta_m(\lambda)L-\omega t)]$的影响最大的一部分就是指数$\beta_mL$这一部分，因为这一部分乘了长度。

作者将同一波长下的温度变化引起的参数变化等效为不同波长下同意温度的参数值，即$\beta_m(\lambda+\delta\lambda,T)L(T) = \beta_m(\lambda,T+\delta T)L(T+\delta T)$，理论上来说，每个导模的波长变化都不同，但是，根据实验结果来看，小范围的温度波动对所有导模波长的影响都是相同的，因此上式成立。

从而可以选取一段波长的参数作为“基底”，实现简单的数学修正

Results