周报：2020-11-2 ~ 2020-11-8

---

Paper1

Title

《基于滤光片光谱仪的目标光谱估计》

[1] Chang Cheng-Chun,Lee Heung-No. On the estimation of target spectrum for filter-array based spectrometers.[J]. Optics express,2008,16(2).

Contents

采用性能较差但成本较低的滤光片（宽谱），利用NNLS（非负最小二乘）算法实现了光谱重建工作

Models

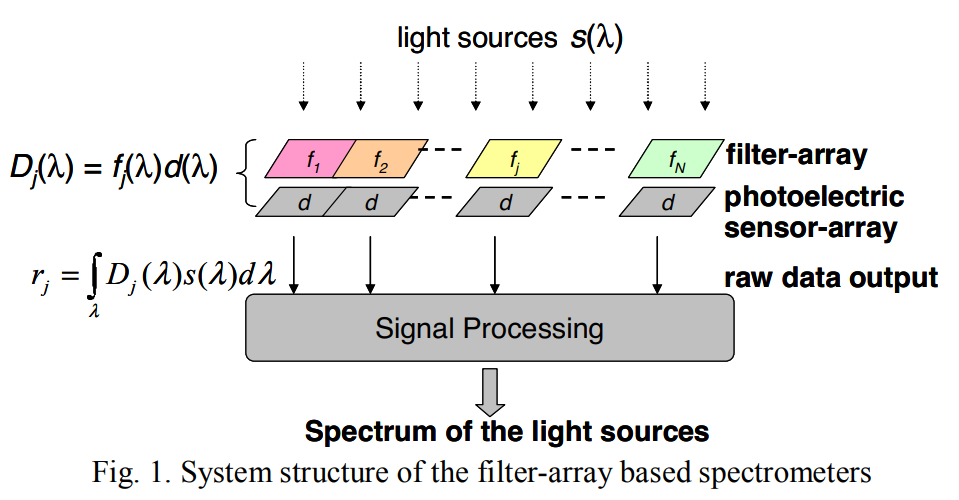
基本数学模型如下图所示：其中向量$r$为观测光谱，$s$为光源原本的光谱值

Solutions

把$s$看作模型参数，$r$是我们已经可以观测到的事件，目的就是需要估计这个模型参数值，也就是一个似然的过程，可以考虑最大后验概率估计MAP，但由于我们没有对模型参数$s$的先验知识，所以这个估计退化为极大似然估计MLE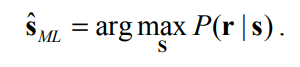

把$r$式代入，显然这个问题取决于噪声的分布情况，考虑将噪声设置为多元高斯分布，那么这个似然函数就变为了高斯函数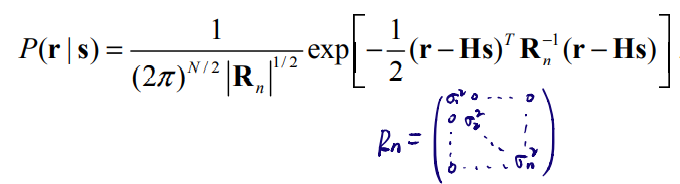

显然，这个函数取得最大值，等价于指数部分取得最小值，经过对指数部分的求导化简，得到解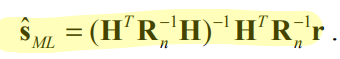：，考虑将噪声函数设置为标准高斯分布，以及H矩阵设置为方正，就可以将解进一步化简为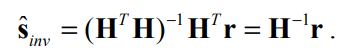

同时，文献说明了在噪声高斯分布的均值为0的情况下，这些估计都是对于光源光谱的无偏估计

这里需要注意的点是：滤光片数量N和取样的波长数量M的关系，由于需要求解$(H^TH)^{-1}$，因此这个$M*M$的矩阵需要满秩，因此必须有$N\ge M$（否则这个矩阵的秩就是N了，不可能满秩了），也就是说滤光片数量需要足够多。同时，文献也简单证明了使用广义逆的有偏问题。

最后，文献介绍了两个算法：SVD（奇异值分解）和NNLS（非负最小二乘），前者就是利用SVD将H矩阵特征提取出来，设置一个Threshold来确定$s$；后者归结为求解下式，采用不断迭代的方法，最终总是可以收敛的。

Experiments

实验设备如下：数字相机（获取光源数据）+计算机（实现算法，绘出图像）+DSP板（数字信号处理）

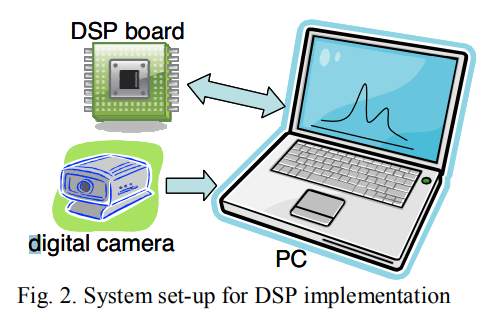
Results

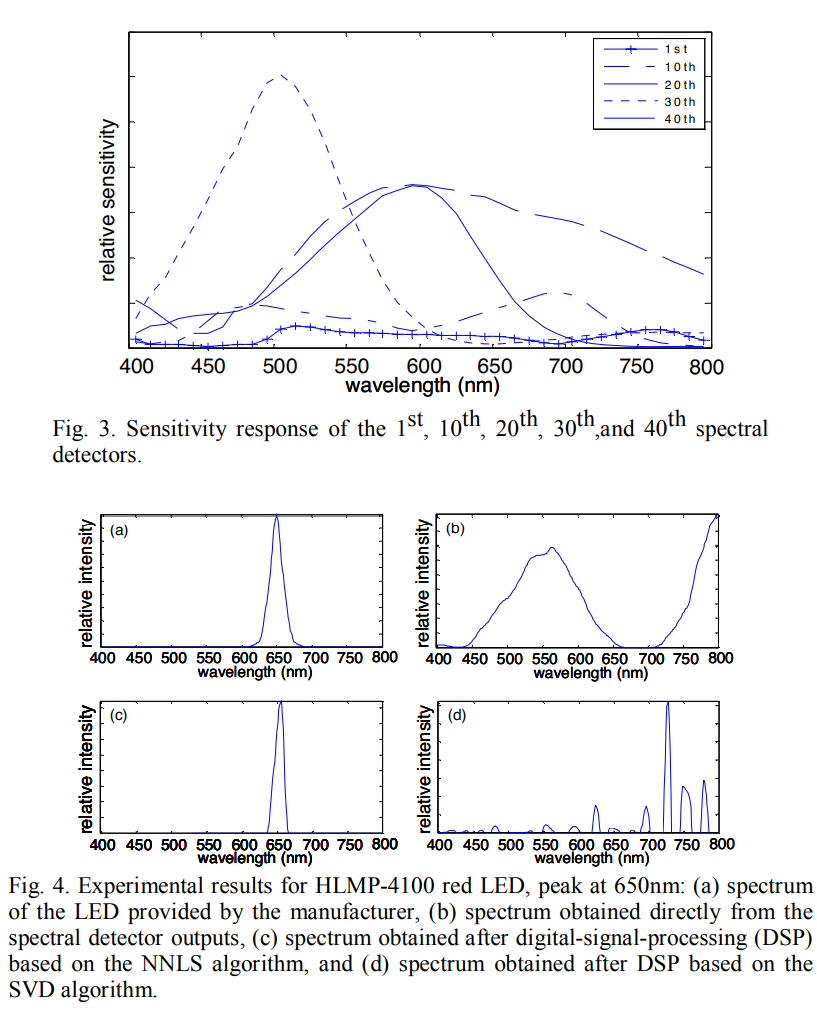
Fig. 3为采用的宽谱滤光片情况，Fig. 4为实验结果，可以看出，NNLS能够很好地还原$s$，而SVD表现很差