周报: 2020.10.19 ~ 2020.10.25

由于很快要踏入研究生生活，为了提前适应每周需要开组会讨论的科研生活，在此blog搭建本人的周报、月报栏目，记录每日所做，每周周日上传周报，月底上传月报，本篇为第一篇，囍。

2020.10.25 周日

由于今天是周日，就不分开写每天做了啥，简单总结一下这一周的工作

实现了LBM简单案例——顶盖驱动流

参考blog：

matlab的模拟结果如下图所示（当然它其实是个动图）：

image-20201025154440608

需要注意的是，matlab代码使用的边界条件为 非平衡态反弹格式（下面是我的笔记，从何雅玲院士书中提炼出的）：

image-20201025155127434

然而这种边界处理对于高雷诺数情况下容易出现发散，对于本案例来说不是很友好，本人尝试将其改为了更为熟练的python代码，如下：

code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl

Lx = 100
Ly = 100

dL = 1
dT = 1

NX = Lx // dL
NY = Ly // dL

w = [4/9, 1/9, 1/9, 1/9, 1/9, 1/36, 1/36, 1/36, 1/36]
e = [[0,0], [1,0], [0,1], [-1,0], [0,-1], [1,1], [-1,1], [-1,-1], [1,-1]]

X = np.arange(NX+1)
Y = np.arange(NY+1)
x,y = np.meshgrid(X,Y)

# plt.plot(x,y)
# plt.show()

rho = np.zeros((NX+1,NY+1))
u = np.zeros((NX+1,NY+1,2))
f = np.zeros((NX+1,NY+1,9))
f_eq = np.zeros((NX+1,NY+1,9))

c = dL / dT 
c_s = c / 3**0.5
rho_0 = 1 # density_0
U = 0.1 # blank speed
Re = 1000
nu = U * Lx / Re
tau = nu / c_s**2 + 0.5 * dT # relaxation time

rho[:,:] = rho_0
u[0,:,0] = U

for i in range(9):
    f[:,:,i] = w[i] * rho[:,:] * (1 + (u[:,:,0]*e[i][0] + u[:,:,1]*e[i][1])/c_s**2 +(u[:,:,0]*e[i][0] + u[:,:,1]*e[i][1])**2/(2*c_s**4) - (u[:,:,0]*u[:,:,0] + u[:,:,1]*u[:,:,1])/(2*c_s**2))

# lbm
MaxIteration = 100
for ite in range(MaxIteration):
    # collision
    for k in range(9):
        f_eq = w[k] * rho[:,:] * (1 + (u[:,:,0]*e[k][0] + u[:,:,1]*e[k][1])/c_s**2 +(u[:,:,0]*e[k][0] + u[:,:,1]*e[k][1])**2/(2*c_s**4) - (u[:,:,0]*u[:,:,0] + u[:,:,1]*u[:,:,1])/(2*c_s**2))
        f[:,:,k] += (f_eq - f[:,:,k]) * dT/tau
    # print('iteration:%d\n'%(ite+1),f,end='\n------------\n')
    # streaming
    f[:,1:,1] = f[:,:NY,1] # left -> right
    f[:,:NY,3] = f[:,1:,3] # right -> left
    f[:NX,:,2] = f[1:,:,2] # bottom -> top
    f[1:,:,4] = f[:NX,:,4] # top -> bottom
    f[:NX,1:,5] = f[1:,:NY,5] # leftbottom -> righttop
    f[1:,:NY,7] = f[:NX,1:,7] # righttop -> leftbottom
    f[1:,1:,8] = f[:NX,:NY,8] # lefttop -> rightbottom
    f[:NX,:NY,6] = f[1:,1:,6] # rightbottom -> lefttop

    # boundary condition
    # left bounce back
    f[:,0,1] = f[:,0,3]
    f[:,0,5] = f[:,0,7]
    f[:,0,8] = f[:,0,6]

    # right bounce back
    f[:,NY,3] = f[:,NY,1]
    f[:,NY,6] = f[:,NY,8]
    f[:,NY,7] = f[:,NY,5]

    # bottom bounce back
    f[NX,:,2] = f[NX,:,4]
    f[NX,:,5] = f[NX,:,7]
    f[NX,:,6] = f[NX,:,8]

    # moving lid
    rho_temp = f[0,1:NY,0]+f[0,1:NY,1]+f[0,1:NY,3]+2*(f[0,1:NY,2]+f[0,1:NY,5]+f[0,1:NY,6])
    f[0,1:NY,4] = f[0,1:NY,2]
    f[0,1:NY,7] = 0.5*f[0,1:NY,1]-0.5*f[0,1:NY,3]+f[0,1:NY,5]-0.5*rho_temp*U
    f[0,1:NY,8] = 0.5*f[0,1:NY,3]-0.5*f[0,1:NY,1]+f[0,1:NY,6]+0.5*rho_temp*U

    rho = np.sum(f,axis=2)

    u = np.zeros((NX+1,NY+1,2))
    for k in range(9):
        u[:,:,0] += f[:,:,k]*e[k][0]
        u[:,:,1] += f[:,:,k]*e[k][1]

    u[:,:,0] /= rho
    u[:,:,1] /= rho

    u[0,1:NY,0] = U
    u[0,1:NY,1] = 0

u_norm = (u[:,:,0]**2 + u[:,:,1]**2)**0.5
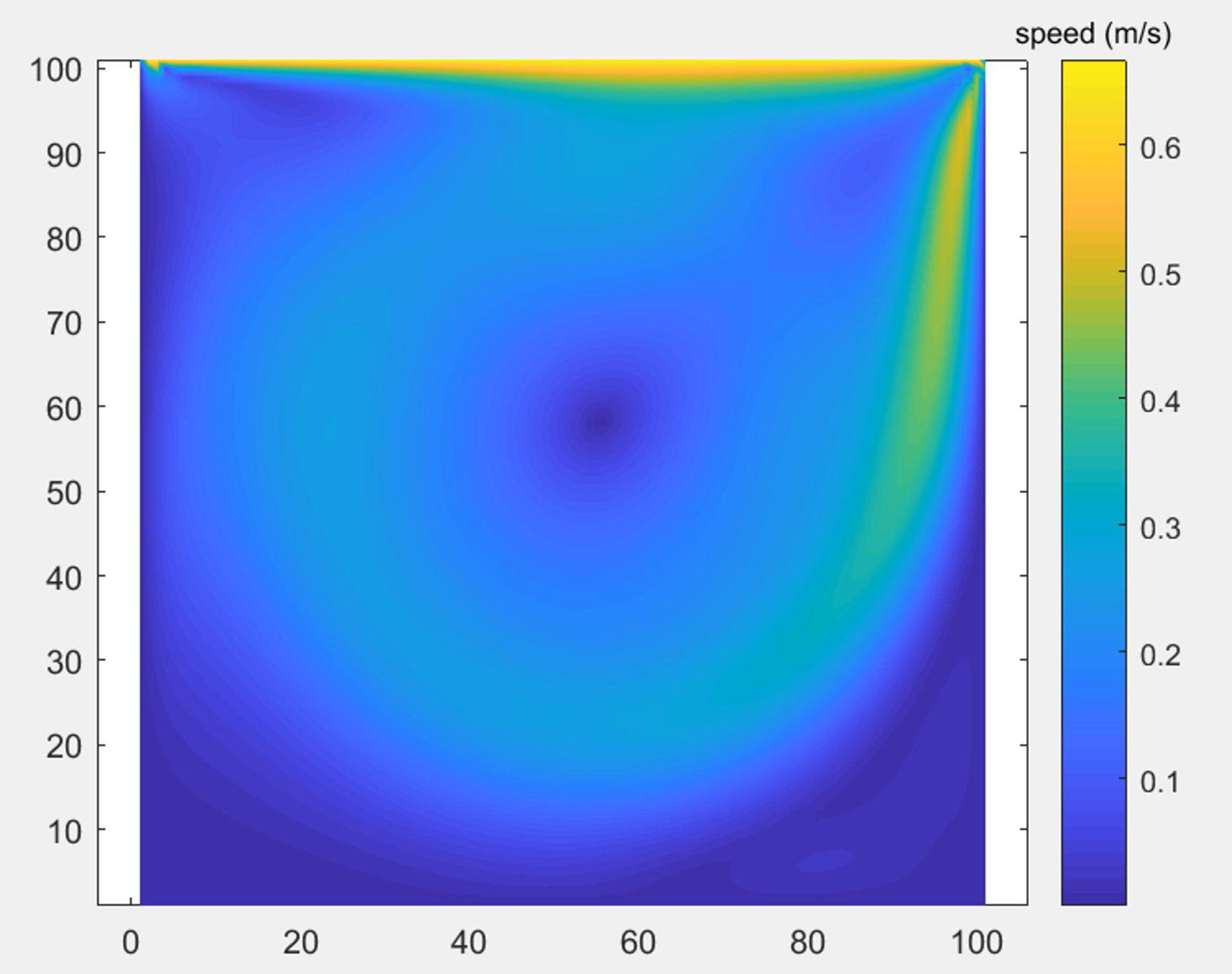
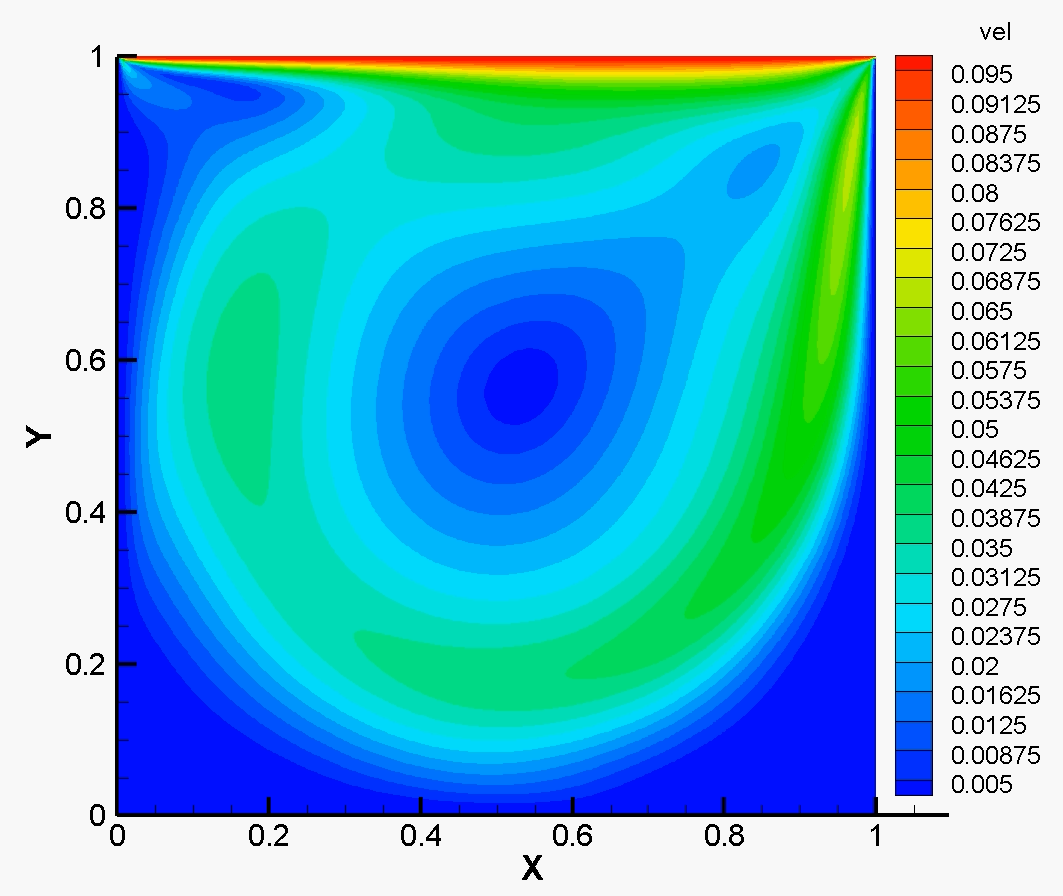
plt.imshow(u_norm)
plt.colorbar()
plt.show()

仍旧会出现发散情况，于是继续查阅资料，在何雅玲院士的书中发现了对于速度边界更为好用的非平衡态外推格式：（附上书上原文和我的简单笔记）

非平衡态外推格式

image-20201025155752200

简单来说就是：对于边界上的节点，若宏观参数未知（比如：密度$\rho$），则用相邻节点的已知参数代替，并用相邻节点的非平衡态函数代替此节点的非平衡态函数，然后加上碰撞项，即可得到此节点的分布函数，最终公式为：（其中O为边界节点，B为其相邻节点）

考虑用C++重构代码，并用tecplot绘制流场图，发现可以任意调整Re数都不会出现发散的情况，其中Re=1000的情况如下图所示：

image-20201025160511465

何院士的代码：

code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
#include<iostream>
#include<cmath>
#include<cstdlib>
#include<iomanip>
#include<fstream>
#include<sstream>
#include<string>
using namespace std;
const int Q=9;
const int NX=256;
const int NY=256;
const double U=0.1;
int e[Q][2]={{0,0},{1,0},{0,1},{-1,0},{0,-1},{1,1},{-1,1},{-1,-1},{1,-1}};
double w[Q]={4.0/9,1.0/9,1.0/9,1.0/9,1.0/9,1.0/36,1.0/36,1.0/36,1.0/36};
double rho[NX+1][NY+1],u[NX+1][NY+1][2],u0[NX+1][NY+1][2],f[NX+1][NY+1][Q],F[NX+1][NY+1][Q];
int i,j,k,ip,jp,n;
double c,Re,dx,dy,Lx,Ly,dt,rho0,P0,tau_f,niu,error;
void init();
double feq(int k,double rho,double u[2]);
void evolution();
void output(int m);
void Error();
int main(){
    using namespace std;
    init();
    for(n=0;;n++){
        evolution();
        if(n%100==0){
            Error();
            cout<<"The"<<n<<"th computation result:"<<endl<<"The u,v of point (NX/2,NY/2)is : "<<setprecision(6)<<u[NX/2][NY/2][0]<<","<<u[NX/2][NY/2][1]<<endl;
            cout<<"The max relative error of uv is:"<<setiosflags(ios::scientific)<<error<<endl;
            if(n>=1000){
                if(n%1000==0) output(n);
                if(error<1.0e-6) break;
            }
        }
    }
    return 0;
}

void init(){
    dx=1.0;
    dy=1.0;
    Lx=dx*double(NY);
    Ly=dy*double(NX);
    dt=dx;
    c=dx/dt;
    rho0=1.0;
    Re=1000;
    niu=U*Lx/Re;
    tau_f=3.0*niu+0.5;
    std::cout<<"tau_f= "<<tau_f<<endl;
    for(i=0;i<=NX;i++)
        for(j=0;j<=NY;j++){
            u[i][j][0]=0;
            u[i][j][1]=0;
            rho[i][j]=rho0;
            u[i][NY][0]=U;
            for(k=0;k<Q;k++){
                f[i][j][k]=feq(k,rho[i][j],u[i][j]);
            }
        }
}

double feq(int k,double rho,double u[2]){
    double eu,uv,feq;
    eu=(e[k][0]*u[0]+e[k][1]*u[1]);
    uv=(u[0]*u[0]+u[1]*u[1]);
    feq=w[k]*rho*(1.0+3.0*eu+4.5*eu*eu-1.5*uv);
    return feq;
}

void evolution()
{
    // collision
    for(i=1;i<NX;i++)
        for(j=1;j<NY;j++)
            for(k=0;k<Q;k++){
                ip=i-e[k][0];
                jp=j-e[k][1];
                F[i][j][k]=f[ip][jp][k]+(feq(k,rho[ip][jp],
                u[ip][jp])-f[ip][jp][k])/tau_f;
            }
    
    // streaming
    for(i=1;i<NX;i++)
        for(j=1;j<NY;j++){
            u0[i][j][0]=u[i][j][0];
            u0[i][j][1]=u[i][j][1];
            rho[i][j]=0;
            u[i][j][0]=0;
            u[i][j][1]=0;
            for(k=0;k<Q;k++){
                f[i][j][k]=F[i][j][k];
                rho[i][j]+=f[i][j][k];
                u[i][j][0]+=e[k][0]*f[i][j][k];
                u[i][j][1]+=e[k][1]*f[i][j][k];
            }
            u[i][j][0]/=rho[i][j];
            u[i][j][1]/=rho[i][j];
        }
    // left & right boundary
    for(j=1;j<NY;j++)
        for(k=0;k<Q;k++){
            rho[NX][j]=rho[NX-1][j];
            f[NX][j][k]=feq(k,rho[NX][j],u[NX][j])+(f[NX-1][j][k]-feq(k,rho[NX-1][j],u[NX-1][j]))*(1-1/tau_f);
            rho[0][j]=rho[1][j];
            f[0][j][k]=feq(k,rho[0][j],u[0][j])+(f[1][j][k]-feq(k,rho[1][j],u[1][j]))*(1-1/tau_f);
        }

    // top & bottom boundary
    for(i=0;i<=NX;i++)
        for(k=0;k<Q;k++){
            rho[i][0]=rho[i][1];
            f[i][0][k]=feq(k,rho[i][0],u[i][0])+(f[i][1][k]-feq(k,rho[i][1],u[i][1]))*(1-1/tau_f);
            rho[i][NY]=rho[i][NY-1];
            u[i][NY][0]=U;
            f[i][NY][k]=feq(k,rho[i][NY],u[i][NY])+(f[i][NY-1][k]-feq(k,rho[i][NY-1],u[i][NY-1]))*(1-1/tau_f);
        }
}

void output(int m){
    ostringstream name;
    name<<"cavity_100_"<<m<<".dat";
    ofstream out(name.str().c_str());
    out<<"Title= \"LBM Lid Driven Flow\"\n"<<"VARIABLES=\"X\",\"Y\",\"U\",\"V\"\n"<<"ZONE T=\"BOX\",I="<<NX+1<<",J="<<NY+1<<",F=POINT"<<endl;
    for(j=0;j<=NY;j++)
        for(i=0;i<=NX;i++){
            out<<double(i)/Lx<<" "<<double(j)/Ly<<" "<<u[i][j][0]<<" "<<u[i][j][1]<<endl;
        }
}

void Error(){
    double temp1,temp2;
    temp1=0;
    temp2=0;
    for(i=1;i<NX;i++)
        for(j=1;j<NY;j++){
            temp1 +=((u[i][j][0]-u0[i][j][0])*(u[i][j][0]-u0[i][j][0])+(u[i][j][1]-u0[i][j][1])*(u[i][j][1]-u0[i][j][1]));
            temp2 +=(u[i][j][0]*u[i][j][0]+u[i][j][1]*u[i][j][1]);
        }
    temp1=sqrt(temp1);
    temp2=sqrt(temp2);
    error=temp1/(temp2+1e-30);
}

传统LBM方法对于大雷诺数的发散情况

对于传统的均分网格lbm方法，对于雷诺数稍大一些（>5000）的情况就会发散，十分让人头疼，因此需要考虑找到处理大雷诺数的情况，需要查阅文献找找方法

利用python分割pdf文件

今天给小组成员发了boltzmann方程的推导过程， 让他们熟悉熟悉，总不能啥也不干吧。。。（打算之后每周都发一点东西给他们看看）

为了更加人性化，我用python切割pdf文件，把电子书的一部分做成pdf发给他们，这样压力会小点，具体代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from PyPDF2 import PdfFileReader, PdfFileWriter

def split(path,name_tit):
    pdf = PdfFileReader(path) # 读取pdf文件
    pagestart = 49 - 1 # 起始页
    pageend = 52 - 1 # 结束页
    pdf_writer = PdfFileWriter() # 创建写入对象
    for idx in range(pagestart,pageend+1):
        pdf_writer.addPage(pdf.getPage(idx)) # 获取页面并添入
    output = f'{name_tit} {pagestart-7}~{pageend-7}.pdf' # 命名
    with open(output, 'wb') as output_file: # 保存为pdf文件
        pdf_writer.write(output_file)


if __name__ == '__main__':
    paht = r'C:\Users\wlx\Desktop\专业创新实践\Boltzmann方法的理论及应用--何雅玲版.pdf'
    split(paht,'boltzmann method')

下周计划

  • 重构一遍顶盖驱动流的C++代码，要熟练掌握

  • 找到处理大雷诺数的方法

  • 熟悉周期性边界条件

  • 计算一个类似于下图所示的简单案例

    image-20201025161043611

  • 应用周期性边界条件，计算一个下图所示案例

    image-20201025161226643