[temp]预测情况汇报2

前段时间一直在准备程序设计竞赛，没有好好做过预测这方面的课题，这几天稍微闲下来一点了，于是就来搞一下。

2020.5.12

由于本课题的问题是需要根据过去的时间序列预测未来的时间序列，也就是所谓的$Sequence-to- Vector$ 的实现，这一点我们无法简单地利用RNN或者LSTM神经网络来进行预测，归根结底就是因为这种时间序列预测的特点是无监督学习：数据集只有时间戳和特征，对于未来需要预测的时间点，只有时间序列作为自变量，因此无法将它简单地转换为监督学习数据集从而使用神经网络预测（神经网络大都是监督学习）

那么，我首先想到的就是利用传统的时间序列分解方法来构建这个模型

模型的算法实现

对于一个时间序列$y_t$，我将其分解为以下几个部分：

  1. 季节项$S_t$（呈周期变化的特征）
  2. 趋势项$T_t$
  3. 剩余项$R_t$

那么，对于所有的$t\ge 0$，都有：$y_t=S_t+T_t+R_t$

当然也可以用乘法构建分解：$y_t=S_t\cdot T_t\cdot R_t$，等号两边取对数，就能得到一个加法构建的分解：$\ln y_t=\ln S_t+\ln T_t+\ln R_t$

整体的算法是基于拟合以上各项，然后累加得出最终的预测函数

那么对于趋势预测，我们需要重点考虑 趋势项$T_t$，对于趋势项的模型拟合，最常用的方法无外乎逻辑回归和分段线性拟合，这里我采用分段线性拟合

众所周知，线性函数形如：$y=kx+b$，由于序列不一定是线性的，我们分段处理，假设时间为$t$，在实际环境中，系数$k$和系数$b$不可能是常数，他们都应该与时间项相关，所以我们定义为$k(t)$和$b(t)$，除此之外，时间序列走势也会变，那么就会出现变点(change point)，我们定义为$S$，这一点已经有学者做了很多研究

现在假设已经放置了$S$个变点，并且处于时间戳$s_j$，那么我们就需要在$s_j$上给出增长率的变化，于是我们可以假设一个向量$\delta\in R^S$，其中$\delta_i$表示在时间戳$s_j$上的增长率的变化量，假设初始的增长率为$k$，则在时间戳$t$上的增长率就是：$k+\sum_{j:t>s_j}\delta_j$，为了简化表达，我写成如下函数的形式：

那么在时间戳$t$上的增长率就是$k+a^T\delta$，$k$能够确定了，同理同样可以得出另外一个参数的表达式为$b+a^T\gamma$，至此，基于分段线性函数的模型如下：（其中，$\gamma$为偏置量）

偏置项的求法为：$\gamma=(\gamma_1,\gamma_2,…,\gamma_S)^T,\gamma_j=-s_j\delta_j$

应用模型

由于FaceBook公司开源的fbprophet库带有了时间序列分解的模型，且原理相同，我查看了其源码，其有关线性分段部分的代码如下，符合我们的模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
@staticmethod
    def piecewise_linear(t, deltas, k, m, changepoint_ts):
        """Evaluate the piecewise linear function.
        Parameters
        ----------
        t: np.array of times on which the function is evaluated.
        deltas: np.array of rate changes at each changepoint.
        k: Float initial rate.
        m: Float initial offset.
        changepoint_ts: np.array of changepoint times.
        Returns
        -------
        Vector y(t).
        """
        # Intercept changes
        gammas = -changepoint_ts * deltas
        # Get cumulative slope and intercept at each t
        k_t = k * np.ones_like(t)
        m_t = m * np.ones_like(t)
        for s, t_s in enumerate(changepoint_ts):
            indx = t >= t_s
            k_t[indx] += deltas[s]
            m_t[indx] += gammas[s]
        return k_t * t + m_t

接下来考虑导入数据集来验证这个模型：（选用的还是加州大学欧文分校的数据集）

导入数据并预处理出时间序列和风速数据，选取其中一天（24h）的数据，图线如下：

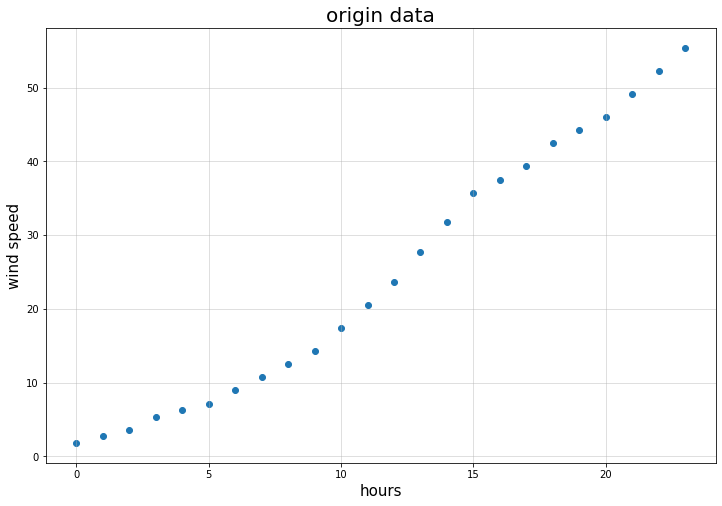
wefwef

对其进行时间序列分解（分段线性拟合），并预测未来一天的数据，得到下图

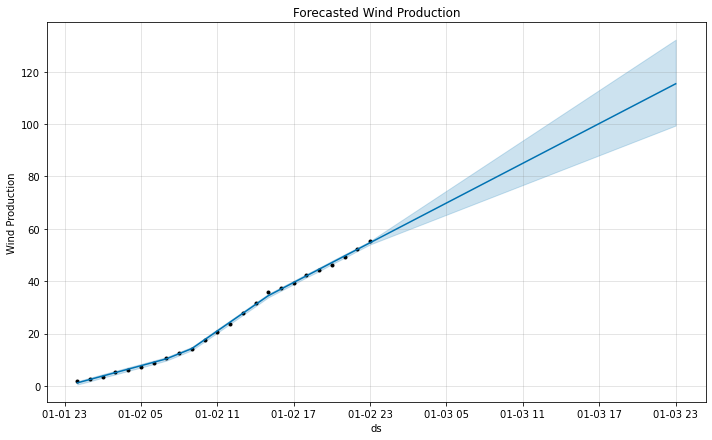
wind2

其中，淡蓝色区域为置信区间，蓝色线为预测线，作出和原始数据的对比图如下：

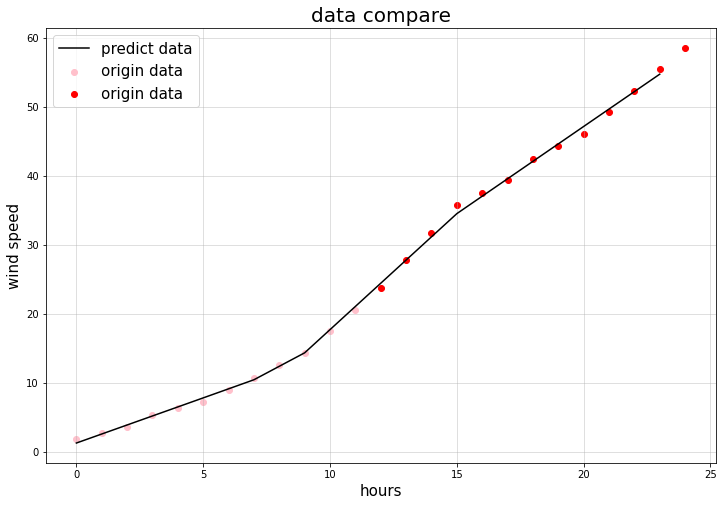
wind3

可以看出效果还是不错的，但这仅限于对于一天内的风速的预测，下面尝试预测一周的时间序列：

找出其中一周的时间序列，原始数据如下图所示

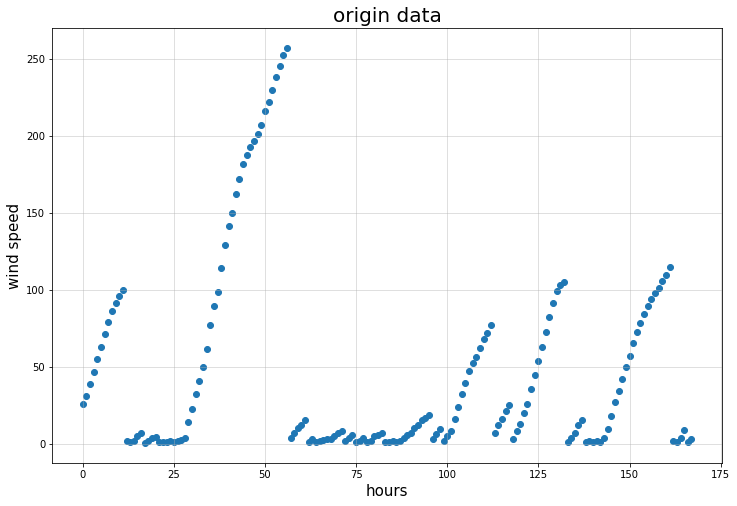
wind4

可以看出每一天风速的数据是十分不稳定的，完全看不出任何规律，因此估计利用分段线性拟合的方法得不出可观的结果，结果如下：

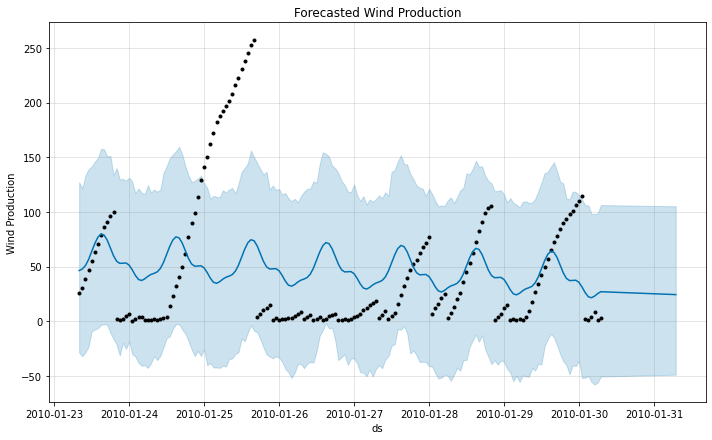
wind51

结果真如所料，得不出可观的结果，究其原因，还是因为风能的日与日之间的数据不具有周期性和规律性的缘故。

2020.5.13

由于之前的预测十分不靠谱，花了一晚上总结了一下，其实数据集也有很大的原因，暂且抛开数据集本身的原因不谈，我先考虑如何使得预测变得稍微靠谱一些。

预测不准的原因显然就是：数据本身没有规律性和周期性，而且数据的波动幅度较大，这一切都是基于每日的小时数据而言的，因此，我可以考虑先放弃处理微观的小时数据，以每日的24小时的数据的均值为研究对象，研究每日风力的均值的变化，那么下面实践一下。

首先仍然是导入数据，然后将每日的24小时风力数据的均值作为研究对象

1
2
3
4
5
y = scaled_data2['y']
y.index=pd.DatetimeIndex(y.index)
daily_wind = y.resample('24H').mean()#24小时的均值为一个数据点
daily_wind = pd.DataFrame(daily_wind)
daily_wind.head()

为了模型预测更准确，进行归一化操作

1
2
3
daily_wind['y']=(daily_wind['y']-daily_wind['y'].mean())/(daily_wind['y'].std())#简单的 减均值再除以标准差 归一化
Mean=daily_wind['y'].mean()
Std=daily_wind['y'].std()

然后，我选取前1400天的数据为训练集，其数据可视化如下：（其中出现了负值是因为我进行了归一化）

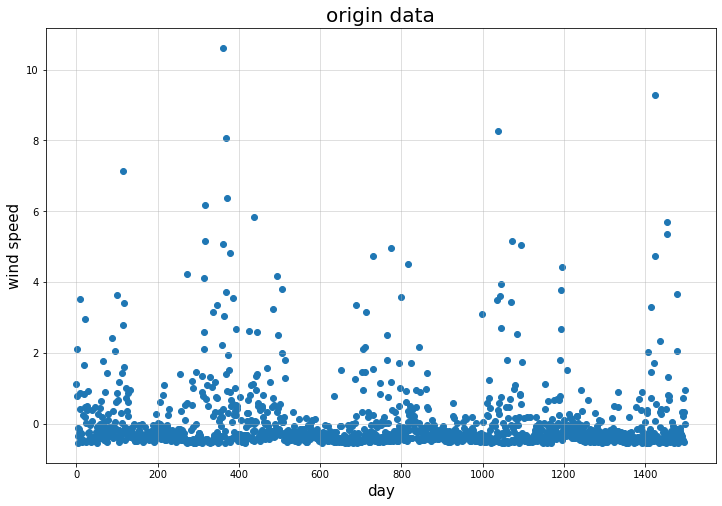
wind21

随后训练模型，并预测后100天的数据，结果如下图所示：

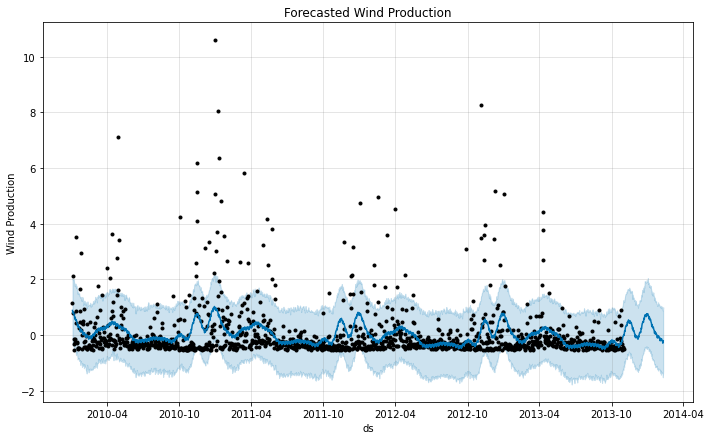
wind22

可以看出，预测线条出现了周期性规律的变化，虽然效果可能不是很好，但已经比昨天的训练好了很多，我们抽出预测的数据和原始数据进行比对，如下图所示：

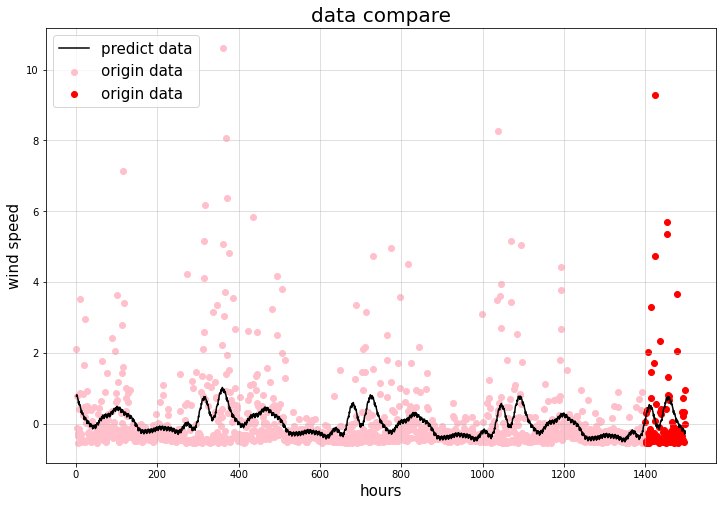
wind23

图中黑色线条为预测线，大红色的散点为原始数据，我们将其放大：

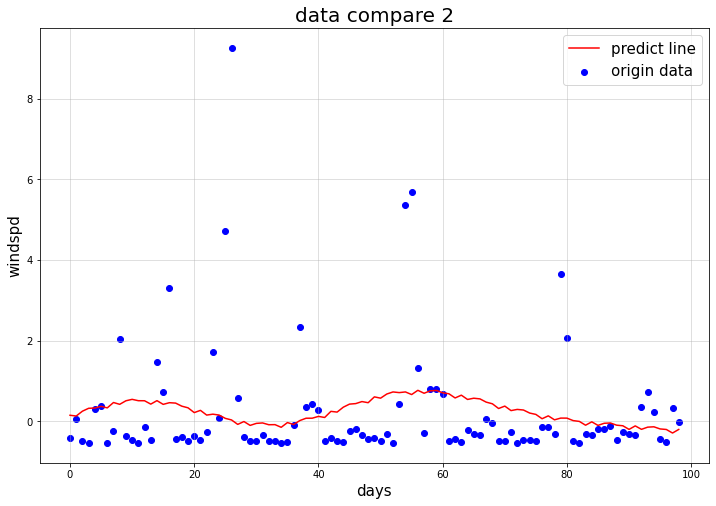
wind24

可以看出，总体的趋势仍然比较平缓，但由于存在一些点的数据值波动十分剧烈，导致这些值完全呈现出不可预测的状态（根本没办法预测出来），这些值的预测线和实际数据偏离很大，很显然这是这个模型的一个无法处理的缺陷

接下来我们定量计算一下实际值和预测值的误差(ERROR)，一般情况下，我们用均方根误差(RMSE)来衡量预测的准确程度，其计算公式如下：

后续 2020.7.1

（前段时间在处理 返校 + 保研夏令营和复习 + 节能减排大赛 的相关事宜，终于忙完，特此记录）

经过一段时间的求证，我发现此类问题与金融大数据科学方面的股票预测十分相似，它们的共同特征都是无规律性，甚至可以说 风能数据比股票数据来得更加无规律无周期。

这一类问题的本质，我的理解是：实现真正意义上的无规律数据+无监督学习预测未来，如果需要对一段无规律数据预测未来的数据值，且需要预测的时间点/段的特征量无输入变量或先验知识，或仅有时间特征作为输入变量，那么这个问题就会变得十分棘手。

但是对应的，我也思考了可能的解决方案，就是：利用容易提前得知或预测到的未来时间点/段 的先验知识/数据 作为输入变量（比如说：我要预测明天中午12点的上海理工大学五食堂门口的风力，那么我可以提前预测明天中午12点的温度、湿度、降雨可能性 等容易提前预测的数据作为未来的先验知识或特征），这样一来，就可以利用$Seq2Seq$模型结合LSTM神经网络或其深度学习模型求解此类问题，结果也许会可观一些。

然而，对于此类问题，我也询问过相关方向（深度学习、预测 相关）的同学和老师，普遍给出的结论就是这类问题难以得出可靠的研究成果，或得出的成果并不具有普适性，因此研究的意义并不是很大，我打算就此告一段落。

虽然并没有得出十分可靠的结论，但此次研究过程中，我阅读了相关文献和博客，学习了许多新的时序建模知识是它带给我的收获。

PS：研究过程中的所有代码和文件见 我的github，这个仓库下的fbprophet和keras内的代码文件就是我的成果。