FFT(快速傅里叶变换)及优化

最近夏令营投递结束了，抽空来学习一波FFT，其中核心内容包括了DFT（离散傅里叶变换）和IDFT（离散傅里叶逆变换），但他们的复杂度都是$O(n^2)$的，我们通过引入单位根及其相关性质将DFT和IDFT优化为FFT和IFFT，实现$O(nlogn)$的复杂度求解多项式卷积系数及相关问题。

参考blog：

• 洛谷P3803 【模板】多项式乘法（FFT） 的所有题解

前置姿势

欧拉公式

$$e^{ix}=\cos{x}+i\cdot \sin{x}$$

单位根

满足$w^n=1$的复数$w$的集合称为$n$次单位根，通常写作$w_n$

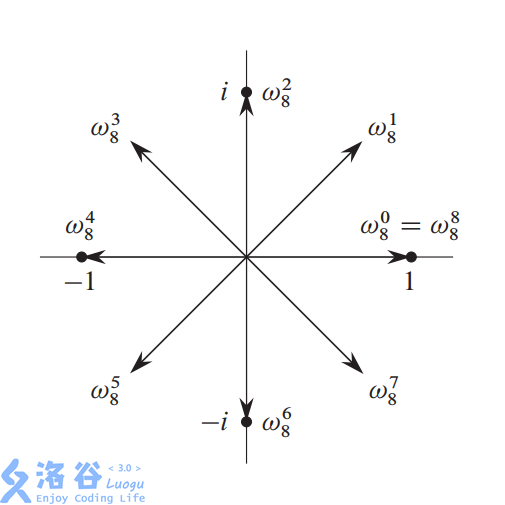
根据欧拉公式，令$x=2\pi$，得到$e^{2\pi i}=1=w_n^n$，得到$w_n=e^{\frac{2\pi i}{n}}$，称为本原单位根，显然

$$w_n=e^{\frac{2\pi i}{n}}=\cos{\frac{2\pi}{n}}+i\cdot \sin{\frac{2\pi}{n}}$$

单位根的一些性质（可以用欧拉公式轻松证得）

• $wn^k=w{2n}^{2k}$

• $w_n^{n+k}=w_n^k$

• $w_n^{k+\frac{n}{2}}=-w_n^k$

• $w_n^{\frac{n}{2}}=-1$

• $w_n^0=w_n^n=1$

多项式的系数表达法

通常情况下，通过多项式方程来表示多项式的方法就是系数表达法，可以直观的看到每项的系数，如$f(x)=3x^3+2x+5$，但如果要通过系数表达法求解两多项式的卷积，显然需要$O(n^2)$的复杂度，不能接受，因此需要考虑换一种方式求解

多项式的点值表达法

众所周知，一个$n$次多项式可以用$n-1$个互不相同的点的坐标来表示，这就是点值表达法，它没有系数表达法那么直观，但显然，如果我们知道两个多项式的系数表达法$(x_0,y0),(x_1,y_1),…$和$(x_0,y_0’),(x_1,y_1’),…$，则可以在$O(n)$的时间内求出$(x_0,y_0y_0’),(x_1,y_1y_1’),…$，即他们卷积的点值表达法

因此，FFT就是通过将多项式的系数表达法转化为点值表达法（DFT），再通过点值表达法求解卷积，再转换回系数表达法（IDFT）的一个计算过程，这个过程乍一看是$o(n^2)$的，因为找出多项式的$n$个点就已经需要$O(n^2)$的时间了（找n个点$O(n)$，计算对应函数值$O(n)$），因此就出现了著名的$FFT$算法

FFT（Fast Fourier Transform）

设$n-1$次多项式$A(x)$的系数为

$$(a_0,a_1,a_2,...,a_{n-1})\\即 A(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1}$$

将下标按照奇偶性分类，得到

$$A(x)=(a_0+a_2x^2+a_4x^4+...+a_{n-2}x^{n-2})\\ +(a_1+a_3x^3+a_5x^5+...+a_{n-1}x^{n-1})$$

设

$$A_1(x)=(a_0+a_2x+a_4x^2+...+a_{n-2}x^{\frac{n}{2}-1})\\ A_2(x)=(a_1+a_3x+a_5x^2+...+a_{n-1}x^{\frac{n}{2}-1})$$

显然可以得到

$$A(x)=A_1(x^2)+xA_2(x^2)$$

此时，将单位根$w_n^k(k<\frac{n}{2})$代入得到

$$\begin{aligned} A(w_n^k)&=A_1(w_n^{2k})+w_n^kA_2(w_n^{2k})\\ &=A_1(w_{\frac{n}{2}}^{k})+w_n^kA_2(w_{\frac{n}{2}}^{k}) \end{aligned}$$

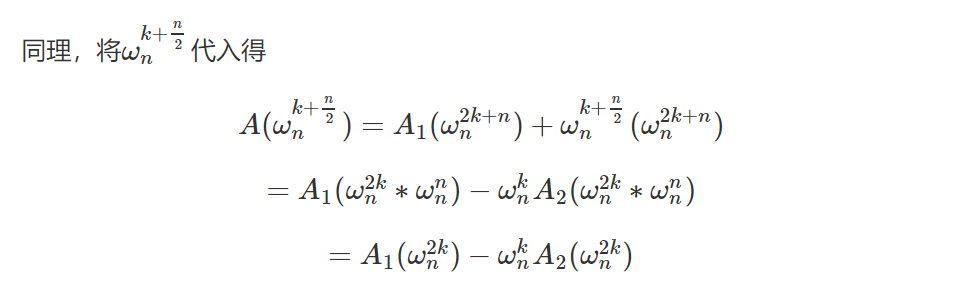
可以惊奇地发现这两个式子就只差了中间一个负号，并且表达式中的$A_1,A_2$规模为$A$的一半，且计算方法相同，因此可以递归分治计算这个式子，递归边界就是仅剩一个项的时候，此时直接返回即可

关于逆变换，先抛出结论：一个多项式在反分治的过程中乘上单位根的共轭复数，分治完的每一项 $/n$即为原多项式的每一项系数

复杂度：$O(nlogn)$，但由于需要递归动态开数组，因此常数较大，但时间复杂度正确

代码（递归版）

int n,m;
complex<double> f[maxn],g[maxn],ans[maxn];

// 递归FFT，type = 1 : DFT ; type = -1 : IDFT
void FFT(complex<double> *a,int n,int type){
	if(n<=1) return;
	int mid=n>>1;
	complex<double> a1[mid],a2[mid];
	for(int i=0;i<mid;i++)
		a1[i]=a[i<<1],a2[i]=a[i<<1|1];
	FFT(a1,mid,type),FFT(a2,mid,type);
	complex<double> w1(cos(PI/mid),type*sin(PI/mid)),w(1,0),x;
	for(int i=0;i<mid;i++){
		x=w*a2[i];
		a[i]=a1[i]+x;
		a[i+mid]=a1[i]-x;
		w*=w1;
	}
}

int main(){
	read(n),read(m);
	for(int i=0,x;i<=n;i++) read(x),f[i]=x;
	for(int i=0,x;i<=m;i++) read(x),g[i]=x;
	int tot=1;
	while(tot<=n+m) tot<<=1;
	FFT(f,tot,1),FFT(g,tot,1);
	rep(i,0,tot) ans[i]=f[i]*g[i];
	FFT(ans,tot,-1);
	rep(i,0,n+m) printf("%d ",(int)(ans[i].real()/tot+0.5));//记得除以tot
	return 0;
}

优化为迭代版本

到洛谷模板一交，由于它时限定在了2s，因此可以通过（最慢的点要1.8s左右），但是我们能够做得更优，为了解决常数较大的问题，我们需要把递归写法改为迭代写法

我们通过将奇偶分治的最终序列手写出来，可以发现一个规律：原序列和分治到最后的序列的对应二进制表示数互为翻转关系，这样一来，从最终分治的结果，我们先计算$a_0/a_2;a_4/a_6;a_1/a_3;a_5/a_7$，然后计算$a_0/a_1;a_2/a_3;a_4/a_5;a_6/a_7$，得到最终结果

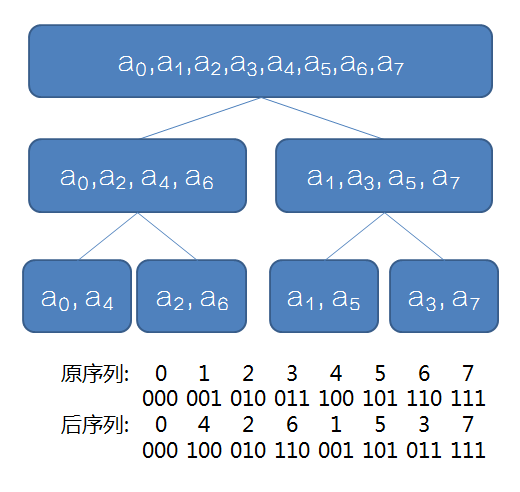
对于二进制翻转的操作，可以使用如下的方法获得，即 得到原序列中的数$i$在翻转序列中的位置$rev[i]$

for(int i=1;i<tot;i++)
		rev[i]=(rev[i>>1]>>1)|((i&1)<<(bi-1));
\*
基本原理：
    原数组的第i位为第i/2位左移得到，则翻转数组就为右移得到
    奇数情况下，原数组+1，翻转数组需要倒着+1
*\

而求出这个$rev[]$数组还不够，我们还需要将原数组重新排列成为翻转序列的顺序，操作如下

for(int i=0;i<n;i++)
		if(i<rev[i]) swap(a[i],a[rev[i]]);

这样一来，我们就可以通过枚举递归分治的区间大小，再枚举区间个数，再枚举区间中每一个数来实现迭代版的FFT

代码（迭代版）

int n,m;
int bi,rev[maxn];
complex<double> f[maxn],g[maxn],ans[maxn];

// 迭代FFT，type = 1 : DFT ; type = -1 : IDFT
void FFT(complex<double> *a,int n,int type){
	for(int i=0;i<n;i++)
		if(i<rev[i]) swap(a[i],a[rev[i]]);
	for(int len=1;len<=(n>>1);len<<=1){
		complex<double> w1(cos(PI/len),type*sin(PI/len));
		for(int i=0;i<=n-(len<<1);i+=len<<1){
			complex<double> w(1,0),x,y;
			for(int j=0;j<len;j++){
				x=a[i+j],y=w*a[i+j+len];
				a[i+j]=x+y,a[i+j+len]=x-y;
				w*=w1;
			}
		}
	}
}

int main(){
	read(n),read(m);
	for(int i=0,x;i<=n;i++) read(x),f[i]=x;
	for(int i=0,x;i<=m;i++) read(x),g[i]=x;
	int tot=1;
	while(tot<=n+m) tot<<=1,bi++;
	for(int i=1;i<tot;i++)
		rev[i]=(rev[i>>1]>>1)|((i&1)<<(bi-1));
	FFT(f,tot,1),FFT(g,tot,1);
	rep(i,0,tot) ans[i]=f[i]*g[i];
	FFT(ans,tot,-1);
	rep(i,0,n+m) printf("%d ",(int)(ans[i].real()/tot+0.5));
	return 0;
}