网络最大流
参考blog:
关于具体的概念知识点,上面两篇博客已经写得十分清楚了,这里主要写一下$Ford-Fulkerson(FF)$算法、$Edmonds-Karp(EK)$算法、$Dinic$算法 这三种算法的代码实现和注意事项以及重难点
LOJ模板题 最大流(需要开long long)
洛谷P3376 【模板】网络最大流(int即可)
FF算法
核心思想:FF算法就是通过DFS的方式不断从源点出发寻找到达汇点的增广路,图中需要取整条路径上的容量的最小值作为这条链(增广路)实际的流量,只要找到了一条到达汇点的增广路,就将这条增广路经过的所有的前向弧减去实际流量值,再将反向弧加上实际流量值,最后返回这条增广路的实际流量即可,如果找不到增广路了,就返回-1(即找不到能加流量了,最大流已经求完)。
时间复杂度上界:$O(mf)$,$f$为最大流,真实情况复杂度 $O(玄学)$
注意事项:
- 每次DFS需要重置标记数组
vis[]=0
- 边从0开始计数,则若正向边为
i,反向边即为i^1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| int n,m,s,t;
bool vis[maxn];
int ff(int u=s,int flow=inf){
if(u==t) return flow;
vis[u]=1;
for(int i=head[u];~i;i=e[i].next){
int v=e[i].v, w=e[i].w, c;
if(!vis[v]&&w>0&&(c=ff(v,min(flow,w)))!=-1){
e[i].w-=c;
e[i^1].w+=c;
return c;
}
}
return -1;
}
inline ll FF(){
ll c,maxflow=0;
while((c=ff())!=-1){
memset(vis,0,sizeof(vis));
maxflow+=(ll)c;
}
return maxflow;
}
|
EK算法
核心思想:EK算法其实就是用BFS实现的FF算法,但通常会比FF算法更优,因为BFS本身就是一个寻找最短路的算法,能够保证每次找到的增广路是最短路,而FF本身是DFS,可能会出现“绕远路”的情况
注意事项:
flow[]数组保存到达每个点的流量值last[]数组保存每次寻找增广路时,到达该点的边的序号,如果为-1则未到达该点- 每次找到增广路后,借助
last[]数组从汇点倒推到源点,过程中执行前向弧减,反向弧加的操作
时间复杂度上界:$O(nm^2)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| int n,m,s,t,flow[maxn],last[maxn];
int ek(){
memset(last,-1,sizeof(last));
queue<int> q;
q.push(s);
flow[s]=inf;
while(!q.empty()){
int u=q.front();
q.pop();
if(u==t) break;
for(int i=head[u];~i;i=e[i].next){
int v=e[i].v,w=e[i].w;
if(w>0&&last[v]==-1){
last[v]=i;
flow[v]=min(flow[u],w);
q.push(v);
}
}
}
return last[t]!=-1;
}
inline ll EK(){
ll maxflow=0;
while(ek()){
maxflow+=(ll)flow[t];
for(int i=t;i!=s;i=e[last[i]^1].v){
e[last[i]].w-=flow[t];
e[last[i]^1].w+=flow[t];
}
}
return maxflow;
}
|
Dinic算法
算法核心:其实是FF和EK算法两者的结合 + 一些骚操作,具体过程是,首先使用BFS对网络图进行分层(其实就是预处理出从源点到达每个其他点的深度,这样可以保证在DFS求增广路时不绕圈、不走回头路),然后通过DFS进行增广,增广过程中只往深度更深的地方增广,此外,还有两个优化过程
- 多路增广:在DFS找到一条增广路后,如果还有剩下的流量,就尝试在该点继续DFS找更多的增广路,即:可以达到一遍DFS找到多条增广路的效果
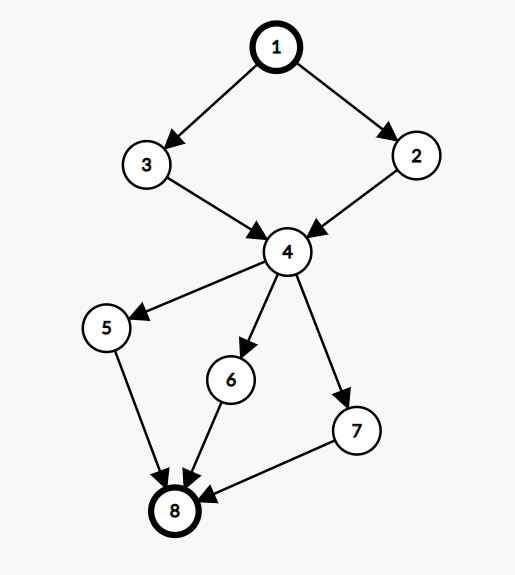
- 当前弧优化(这个我理解了老半天才搞懂它的作用):就是在DFS增广时,对于一个节点,它如果有多条出边,则处理完这些边后,在后续的DFS过程中如果再次经过了这一个节点(如下图中,4点就有可能经过2次)则直接跳过增广过的边(一条边在一次增广过程中只会增广一次),具体实现为:每次增广时,复制一份
head[]数组(命名为cur[]),利用cur[]数组进行图的遍历操作,并不断更新每个点对应的增广的起点
时间复杂度上界:$O(n^2m)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| int n,m,s,t,deep[maxn],cur[maxn];
bool bfs(int s,int t){
for(int i=1;i<=n;i++)
cur[i]=head[i],deep[i]=0;
deep[s]=1;
queue<int> q;
q.push(s);
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u];~i;i=e[i].next){
int v=e[i].v,w=e[i].w;
if(w>0&&!deep[v]){
deep[v]=deep[u]+1;
q.push(v);
}
}
}
return deep[t];
}
int dfs(int u,int t,int flow){
if(u==t) return flow;
int left=flow;
for(int &i=cur[u];~i;i=e[i].next){
int v=e[i].v,w=e[i].w;
if(w>0&&deep[v]==deep[u]+1){
int c=dfs(v,t,min(w,left));
left-=c,e[i].w-=c,e[i^1].w+=c;
if(!left) break;
}
}
return flow-left;
}
inline ll Dinic(){
ll maxflow=0;
while(bfs(s,t)){
maxflow+=(ll)dfs(s,t,inf);
}
return maxflow;
}
|
二分图最大匹配的网络流算法
核心思想:构建出一个虚拟源点和虚拟汇点,从源点向二分图的左部所有点连边,容量为1,从二分图右部所有点向汇点连边,容量为1,对于二分图两部之间的连边,左部连向右部,容量为1,上述连边的同时都需要加一条反向弧,容量为0,最后跑 从源点到汇点的$Dinic$算法即可
证明:略
时间复杂度上界:$O(n\sqrt m)$,优于匈牙利算法的$O(nm)$
模板题代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| inline ll Dinic(){
ll maxflow=0;
while(bfs(1,n+m+2)){
maxflow+=(ll)dfs(1,n+m+2,inf);
}
return maxflow;
}
int main(){
read(n),read(m),read(ee);
init_graph();
for(int i=1,u,v;i<=ee;i++){
read(u),read(v);
addedge(u+1,n+v+1,1),
addedge(n+v+1,u+1,0);
}
for(int i=2;i<=n+1;i++) addedge(1,i,1),addedge(i,1,0);
for(int i=2;i<=m+1;i++) addedge(n+i,n+m+2,1),addedge(n+m+2,n+i,0);
printf("%lld\n",Dinic());
return 0;
}
|
最小费用最大流
