博弈论入门:Nim游戏&SG函数

博弈论のNim游戏&SG函数入门

参考blog：

Nim游戏&博弈游戏基本概念

P2197 【模板】nim游戏

十分经典的博弈游戏，大致规则如下：有两名选手$Alice和Bob$，以及$N$堆石子，第$i$堆中有$A_i$个石子，两个人轮流从任意一堆中取出任意数量的石子（至少取1颗，至多取光这一堆所有石子），当一方无法行动时，另一方获胜，规定$Alice$先手，请你判断在两者足够聪明的情况下，谁会获得胜利？

这是一个典型的ICG游戏（公平组合游戏），对于ICG的定义如下：

  • 两名选手，轮流行动，每次行动可以在有限合法操作集合中选择一个
  • 对于游戏的任何一种可能局面（Position），合法操作集合只取决于这个局面本身，与选手、以前的操作或其他任何因素无关，局面的改变称为“移动”
  • 如果轮到某名移动，且当前局面的合法移动集合为空（无法移动），则该选手判负

对于局面，在博弈论中，有更进一步的定义：

  • P-Position：先手必败 局面
  • N-Position：先手必胜 局面

他们有如下的性质：

  • 合法操作集合为空的局面是P局面
  • 可以移动到P局面的局面是N局面
  • 所有移动都只能到N局面的局面是P局面

对于Nim游戏来说，它有一个神奇的结论：如果$N$堆石子的个数的异或和为$0$（即${xor}_{i=1}^nA_i=0$）则先手必败，否则先手必胜

证明如下：

image.png

简单来说就是：如果当前异或和为0，则下一步操作一定会让异或和变为非零，再下一步操作有至少一种方案能使得异或和为0，如此循环下去，因此如果某一方开局异或和就为0，那么最后某一方的异或和肯定还是为0（即所有石子数量都为0，这是必败的）

SG函数

对于类似于Nim游戏这类ICG来说，都可以通过把局面看成点，每个局面和它的子局面连一条有向边从而抽象成为在一个DAG（有向无环图）上进行的游戏，为了解决通常情况下的ICG游戏问题，便有了定义在DAG上的SG函数

定义

先介绍一下$mex$运算：最小的不属于这个集合的非负整数，例如：$mex{0,1,2,4}=3、mex{2,3,5}=0$

对于一个给定的有向无环图，定义关于图的每个顶点的SG函数如下：

$SG(x)=mex{SG(y)|y是x的后继}$，即 一个点的SG函数为在它所有后继的SG函数未出现过的最小值

性质

  • 对于无后继的点$x$，它的$SG(x)=0$

  • 对于一个$SG(x)=0$的点，如果他有后继，则它的所有后继都满足$SG(y)\neq 0$

  • 对于一个$SG(x)\neq 0$的点，必定存在一个后继$y$满足$SG(y)=0$

发现没有，该性质和ICG游戏的N、P局面是一一对应的，因此，可以理解为：顶点$x$所代表的局面是P局面（先手必败）当且仅当$SG(x)=0$

SG定理

有了这个定理，其实也就就可以解释Nim游戏的P局面为什么是异或和为0先手必败了

模型

例题：取石子问题，有1堆n个的石子，每次只能取${1,3,6}$个石子，先取完石子者胜利，则种局面的SG值为多少？

$x=0,SG(0)=0$

$x=1,可以取走1个石子，SG(1)=mex{SG(1-1)}=mex{SG(0)}=1$

$x=2,可以取走1个石子，SG(2)=mex{SG(2-1)}=mex{SG(1)}=0$

$x=3,可以取走1、3个石子，SG(3)=mex{SG(3-1),SG(3-3)}=mex{SG(2),SG(0)}=1$

$x=4,可以取走1、3个石子，SG(4)=mex{SG(4-1),SG(4-3)}=mex{SG(3),SG(1)}=0$

$x=5,可以取走1、3个石子，SG(5)=mex{SG(5-1),SG(5-3)}=mex{SG(4),SG(2)}=1$

$x=6,可以取走1、3、6个石子，SG(6)=mex{SG(6-1),SG(6-3),SG(6-6)}=mex{SG(5),SG(3),SG(0)}=2$

……

x 0 1 2 3 4 5 6 7 8 …
SG(x) 0 1 0 1 0 1 2 1 2 …

因此，如果有好几堆石子，则根据SG定理，整个游戏的SG函数值就是所有子游戏的SG函数值的异或和，这样便得出了Nim游戏的答案

SG值计算方法

  1. 可选步数为$[1,m]$的连续整数：直接取模即可，$SG(x)=x\ mod\ (m+1)$

  2. 可选步数为任意步：$SG(x)=x$

  3. 可选步数为一系列不连续的数（如例题）：用模板计算

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
inline void get_sg(int n){//一堆有n个石子
    //f是取法集合,功m种取法
    sort(f+1,f+1+m);//坑点，需要先排序，保证每种取法都循环到
    memset(sg,0,sizeof(sg));
    for(int i=1;i<=n;i++){
        memset(vis,0,sizeof(vis));//标记sg函数值有没有出现过
        for(int j=1;f[j]<=i&&j<=m;j++)
            vis[sg[i-f[j]]]=1;//
       	for(int j=0;j<=n;j++)
            if(vis[j]==0){
                sg[i]=j;
                break;
            }
    }
}

阶梯Nim

Nim游戏的变式：有一个$n$层的阶梯，层阶梯上放着不同数量的石子（如图所示），两个人轮流操作，每次可以从任意阶梯取走任意数量的石子放到下一级阶梯中，当一方无法操作时（所有石子都到达地面），另一方获胜

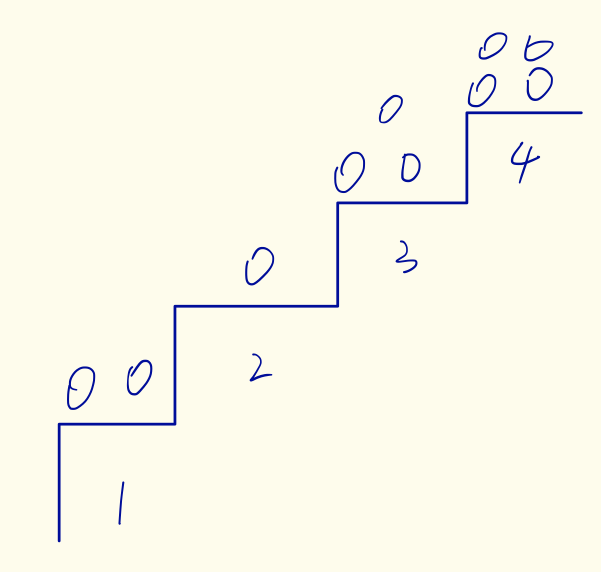
_5D228F52-337F-8BB8-8E41-FC55B110B0DE_.png

这个问题可以将它巧妙地转变成为奇数阶梯层的Nim游戏，为什么呢？

因为：如果对方将一些石子从奇数层放到了下一层（偶数层），那我们就按照Nim游戏一样从奇数层取石子；如果对方将石子从偶数层放到了下一层（奇数层），我们完全可以把对方放置的这一些石子在原封不动地放置到下一层（偶数层），这样一来，奇数层的石子没有发生变化，因此整个问题就转换为了奇数层的Nim游戏，将石子数求异或和判断是否为0即可

练习题：P2575 高手过招（转化阶梯Nim+SG定理）

code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int _,n,pan[21];

int main(){
	for(scanf("%d",&_);_;_--){
		scanf("%d",&n);
		int x,k;
		int ans2=0;
		rep(i,1,n){
			memset(pan,0,sizeof(pan));
			scanf("%d",&x);
			rep(j,1,x){
				scanf("%d",&k);
				pan[k]=1;
			}
			int tp=0,cnt=0,ans1=0;
			int j=20;
			while(pan[j]) j--;
			j--;
			for(;j>=0;j--){
				if(!pan[j]){
					++cnt;
					if(cnt&1) ans1^=tp;
					tp=0;
				}else tp++;
			}
			ans2^=ans1;
		}
		ans2?puts("YES"):puts("NO");
	}
	return 0;
}
算法
博弈论

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！