珂朵莉树ODT 浅析

Chtholly Tree

参考blog：

起源

珂朵莉树（又称Old Driver Tree，简称ODT或老司机树），源自于CF的一道比赛原题：CF896C Willem, Chtholly and Seniorious（因为题目背景是关于珂朵莉的），题意大概就是要求你维护一个神奇数据结构，维护一个具有$n$项的序列，具有如下操作$m$次：

  1. 将$[l,r]$区间所有数加上$x$
  2. 将$[l,r]$区间所有数改成$x$
  3. 输出$[l,r]$区间的第$k$小值
  4. 输出$[l,r]$区间的所有数的$x$次幂之和$(\sum_{i=1}^ra_i^x)\ mod \ y$

数据范围：$1\le n,m \le 10^5$，且保证所有数据随机（即保证1234操作出现的概率相同）

我们可以发现，前两项操作可能用普通线段树就能维护，第三项操作可以用主席树维护，而唯独第四个操作无法在可接受的时间复杂度范围内维护，但是题目说数据随机，因而此刻 珂朵莉树 就华丽登场了~ （面向题目编程）

PS：然而现在的出题人随随便便就能卡掉ODT

实现

珂朵莉树本质上是一种基于$STL$的$std::set$的一种暴力数据机构，适用场合一般具有如下特点：

  • 保证数据随机
  • 需要将一个区间的所有值改为同一个值（推平操作）
  • 含有区间幂次等线段树、BIT无法胜任的操作时

珂朵莉树的每个节点存储的是一段值相同的区间，比如说序列：[1,2,2,2,3,4,4]，在珂朵莉树内的存储方式就是：

L R V
1 1 1
2 4 2
5 5 3
6 7 4

需要注意的是，只有在数据随机的情况下，珂朵莉树中$set$所维护的区间大小才近似于$logn$，整体时间复杂度大致为$O(mlogn)$，然而如果数据不随机，那么这个复杂度就是假的，很可能会退化成暴力($O(m*n)$)的复杂度QWQ

ODT初始化

代码实现如下（珂朵莉树初始化）：

1
2
3
4
5
6
7
8
9
struct odtnode{//ODT树节点
    int l,r;//左右端点
    mutable ll v;//区间值
    odtnode(int L,int R=-1,ll V=0): l(L),r(R),v(V){}
    bool operator <(const odtnode &rhs)const{
        return l<rhs.l;//以左端点升序排序
    }
};
set<odtnode> odt;//set维护的一棵珂朵莉树

接下来就是四个操作的实现了，在这之前，需要介绍一下ODT操作的核心：

$Split$操作

对于一整个区间，每次操作很可能是只需要修改区间的一部分，而另一部分不需要修改，这时，我们可以通过分割操作将区间分割开来，从而只修改需要修改的部分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
set<odtnode>::iterator split(int pos){
    //在pos位置一刀切开，返回右边那个块的迭代器
   	auto it=odt.lower_bound(odtnode(pos));
    //首先找到第一个不小于pos位置的块
    //如果该块的左端点恰好为pos位置，那太好了，直接返回
    if(it!=odt.end()&&it->l==pos)
        return it;
    it--;//否则pos肯定应该位于前一个块中
    int l=it->l,r=it->r;//记录这个块的信息
    ll v=it->v;
    odt.erase(it);//把这块删掉
    odt.insert(odtnode(l,pos-1,v));//沿pos切开后再添加回去
    return odt.insert(odtnode(pos,r,v)).first;
    //最后返回含有pos的右边块的迭代器
}

有了Split操作后，一切都变得好办了

区间推平操作

先将ODT沿区间$[l,r]$切开，然后直接删除中间部分的集合（用$std::set$的$erase$方法，很冷门的方法），再直接插入一整块的相同值的区间集合

这里有个十分难以发现的关键点：一定要先切右端点，再切左端点，否则很可能会玄学RE（在这上面死了好几次）

1
2
3
4
5
6
inline void assign(int l,int r,ll k){
    auto itr=split(r+1),itl=split(l);
    odt.erase(itl,itr);
    //删除区间[itl,itr]中的所有左端点处在这段区间的set元素
    odt.insert(odtnode(l,r,k));//直接插入一整块
}

区间加操作

暴力实现，先沿区间端点切开，然后直接遍历区间内的所有set元素（珂朵莉树节点），将其加上某值（即一整个区间加上某值）

1
2
3
4
inline void add(int l,int r,ll k){
    auto itr=split(r+1),itl=split(l);
    for(;itl!=itr;itl++) itl->v+=k;
}

询问区间第$k$小

暴力实现，先沿区间端点切开，然后直接遍历区间内所有珂朵莉树节点，将其存进一个$vector>$中（其中pair第一个值为权值，第二个值为区间大小，即出现次数），然后对$vector$排序并暴力求$k_{th}$

1
2
3
4
5
6
7
8
9
10
11
12
13
inline ll kth(int l,int r){
    auto itr=split(r+1),itl=split(l);
    vector<pair<ll,int>> vec;
    for(;itl!=itr;itl++){
        vec.push_back(pair<ll,int>(itl->v,itl->r-itl->l+1));
    }
    sort(vec.begin(),vec.end());//按照权值从小到大排序
    for(auto it=vec.begin();it!=vec.end();it++){
        k-=it->second;
        if(k<=0) return it->first;
    }
    return -1ll;//如果没有就返回-1
}

求区间$[l,r]$的$(\sum_{i=l}^ra_i^x)\ mod\ y$

还是暴力实现（结合快速幂），类似于询问询问第$k$小，先切开后，遍历每一个节点，更新答案（加上 区间大小*该区间值的x次幂），累加最后返回即可

1
2
3
4
5
6
7
8
inline ll getxpow(int l,int r,int x,int y){
    auto itr=split(r+1),itl=split(l);
    ll res=0;
    for(;itl!=itr;itl++){
        res=((res+(itl->r-itl->l+1)*qpow(it->v,x,y))%y+y)%y;
    }
    return res;
}

至此，珂朵莉树模板题的完整操作就介绍完毕了，下面奉上完整代码

code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
//略去头文件
//CF896C ODT
ll n,m,vmax,seed;
inline ll rnd(){
	ll ret=seed;
	seed=(seed*7+13)%mod;
	return ret;
}

struct odtnode // ODT Tree
{
	ll l,r;
	mutable ll v;
	odtnode(ll L,ll R=-1,ll V=0):l(L),r(R),v(V){}
	bool operator <(const odtnode &rhs)const{
		return l<rhs.l;
	}
};

set<odtnode> odt;

set<odtnode>::iterator split(ll pos){
	auto it=odt.lower_bound(odtnode(pos));
	if(it!=odt.end()&&it->l==pos) return it;
	it--;
	ll l=it->l,r=it->r,v=it->v;
	odt.erase(it);
	odt.insert(odtnode(l,pos-1,v));
	return odt.insert(odtnode(pos,r,v)).first;
}

inline void add(ll l,ll r,ll k){
	auto itr=split(r+1),itl=split(l);
	for(;itl!=itr;itl++) itl->v+=k;
}

inline void modify(ll l,ll r,ll k){
	auto itr=split(r+1),itl=split(l);
	odt.erase(itl,itr);
	odt.insert(odtnode(l,r,k));
}

inline ll kth(ll l,ll r,ll k){
	auto itr=split(r+1),itl=split(l);
	vector<pair<ll,ll>> vec;
	vec.clear();
	for(;itl!=itr;itl++)
		vec.push_back(pair<ll,ll>(itl->v,itl->r-itl->l+1));
	sort(vec.begin(),vec.end());
	for(vector<pair<ll,ll>>::iterator it=vec.begin();it!=vec.end();it++){
		k-=it->second;
		if(k<=0) return it->first;
	}
	return -1ll;
}

inline ll psum(ll l,ll r,ll x,ll y){
	auto itr=split(r+1),itl=split(l);
	ll res=0;
	for(;itl!=itr;itl++){
		res=(res+(itl->r-itl->l+1)*qpow(itl->v,x,y)%y+y)%y;
	}
	return res%y;
}

int main(){
	scanf("%lld%lld%lld%lld",&n,&m,&seed,&vmax);
	rep(i,1,n) odt.insert(odtnode(i,i,rnd()%vmax+1));
	
	rep(i,1,m){
		ll x,y;
		ll op=(rnd()%4)+1;
		ll l=(rnd()%n)+1;
		ll r=(rnd()%n)+1;
		if(l>r) swap(l,r);
		if(op==3) x=(rnd()%(r-l+1))+1;
		else x=(rnd()%vmax)+1;
		if(op==4) y=(rnd()%vmax)+1;
		if(op==1) add(l,r,x);
		if(op==2) modify(l,r,x);
		if(op==3) printf("%lld\n",kth(l,r,x));
		if(op==4) printf("%lld\n",psum(l,r,x,y));
	}
	return 0;
}

习题

动态开点code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
int n,q,l,r,k;
int mtg[maxn*50],ls[maxn*50],rs[maxn*50],sum[maxn*50],rt,ncnt;

inline void push_up(int o){
	sum[o]=sum[ls[o]]+sum[rs[o]];
}

inline void push_down(int &o,int l,int r){
	if(mtg[o]==-1) return;
	if(!ls[o]) ls[o]=++ncnt;
	if(!rs[o]) rs[o]=++ncnt;
	int mid=(l+r)>>1;
	sum[ls[o]]=mtg[o]*(mid-l+1);
	sum[rs[o]]=mtg[o]*(r-mid);
	mtg[ls[o]]=mtg[rs[o]]=mtg[o];
	mtg[o]=-1;
}

inline void to_(int &o,int l,int r,int L,int R,int k){
	if(!o) o=++ncnt;
	if(l>=L&&r<=R){
		sum[o]=k*(r-l+1);
		mtg[o]=k;
		return;
	}
	push_down(o,l,r);
	int mid=(l+r)>>1;
	if(mid>=L) to_(ls[o],l,mid,L,R,k);
	if(mid+1<=R) to_(rs[o],mid+1,r,L,R,k);
	push_up(o);
}

int main(){
	scanf("%d%d",&n,&q);
	memset(mtg,-1,sizeof(mtg));
	rep(i,1,q){
		scanf("%d%d%d",&l,&r,&k);
		if(k==2) to_(rt,1,n,l,r,0);
		else to_(rt,1,n,l,r,1);
		printf("%d\n",n-sum[rt]);
	}
	return 0;
}
ODT code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
int n,q,l,r,k,sum;

struct odtnode // ODT Tree
{
	ll l,r;
	mutable ll v;
	odtnode(ll L,ll R=-1,ll V=0):l(L),r(R),v(V){}
	bool operator <(const odtnode &rhs)const{
		return l<rhs.l;
	}
};

set<odtnode> odt;

set<odtnode>::iterator split(ll pos){
	auto it=odt.lower_bound(odtnode(pos));
	if(it!=odt.end()&&it->l==pos) return it;
	it--;
	ll l=it->l,r=it->r,v=it->v;
	odt.erase(it);
	odt.insert(odtnode(l,pos-1,v));
	return odt.insert(odtnode(pos,r,v)).first;
}

inline void modify(ll l,ll r,ll k){
	auto itr=split(r+1),itl=split(l);
	auto it=itl;
	for(;it!=itr;it++){
		sum-=it->v*(it->r-it->l+1);
	}
	odt.erase(itl,itr);
	odt.insert(odtnode(l,r,k));
	sum+=k*(r-l+1);
}

int main(){
	scanf("%d%d",&n,&q);
	odt.insert(odtnode{1,n,0});
	sum=0;
	rep(i,1,q){
		scanf("%d%d%d",&l,&r,&k);
		if(k==1) modify(l,r,1);
		else modify(l,r,0);
		printf("%d\n",n-sum);
	}
	return 0;
}

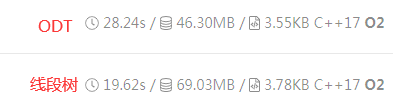
珂朵莉树最慢的点2s，线段树1s，本题时限4s（ODT水过了2333）

image.png

Segment Tree code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
int n,q;

struct Edge{
	int u,v,w,next;
}e[maxn<<1];
int cnt,head[maxn];
inline void init_graph(){
	cnt=0;
	memset(head,-1,sizeof(head));
}
inline void addedge(int u,int v,int w=0){
	e[cnt]=Edge{u,v,w,head[u]};
	head[u]=cnt++;
}

struct Stree
{
	int l,r,sum,tg;
}tr[maxn<<2];

inline void push_down(int i){
	if(tr[i].tg==-1) return;
	int k=tr[i].tg;
	tr[ls].sum=(tr[ls].r-tr[ls].l+1)*k;
	tr[rs].sum=(tr[rs].r-tr[rs].l+1)*k;
	tr[ls].tg=tr[rs].tg=k;
	tr[i].tg=-1;
}
inline void push_up(int i){
	tr[i].sum=tr[ls].sum+tr[rs].sum;
}
inline void add(int i,int l,int r,int k){
	if(tr[i].l>=l&&tr[i].r<=r){
		tr[i].sum=(tr[i].r-tr[i].l+1)*k;
		tr[i].tg=k;
		return;
	}
	push_down(i);
	if(tr[ls].r>=l) add(ls,l,r,k);
	if(tr[rs].l<=r) add(rs,l,r,k);
	push_up(i);
}

inline void build(int i,int l,int r){
	tr[i].l=l,tr[i].r=r,tr[i].tg=-1;
	if(l==r){
		tr[i].sum=0;
		return ;
	}
	int mid=(l+r)>>1;
	build(ls,l,mid);
	build(rs,mid+1,r);
	push_up(i);
}

inline int getval(int i,int pos){
	if(tr[i].l==tr[i].r) return tr[i].sum;
	push_down(i);
	int res=0;
	if(tr[ls].r>=pos) res=getval(ls,pos);
	else res=getval(rs,pos);
	return res;
}

/* Heavy Path Decomposition */
// dfs序、深度、子树大小、父节点、重儿子、链顶
int dfsx,csid[maxn],csdep[maxn],cssize[maxn],csfa[maxn],csson[maxn],cstop[maxn];
// value need to maintain
int csw[maxn];

// first dfs
inline void csdfs1(int u,int fath,int depth){
	csfa[u]=fath;
	csdep[u]=depth;
	cssize[u]=1;
	/* long path dec */
	// cssize[u]=csdep[u];
	for(int i=head[u];~i;i=e[i].next){
		int v=e[i].v;
		if(v!=fath){
			/* edge to point */
			// w[v]=e[i].w;
			// wdep[v]+=w[v];
			csdfs1(v,u,depth+1);
			cssize[u]+=cssize[v];
			/* long path dec */
			// cssize[u]=max(cssize[u],cssize[v]);
			if(cssize[v]>cssize[csson[u]])
				csson[u]=v;
		}
	}
}

//second dfs
inline void csdfs2(int u,int topf){
	csid[u]=++dfsx;
	/* value need to maintain */
	// csw[dfsx]=u;
	cstop[u]=topf;
	if(!csson[u]) return;
	csdfs2(csson[u],topf);
	for(int i=head[u];~i;i=e[i].next){
		int v=e[i].v;
		if(v!=csfa[u]&&v!=csson[u])
			csdfs2(v,v);
	}
}
/*--------------------------------------*/
inline void addrt(int x){
	add(1,csid[x],csid[x]+cssize[x]-1,1);
}

inline void droprt(int x){
	int y=1;
	while(cstop[x]!=cstop[y]){
		if(csdep[cstop[x]]<csdep[cstop[y]])
			swap(x,y);
		add(1,csid[cstop[x]],csid[x],0);
		x=csfa[cstop[x]];
	}
	if(csdep[x]>csdep[y]) swap(x,y);
	add(1,csid[x],csid[y],0);
}

inline int isfull(int x){
	return getval(1,csid[x]);
}

int main(){
	scanf("%d",&n);
	init_graph();
	int x,y;
	rep(i,1,n-1){
		scanf("%d%d",&x,&y);
		addedge(x,y),addedge(y,x);
	}
	csdfs1(1,-1,1);
	csdfs2(1,1);
	build(1,1,n);
	scanf("%d",&q);
	while(q--){
		scanf("%d%d",&x,&y);
		if(x==1) addrt(y);
		if(x==2) droprt(y);
		if(x==3) printf("%d\n",isfull(y));
	}
	return 0;
}
ODT code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
int n,q;

struct Edge{
	int u,v,w,next;
}e[maxn<<1];
int cnt,head[maxn];
inline void init_graph(){
	cnt=0;
	memset(head,-1,sizeof(head));
}
inline void addedge(int u,int v,int w=0){
	e[cnt]=Edge{u,v,w,head[u]};
	head[u]=cnt++;
}

#define IT set<odtnode>::iterator
struct odtnode
{
	int l,r;
	mutable ll v;
	odtnode(int L,int R=-1,ll V=0):l(L),r(R),v(V){}
	bool operator <(const odtnode& rhs)const{
		return l<rhs.l;
	}
};
set<odtnode> odt;

inline IT split(int pos){
	IT it=odt.lower_bound(odtnode(pos));
	if(it!=odt.end()&&it->l==pos) return it;
	it--;
	int l=it->l,r=it->r;
	ll v=it->v;
	odt.erase(it);
	odt.insert(odtnode(l,pos-1,v));
	return odt.insert(odtnode(pos,r,v)).first;
}

// Assign to same value
inline void assign(int l,int r,ll k){
	IT itr=split(r+1),itl=split(l);
	odt.erase(itl,itr);
	odt.insert(odtnode(l,r,k));
}

/*------------------------------------*/
/* Heavy Path Decomposition */
// dfs序、深度、子树大小、父节点、重儿子、链顶
int dfsx,csid[maxn],csdep[maxn],cssize[maxn],csfa[maxn],csson[maxn],cstop[maxn];
// value need to maintain
int csw[maxn];

// first dfs
inline void csdfs1(int u,int fath,int depth){
	csfa[u]=fath;
	csdep[u]=depth;
	cssize[u]=1;
	/* long path dec */
	// cssize[u]=csdep[u];
	for(int i=head[u];~i;i=e[i].next){
		int v=e[i].v;
		if(v!=fath){
			/* edge to point */
			// w[v]=e[i].w;
			// wdep[v]+=w[v];
			csdfs1(v,u,depth+1);
			cssize[u]+=cssize[v];
			/* long path dec */
			// cssize[u]=max(cssize[u],cssize[v]);
			if(cssize[v]>cssize[csson[u]])
				csson[u]=v;
		}
	}
}

//second dfs
inline void csdfs2(int u,int topf){
	csid[u]=++dfsx;
	/* value need to maintain */
	// csw[dfsx]=u;
	cstop[u]=topf;
	if(!csson[u]) return;
	csdfs2(csson[u],topf);
	for(int i=head[u];~i;i=e[i].next){
		int v=e[i].v;
		if(v!=csfa[u]&&v!=csson[u])
			csdfs2(v,v);
	}
}
/*--------------------------------------*/
inline void addrt(int x){
	assign(csid[x],csid[x]+cssize[x]-1,1);
}

inline void droprt(int x){
	int y=1;
	while(cstop[x]!=cstop[y]){
		if(csdep[cstop[x]]<csdep[cstop[y]])
			swap(x,y);
		assign(csid[cstop[x]],csid[x],0);
		x=csfa[cstop[x]];
	}
	if(csdep[x]>csdep[y]) swap(x,y);
	assign(csid[x],csid[y],0);
}

inline int isfull(int x){
	IT it=split(csid[x]);
	return it->v;
}

int main(){
	scanf("%d",&n);
	init_graph();
	int x,y;
	rep(i,1,n-1){
		scanf("%d%d",&x,&y);
		addedge(x,y),addedge(y,x);
	}
	csdfs1(1,-1,1);
	csdfs2(1,1);
	odt.insert(odtnode(1,n,0));
	scanf("%d",&q);
	while(q--){
		scanf("%d%d",&x,&y);
		if(x==1) addrt(y);
		if(x==2) droprt(y);
		if(x==3) printf("%d\n",isfull(y));
	}
	return 0;
}

很遗憾，此题用ODT会T掉最后一个点（因为有人造数据卡ODT），但是可以用来骗分（然而我已经是大学生了），正解是线段树

ODT code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
int n,m,op,l,r;
char x,s[maxn];
#define IT set<odtnode>::iterator
struct odtnode
{
	int l,r;
	mutable int v;
	odtnode(int L,int R=-1,int V=0):l(L),r(R),v(V){}
	bool operator <(const odtnode& rhs)const{
		return l<rhs.l;
	}
};
set<odtnode> odt;

inline IT split(int pos){
	IT it=odt.lower_bound(odtnode(pos));
	if(it!=odt.end()&&it->l==pos) return it;
	it--;
	int l=it->l,r=it->r,v=it->v;
	odt.erase(it);
	odt.insert(odtnode(l,pos-1,v));
	return odt.insert(odtnode(pos,r,v)).first;
}

// Assign to same value
inline void assign(int l,int r,int k){
	IT itr=split(r+1),itl=split(l);
	odt.erase(itl,itr);
	odt.insert(odtnode(l,r,k));
}

inline int ci(int l,int r,int k){
	IT itr=split(r+1),itl=split(l);
	int res=0;
	for(;itl!=itr;itl++){
		if(itl->v==k) res+=itl->r-itl->l+1;
	}
	return res;
}

inline void pai(int l,int r){
	int vis[27];
	IT itr=split(r+1),itl=split(l);
	memset(vis,0,sizeof(vis));
	for(IT it=itl;it!=itr;it++){
		vis[it->v]+=it->r-it->l+1;
	}
	odt.erase(itl,itr);
	for(int i=1;i<=26;i++){
		if(vis[i]) odt.insert(odtnode(l,l+vis[i]-1,char(i))),l+=vis[i];
	}
}
Segment Tree code 
1
gg...

注意：此题保证数据随机，因此可以直接用ODT轻松水过（其实也算是一道ODT的模板题了）

千万要记住ODT的Split顺序是先大后小，用完一对指针后这对指针就废了，因此需要一个区间一个区间地处理

ODT code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
int n,m;

#define IT set<odtnode>::iterator
struct odtnode
{
	int l,r;
	mutable ll v;
	odtnode(int L,int R=-1,ll V=0):l(L),r(R),v(V){}
	bool operator <(const odtnode& rhs)const{
		return l<rhs.l;
	}
};
set<odtnode> odt;

inline IT split(int pos){
	IT it=odt.lower_bound(odtnode(pos));
	if(it!=odt.end()&&it->l==pos) return it;
	it--;
	int l=it->l,r=it->r;
	ll v=it->v;
	odt.erase(it);
	odt.insert(odtnode(l,pos-1,v));
	return odt.insert(odtnode(pos,r,v)).first;
}

// Assign to same value
inline void assign(int l,int r,ll k){
	k%=mod;
	IT itr=split(r+1),itl=split(l);
	odt.erase(itl,itr);
	odt.insert(odtnode(l,r,k));
}

// [l,r] + k
inline void add(int l,int r,ll k){
	k%=mod;
	IT itr=split(r+1),itl=split(l);
	for(;itl!=itr;itl++) itl->v=(itl->v+k)%mod;
}

//区间求和
inline ll getsum(int l,int r){
	IT itr=split(r+1),itl=split(l);
	ll res=0;
	for(;itl!=itr;itl++){
		res=((res+itl->v*(itl->r-itl->l+1)%mod)%mod+mod)%mod;
	}
	return res%mod;
}

// 区间拷贝
inline void copy(int l1,int r1,int l2,int r2){
	IT itr1=split(r1+1),itl1=split(l1);
	vector<pair<ll,int>> vec;
	for(IT it=itl1;it!=itr1;it++){
		vec.pb(pair<ll,int>(it->v,it->r-it->l+1));
	}

	IT itr2=split(r2+1),itl2=split(l2);
	odt.erase(itl2,itr2);

	for(vector<pair<ll,int>>::iterator it=vec.begin();it!=vec.end();it++){
		odt.insert(odtnode(l2,l2+it->second-1,it->first));
		l2+=it->second;
	}
}

// 区间交换
inline void exchange(int l1,int r1,int l2,int r2){
	if(l1>l2) swap(l1,l2),swap(r1,r2);
	
	IT itr1=split(r1+1),itl1=split(l1);
	vector<pair<ll,int>> vec1,vec2;
	for(IT it=itl1;it!=itr1;it++){
		vec1.pb(pair<ll,int>(it->v,it->r-it->l+1));
	}
	odt.erase(itl1,itr1);

	IT itr2=split(r2+1),itl2=split(l2);
	for(IT it=itl2;it!=itr2;it++){
		vec2.pb(pair<ll,int>(it->v,it->r-it->l+1));
	}
	odt.erase(itl2,itr2);

	for(vector<pair<ll,int>>::iterator it=vec1.begin();it!=vec1.end();it++){
		odt.insert(odtnode(l2,l2+it->second-1,it->first));
		l2+=it->second;
	}
	for(vector<pair<ll,int>>::iterator it=vec2.begin();it!=vec2.end();it++){
		odt.insert(odtnode(l1,l1+it->second-1,it->first));
		l1+=it->second;
	}
}

// 区间翻转
inline void updown(int l,int r){
	if(l>r) swap(l,r);
	IT itr=split(r+1),itl=split(l);
	vector<pair<ll,int>> vec;
	for(IT it=itl;it!=itr;it++){
		vec.pb(pair<ll,int>(it->v,it->r-it->l+1));
	}
	odt.erase(itl,itr);
	reverse(All(vec));
	for(vector<pair<ll,int>>::iterator it=vec.begin();it!=vec.end();it++){
		odt.insert(odtnode(l,l+it->second-1,it->first));
		l+=it->second;
	}
}

int main(){
	scanf("%d%d",&n,&m);
	int x;
	rep(i,1,n) scanf("%d",&x),odt.insert(odtnode(i,i,x));
	int op,l1,r1,l2,r2,val;
	while(m--){
		scanf("%d%d%d",&op,&l1,&r1);
		if(op==1) printf("%lld\n",getsum(l1,r1));
		if(op==2) scanf("%d",&val),assign(l1,r1,1ll*val);
		if(op==3) scanf("%d",&val),add(l1,r1,1ll*val);
		if(op==4) scanf("%d%d",&l2,&r2),copy(l1,r1,l2,r2);
		if(op==5) scanf("%d%d",&l2,&r2),exchange(l1,r1,l2,r2);
		if(op==6) updown(l1,r1);
	}
	IT itr=split(n+1),itl=split(1);
	for(IT it=itl;it!=itr;it++){
		rep(i,1,it->r-it->l+1){
			printf("%lld ",it->v%mod);
		}
	}
	return 0;
}