树链剖分浅析

树剖专题（长链+重链）

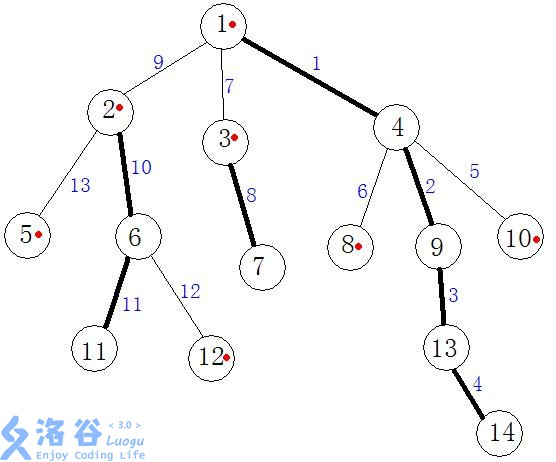
1397737-20180510123640544-303874904

题目链接：P3384 轻重链剖分

简介

树链剖分：顾名思义，把一棵树剖分成为一条条的链（其实就是序列），保证每个点属于且仅属于一条链，然后再通过数据结构（如：树状数组、线段树 等）来维护每一条链的信息，进而维护这一整棵树的信息

那么如何进行剖分呢？ 最常见的剖分方式有两种：轻重链剖分和长链剖分，其中前者更为常用，后者在一些特殊情况下会更优，这里主要讲解前者（后者的处理方式类似）

一些黑话（术语）

  • 重儿子：子树最大的儿子
  • 轻儿子：除了重儿子以外的儿子
  • 重边：父节点与重儿子组成的边
  • 轻边：重边以外的边
  • 重链：重边链接而成的链
  • 轻链：轻边链接而成的链
  • 链的顶部：一条链上深度最小的点

两次DFS的预处理（复杂度$O(n)$）

对于重链剖分，最核心的步骤就是需要预处理出一些东西，包括如下几项：

  1. 每个节点的深度 csdep[i]

  2. 每个节点的父节点 csfa[i]

  3. 每个节点所在的子树大小 cssize[i]（PS：长链剖分则是 最大深度csmx[i]）

  4. 每个节点的重儿子 csson[i]

  5. 每条链的顶部 cstop[i]

如果需要用数据结构维护节点对应的信息，则还需要处理：

  1. 每个节点的DFS序 csid[i]
  2. 每个DFS序对应节点的需要维护的值 wt[i]

第一次DFS（一次性处理完 1 2 3 4）

这里直接给出代码（含注释）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void dfs1(int u,int fath,int depth){
    csfa[u] = fath;// u的父亲
    csdep[u] = depth;// u的深度
    cssize[u] = 1;//u子树的大小，初始为1
    for(auto &&v: e[u]){
        if(v != fath){
            dfs1(v,u,depth+1);//dfs下去，深度+1
            cssize[u] += cssize[v];//此时v都处理完了，加到u的大小上去
            if(cssize[v] > cssize[csson[u]])//判断v的大小能否更新重儿子
                csson[u] = v;//能就更新重儿子
        }
    }
}

dfs1(rt,-1,1);

如果是长链剖分，这里的csize[i]数组就需要换为csmx[i]数组，也就是重儿子的定义从 子树最大的儿子 变为 子树最大深度最深的儿子，所以对应的dfs1函数需要改为：

1
2
3
4
5
6
7
8
void dfs1(...){
    csmx[u] = csdep[u];//初始最大深度
    ...
   	csmx[u] = max(csmx[u],csmx[v]);//维护子树最大深度
    if(csmx[v] > csmx[csson[u]])//重儿子的定义变了
        csson[u] = v;
    ...
}

第二次DFS（处理完剩下的）

第二次DFS有个关键的地方：

  • 需要按照先处理重儿子，再处理轻儿子的顺序
1
2
3
4
5
6
7
8
9
10
11
12
13
void dfs2(int u,int topf){
    csid[u] = ++dfsx;//u的dfs序
    wt[dfsx] = w[u];// 每个dfs序对应节点的需要维护的值（权值、编号 等）
    cstop][u] = topf;//u的顶部
    if(!csson[u]) return;//如果到叶节点了，直接返回
    dfs2(csson[u], topf);//处理重儿子，它的顶部还是当前的顶部
    for(auto &&v: e[u]){
        if(v != csson[u] && v != csfa[u])//处理轻儿子，即除去重儿子和父亲
            dfs(v,v);//轻儿子本身的顶部节点就是自己
    }
}

dfs2(rt,rt);

一些常用操作

至此，树链剖分已经完成了，在不使用数据结构的情况下，我们仍然可以做一些常用操作

求LCA（$O(logn)$）

可以看我的 BlablaWu的blog：最近公共祖先LCA

1
2
3
4
5
6
7
inline int LCA(int x,int y){
    while(cstop[x] != cstop[y]){//只要两者处于不同链
        if(csdep[cstop[x]] < csdep[cstop[y]]) swap(x,y);
        x = csfa[cstop[x]];//不断把更深的点跳到其链顶端的父亲上
    }
    return csdep[x] < csdep[y] ? x : y;//返回较浅的点
}

求树上两点距离（无边权or点权）

答案就是：$x节点深度+y节点深度-2*LCA(x,y)的深度$

1
2
3
inline int getroute(int x,int y){
    return csdep[x] + csdep[y] - (csdep[LCA(x,y)]<<1);
}

求树上两点距离（带边权or点权）

如果是求边权距离的，可以把边权转换为深度较深的节点的点权，并处理出每个节点到根节点的距离，这需要在dfs1过程中处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void dfs1(...){
    ...
   	for(auto &&[w, v]: e[u]){
        if(v!=fath){
            w[v] = e[i].w;//将边权转换为深度较深节点的点权
            // 如果直接给点权了，那就只需要执行下一行
            wdep[v] += w[v];//处理出每个节点到根节点的距离
        }
    }
    ...
}

inline void getroute(int x,int y){//求两点带权距离
    return wdep[x] + wdep[y] - (wdep[LCA(x,y)]<<1);
}

求树上$k$级祖先

模板题：P5903 【模板】树上k级祖先

每次询问给定一个$x$和$k$，求点$x$的$k$级祖先（强制在线）

算法：可以类比树剖LCA的思想，但这里需要求的不是最近的祖先，而是指定的$k$级祖先，因此需要一点思考，对于一个点$x$来说，如果$csdep[x]-k<csdep[cstop[x]]$，也就是说这个$k$级祖先在$x$当前所在链的顶端的上方，那么我们就可以让$x$跳到它所在链顶端的父节点上，然后继续比较，重复上述操作，直到这个$k$级祖先和$x$处在同一条链上，那么又因为同一条链上的节点DFS序是连续增减的，因此可以直接通过作差得出$k$级祖先的DFS序，然后输出这个DFS对应的节点编号就行了

1
2
3
4
5
6
inline int getkans(int x,int k){
    int tp=csdep[x]-k;
    while(tp<csdep[cstop[x]]) x=csfa[cstop[x]];
    tp=csdep[x]-tp;
    return wt[csid[x]-tp];
}

数据结构维护链的信息

如果有的问题是既有修改，又有查询的操作，那么就只好请出我们的数据结构大法了，通常情况下，线段树足以胜任这些要求，下面针对模板题的要求，来介绍一下具体操作方法

  1. 将$x$及其子树的所有节点的点权$+k$
  2. 求出$x$及其子树的所有节点的权值和
  3. 将 $x\rightarrow y$ 路径上的所有节点权值$+k$
  4. 求出 $x\rightarrow y$ 路径上所有点权和

对于 1 2 操作，由于我们维护了每个节点的DFS序以及每个DFS序所对应节点的权值，因此对于一个节点$x$，它所在子树的所有节点的DFS序都比它大，而最大的那个节点的DFS序恰好是csid[x]+cssize[x]-1，中间的所有DFS序就对应了这个子树的所有节点，因此这个操作很简单，如下

1
2
3
4
5
6
7
8
9
// 以x为根的子树权值 + k
void addroot(int x, T k){
    Seg.add_range(1, 1, n, csid[x], csid[x] + cssize[x] - 1, k);
}

// 求以x为根的子树权值和
T getrootsum(int x){
    return Seg.getsum(1, 1, n, csid[x], csid[x] + cssize[x] - 1);
}

对于 3 4 操作，稍微复杂一些，我们可以类比树剖求LCA的思想，先不断跳动链顶较深的节点，期间同时对跳过的每一条链进行更新或求和操作，直到两点在同一条链上，最后再对这一条链上以这两点为端点的区间进行一次操作，具体实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// [x,y] 路径上点权值 + k
void addroute(int x, int y, T k) {
    while (cstop[x] != cstop[y]) {              // 如果不属于同一条重链
        if (csdep[cstop[x]] < csdep[cstop[y]])  // 设x所在链头部较深
            swap(x, y);
        Seg.add_range(1, 1, n, csid[cstop[x]], csid[x], k);
        x = csfa[cstop[x]];  // x跳到所在链头部的父节点上，继续下去
    }
    // 直到x、y在同一重链上
    if (csdep[x] > csdep[y])
        swap(x, y);                             // 设x较浅
    Seg.add_range(1, 1, n, csid[x], csid[y], k);  // 对重链对应区间更新
}

// 求 [x, y] 路径上点权值和
T getroutesum(int x, int y) {
    T res = 0;
    while (cstop[x] != cstop[y]) {
        if (csdep[cstop[x]] < csdep[cstop[y]])
            swap(x, y);
        res += Seg.getsum(1, 1, n, csid[cstop[x]], csid[x]);
        x = csfa[cstop[x]];
    }
    if (csdep[x] > csdep[y])
        swap(x, y);
    res += Seg.getsum(1, 1, n, csid[x], csid[y]);
    return res;
}

至此，树链剖分的基本操作就介绍完毕了，剩下的就是一堆习题了，当然我还没做，等做完了再过来补吧 Orz