最近公共祖先LCA

最近公共祖先LCA的各种算法总结

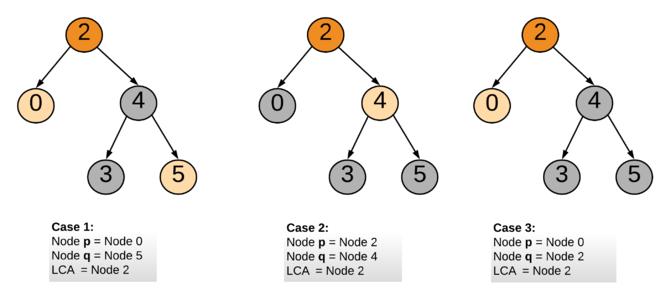
u=1365587845,1055642733&fm=26&gp=0

LCA（最近公共祖先）

模板题链接：最近公共祖先（LCA）

LCA（最近公共祖先），顾名思义，就是一棵树中两个节点的一个公共的祖先，而这个祖先距离这两个节点是最近的

关于求LCA的算法，前人已经总结出了很多种，大致分为以下几种：

暴力求LCA（舍弃）
倍增算法求LCA
Tarjan算法求LCA（离线）
树链剖分求LCA

这里逐一记录一下

暴力求LCA

暴力算法不难想到，对于两个节点的LCA，我们可以先从一个节点出发，（一步一步地）标记出他到达根节点所走过的路径上的所有节点，再从另一个节点出发（一步一步地）往根节点走，走到过的第一个被标记过的节点就是他们俩的LCA，对于有n个节点和q次询问的树，时间复杂度为：$O(nq)$~~（太鸡儿慢了）~~

倍增求LCA

关于倍增算法，已经再熟悉不过了，Vector的实现、ST表等，都是利用的倍增思想，将复杂度由线性级别转变为对数级别，是一个非常实用的优化算法思想

对于倍增求LCA，其实它就是暴力求LCA算法的一个优化（咱们不要一步一步往上爬，咱们一次跨$2^i$步），它是一个预处理+在线询问的算法，预处理复杂度为$O(nlogn)$，一次询问的复杂度为$O(logn)$，所以对于q次询问的操作来说，总复杂度为：$O(nlogn + qlogn)$

我们可以考虑开一个fa[i][j]数组，存储这棵树的第$i$号节点的第$2^{j}$个父亲，利用二进制的优势是倍增算法的核心，这样一来，我们可以利用一个简单的DP方程来完成这个数组的预处理过程：首先我们可以通过一趟DFS（或者BFS）得到对于每个节点$i$的对应fa[i][0]的值（即每个节点的直接父亲节点），以及每个节点的深度（depth）

void dfs(int u){
    vis[u]=1;//这个节点设置为走过
    for(int i=head[u];~i;i=e[i].next){
        int v=e[i].v;
        if(!vis[v]){
            dep[v]=dep[u]+1;//深度+1
            fa[v][0]=u;//求出直接父亲
            dfs(v);//递归
        }
    }
}

然后通过如下转移方程即可完成状态转移（倍增求LCA的核心1）：

$fa[i][j]=fa[fa[i][j-1]][j-1]\\ 因为：2^j=2^{j-1}\cdot2^{j-1}$

inline void init_lca(){
    for(int i=1;i<=20;i++){
    //这里的20是一个上界的大致值（一般够用），其实应该等于log2(maxdepth)
        for(int j=1;j<=n;j++){//枚举树的节点数n
            fa[j][i]=fa[fa[j][i-1]][i-1];//状态转移
        }
    }
}

预处理完毕了，接下来就是求LCA的操作了（倍增求LCA的核心2）：对于两个节点$x,y$来说，假设dep[x]>dep[y]，我们需要先让两个节点的深度达到一致（先让更深的节点x不断往父节点跳，一次跳$\log_2(dep[x]-dep[y])$的距离），此时需要特判一下是否x和y就已经重合了，如果是，那说明这次询问的y就是x和y的LCA，直接返回即可，否则执行下一步：此后，再让x和y同时往上跳，只要每一刻他们的第$2^{i-1}$个父节点不一样，他们就可以跳到第$2^{i-1}$个父节点的位置成为这个父节点，循环下去，挑出循环后，由于此时x和y还未重合成为他们的LCA，但他们都只离LCA只有1个节点的距离（也就是说他们的LCA就是他们的直接父亲节点），因此最后的答案就是fa[x][0]（当然fa[y][0]也一样）

inline int LCA(int x,int y){
    if(dep[x]<dep[y]) swap(x,y);//把x调为最深的一个
    while(dep[x]>dep[y])
        x=fa[x][int(log2(dep[x]-dep[y]))];
    if(x==y) return x;//y就是x、y的LCA
    for(int i=log2(dep[x]);i>=0;i--)//从x的深度的log2开始枚举
        if(fa[x][i]!=fa[y][i])//如果他们俩的该倍父亲不相等
            x=fa[x][i],y=fa[y][i];//跳到这个父亲的位置上，继续循环下去
    return fa[x][0];//返回直接父亲
}

当然，倍增LCA由于其独有的预处理操作（很像线段树的push_up操作），可以支持维护很多具有结合律的东西，如两节点间的最值、边权之和、点权之和等，比较灵活

倍增求LCA模板代码：

code

//略去头文件
//倍增LCA核心部分
int n,m,s,fa[maxn][21],dep[maxn],cnt,head[maxn];
bool vis[maxn];
inline void dfs(int u){
	vis[u]=1;
	for(int i=head[u];~i;i=e[i].next){
		int v=e[i].v;
		if(!vis[v]){
			fa[v][0]=u;
			dep[v]=dep[u]+1;
			dfs(v);
		}
	}
}
inline int LCA(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);
	while(dep[x]>dep[y]){
		x=fa[x][int(log2(dep[x]-dep[y]))];
	}
	if(x==y) return x;
	for(int i=log2(dep[x]);i>=0;i--){
		if(fa[x][i]!=fa[y][i]){
			x=fa[x][i],y=fa[y][i];
		}
	}
	return fa[x][0];
}
int main(){
	n=read(),m=read(),s=read();
	init();
	int x,y;
	rep(i,1,n-1){
		x=read(),y=read();
		addedge(x,y);
		addedge(y,x);
	}
	dfs(s);
	rep(i,1,20){
		rep(j,1,n){
			fa[j][i]=fa[fa[j][i-1]][i-1];
		}
	}
	rep(i,1,m){
		x=read(),y=read();
		write(LCA(x,y)),putchar('\n');
	}
	return 0;
}

Tarjan算法求LCA（离线）

对于Tarjan算法，早在SCC（强连通分量）专题就已经有所耳闻了，但没想到的是它居然还能用来求LCA？！（Tarjan简直太巨了！%%%）

Tarjan求LCA是一种并査集维护+Tarjan离线处理的算法，由于并査集路径压缩具有近似于$O(1)$的复杂度，因此对于具有q次询问的操作，Tarjan求LCA的复杂度为：$O(q+n)$，可以说是非常优秀的离线算法了

核心思想：从根节点开始DFS每一个出边所连的节点，标记访问过，同时将u节点出边所连的节点v全部用并査集合并到其父亲u上，处理完一个节点的所有出边后，再遍历与该节点u相关联的每一个询问（用类似前向星的链表存储询问中两节点的关联，即再对询问建一个图），如果当前询问所关联的节点to已经被访问过了，则这个询问所对应的两个节点的LCA就是find(to)（证明略，其实就是利用的dfs回溯的特点，与Tarjan求SCC很像）

PS：并査集切记要初始化！！！

inline void TarjanLCA(int u){//Tarajn求LCA
	vis[u]=1;//标记过
	for(int i=head[u];~i;i=e[i].next){
		int v=e[i].v;
		if(!vis[v]){
			TarjanLCA(v);//dfs下去
			Fa[find(v)]=u;//合并到父亲上
		}
	}
	for(int i=headq[u];~i;i=q[i].next){//遍历每个相关的询问
		int to=q[i].to;
		if(vis[to]){//如果关联节点访问过
			ans[q[i].id]=find(to);//则LCA可直接得出，记得存到对应标号的答案里
		}
	}
}

Tarjan求LCA模板代码

code

int n,m,s,cnt,head[maxn];
int headq[maxn],qcnt,ans[maxn];
bool vis[maxn];
struct Q//询问的结构体
{
	int to,next,id;
}q[maxn];
inline void TarjanLCA(int u){
	vis[u]=1;
	for(int i=head[u];~i;i=e[i].next){
		int v=e[i].v;
		if(!vis[v]){
			TarjanLCA(v);
			Fa[find(v)]=u;
		}
	}
	for(int i=headq[u];~i;i=q[i].next){
		int to=q[i].to;
		if(vis[to]){
			ans[q[i].id]=find(to);
		}
	}
}
int main(){
	n=read(),m=read(),s=read();
	init();
	int x,y;
	rep(i,1,n-1){
		x=read(),y=read();
		addedge(x,y);
		addedge(y,x);
	}
	rep(i,1,m){
		x=read(),y=read();
		addask(x,y,i);
		addask(y,x,i);
	}
	TarjanLCA(s);
	rep(i,1,m) write(ans[i]),putchar('\n');
	return 0;
}

树链剖分求LCA

终于轮到我们的树上操作の终极大杀器：树链剖分 登场了

树链剖分，顾名思义，就是将一棵树剖分成为一条一条的链（也就是序列），然后可以通过某种方式（通常为线段树）维护这一条条链的信息，那么也就成功维护了整棵树的信息了（详情见我的树链剖分专题，这里直接谈简单的树剖LCA）

树剖求LCA的方法类似于树上区间修改的操作，具体说来如下：对于一棵树上的两个点$x,y$，假设$x$所在链的顶端深度较深，则直接将$x$跳到它所在链的顶端的父亲节点，如此循环，直到$x,y$两点到达同一条链上，此时直接输出两者中深度较浅的节点的编号即可（这个节点就是$x,y$的LCA）

时间复杂度：$O(n)$剖分预处理，最坏$O(logn)$查询

code

//略去头文件和一些模板
//树剖LCA
int n,m,r,x,y;
int dfsx,csdep[maxn],csid[maxn],csfa[maxn],csson[maxn],cstop[maxn],cssize[maxn];

// 第一次dfs：处理出 深度、父亲、子树大小、重儿子
inline void dfs1(int u,int fath,int depth){
	csdep[u]=depth;
	csfa[u]=fath;
	cssize[u]=1;
	int maxsize=-1;
	for(int i=head[u];~i;i=e[i].next){
		int v=e[i].v;
		if(v!=fath){
			dfs1(v,u,depth+1);
			cssize[u]+=cssize[v];
			if(cssize[v]>maxsize)
				maxsize=cssize[v],csson[u]=v;
		}
	}
}

// 第二次dfs：求出dfs序、dfs序对应初始值、节点所在链的顶端
inline void dfs2(int u,int topf){
	csid[u]=++dfsx;
	cstop[u]=topf;
	if(!csson[u]) return;
	dfs2(csson[u],topf);
	for(int i=head[u];~i;i=e[i].next){
		int v=e[i].v;
		if(v!=csfa[u]&&v!=csson[u]){
			dfs2(v,v);
		}
	}
}
// 树剖LCA核心操作
inline int LCA(int x,int y){
	while(cstop[x]!=cstop[y]){
        //每次跳所在链顶端更深的节点
		if(csdep[cstop[x]]<csdep[cstop[y]]) swap(x,y);
		x=csfa[cstop[x]];
	}
	return csdep[x]<csdep[y]?x:y;
}

int main(){
	n=read(),m=read(),r=read();
	init();
	rep(i,1,n-1){
		x=read(),y=read();
		addedge(x,y);
		addedge(y,x);
	}
    //树剖预处理：两次dfs
	dfs1(r,-1,1);
	dfs2(r,r);
	rep(i,1,m){
		x=read(),y=read();
		write(LCA(x,y)),putchar('\n');
	}
	return 0;
}

知识点：树上差分

参考blog：树上差分详解

这里记录一个比较常用的树上操作：树上差分，顾名思义，就是在树上进行差分操作和DFS求前缀和操作，实现复杂度优化，具体实现如下（很好理解，就不给证明了）

点差分

将两点$u,v$之间路径上所有点权增加$x$，则操作如下：

1	`diff[u]+=x,diff[v]+=x,diff[LCA(u,v)]-=x,diff[fa[LCA(u,v)]]-=x;`

边差分

将两点$u,v$之间路径上所有边权增加$x$，则操作如下：

1	`diff[u]+=x,diff[v]+=x,diff[LCA(u,v)]-=2*x;`

求树上前缀和

int dfs(int u,int fath){
    for(int i=head[u];~i;i=e[i].next){
        int v=e[i].v;
        if(v!=fath)
            presum[u]+=dfs(v,u);
    }
    return presum[u];
}

树上差分模板题：P3128 Max Flow P

code

const int N=500005,M=500005;
struct Edge{
	int u,v,w,next;
}e[M<<1];
int n,k,cnt,head[N],tdiff[N];
inline void init(){
	cnt=0;
	memset(head,-1,sizeof(head));
}
inline void addedge(int u,int v,int w=0){
	e[cnt]=Edge{u,v,w,head[u]};
	head[u]=cnt++;
}
int vis[N],fa[N][21],dep[N],ans;
void lcadfs(int u){
	vis[u]=1;
	for(int i=head[u];~i;i=e[i].next){
		int v=e[i].v;
		if(!vis[v]){
			fa[v][0]=u;
			dep[v]=dep[u]+1;
			lcadfs(v);
		}
	}
}
void init_lca(){
	rep(i,1,20){
		rep(j,1,n){
			fa[j][i]=fa[fa[j][i-1]][i-1];
		}
	}
}
inline int LCA(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);
	while(dep[x]>dep[y]) x=fa[x][int(log2(dep[x]-dep[y]))];
	if(x==y) return x;
	for(int i=log2(dep[x]);i>=0;i--){
		if(fa[x][i]!=fa[y][i]){
			x=fa[x][i],y=fa[y][i];
		}
	}
	return fa[x][0];
}
int dfs(int u,int fath){
	for(int i=head[u];~i;i=e[i].next){
		int v=e[i].v;
		if(v!=fath){
			tdiff[u]+=dfs(v,u);
		}
	}
	ans=max(ans,tdiff[u]);
	return tdiff[u];
}
int main(){
	scanf("%d%d",&n,&k);
	init();
	int x,y;
	rep(i,1,n-1) scanf("%d%d",&x,&y),addedge(x,y),addedge(y,x);
	lcadfs(1);
	init_lca();
	rep(i,1,k){
		scanf("%d%d",&x,&y);
		int lca=LCA(x,y);
		tdiff[y]++;
		tdiff[x]++;
		tdiff[lca]--;
		tdiff[fa[lca][0]]--;
	}
	dfs(1,-1);
	printf("%d\n",ans);
	return 0;
}

习题汇总

P1967 货车运输（最大生成树建树+LCA求最小值）

code

// 略去头文件
int n,m,q,Fa[maxn],fa[maxn][21],w[maxn][21],dep[maxn],cnt1,cnt2,head1[maxn],head2[maxn];
bool vis[maxn];
inline int find(int x){return x==Fa[x]?x:Fa[x]=find(Fa[x]);}
struct Edge
{
	int u,v,w,next;
}e1[maxn<<1],e2[maxn<<1];
bool cmp(Edge x1,Edge x2){
	return x1.w>x2.w;
}
inline void addedge1(int u,int v,int w=0){
	e1[++cnt1]=Edge{u,v,w,head1[u]};
	head1[u]=cnt1;
}
inline void addedge2(int u,int v,int w=0){
	e2[++cnt2]=Edge{u,v,w,head2[u]};
	head2[u]=cnt2;
}
inline void init(){
	rep(i,1,n) Fa[i]=i;
	cnt1=cnt2=0;
}
inline void dfs(int u){
	for(int i=head2[u];i;i=e2[i].next){
		int v=e2[i].v;
		if(!vis[v]){
			vis[v]=1;
			dep[v]=dep[u]+1;
			fa[v][0]=u;
			w[v][0]=e2[i].w;
			dfs(v);
		}
	}
}

inline int LCAmin(int x,int y){
	if(find(x)!=find(y)) return -1;
	int ans=inf;
	if(dep[x]<dep[y]) x^=y^=x^=y;
	while(dep[x]>dep[y]){
		ans=min(ans,w[x][int(log2(dep[x]-dep[y]))]);
		x=fa[x][int(log2(dep[x]-dep[y]))];
	}
	if(x==y) return ans;
	for(int i=log2(dep[x]);i>=0;i--){
		if(fa[x][i]!=fa[y][i]){
			ans=min(ans,min(w[x][i],w[y][i]));
			x=fa[x][i],y=fa[y][i];
		}
	}
	return min(ans,min(w[x][0],w[y][0]));
}

inline void kruskal(){
	init();
	sort(e1+1,e1+1+m,cmp);
	for(int i=1;i<=m;i++){
		int eu=find(e1[i].u),ev=find(e1[i].v);
		if(eu!=ev){
			Fa[eu]=ev;
			addedge2(e1[i].u,e1[i].v,e1[i].w);
			addedge2(e1[i].v,e1[i].u,e1[i].w);
		}
	}
}
int main(){
	// freopen("P1967_1.in","r",stdin);
	scanf("%d%d",&n,&m);
	int x,y,z;
	rep(i,1,m){
		scanf("%d%d%d",&x,&y,&z);
		addedge1(x,y,z);
	}
	kruskal();
	for(int i=1;i<=n;i++){
		if(!vis[i]){
			vis[i]=1;
			dfs(i);
		}
	}
	for(int i=1;i<=20;i++){
		for(int j=1;j<=n;j++){
			fa[j][i]=fa[fa[j][i-1]][i-1];
			w[j][i]=min(w[j][i-1],w[fa[j][i-1]][i-1]);
		}
	}
	scanf("%d",&q);
	rep(i,1,q){
		scanf("%d%d",&x,&y);
		printf("%d\n",LCAmin(x,y));
	}
	return 0;
}

P2680 运输计划（树上差分+二分答案+树剖LCA，倍增LCA似乎会T）

code

// 略去头文件
int n,m,lcafa[maxn][25],sum[maxn][25],head[maxn],dep[maxn],LG[maxn],cnt;
int longest,dfscnt,treediff[maxn],sta[maxn],top;
struct Edge
{
	int u,v,w,next;
}e[maxn<<1];
struct Q
{
	int u,v,lca,routesum;
}q[maxn];
inline void addedge(int u,int v,int w=0){
	e[cnt]=Edge{u,v,w,head[u]};
	head[u]=cnt++;
}
void dfs1(int u,int fath){
	for(int i=head[u];~i;i=e[i].next){
		int v=e[i].v,w=e[i].w;
		if(v!=fath){
			dep[v]=dep[u]+1;
			lcafa[v][0]=u;
			sum[v][0]=w;
			dfs1(v,u);
		}
	}
}

inline int LCA(int x,int y,int &Sum){
	if(dep[x]<dep[y]) swap(x,y);
	while(dep[x]>dep[y]){
		Sum+=sum[x][LG[dep[x]-dep[y]]];
		x=lcafa[x][LG[dep[x]-dep[y]]];
	}
	if(x==y) return x;
	for(int i=LG[dep[x]];i>=0;i--){
		if(lcafa[x][i]!=lcafa[y][i]){
			Sum+=sum[x][i]+sum[y][i];
			x=lcafa[x][i];
			y=lcafa[y][i];
		}
	}
	Sum+=sum[x][0]+sum[y][0];
	return lcafa[x][0];
}

inline int dfs2(int u,int fath){
	for(int i=head[u];~i;i=e[i].next){
		int v=e[i].v;
		if(v!=fath){
			treediff[u]+=dfs2(v,u);
		}
	}
	if(treediff[u]==dfscnt){
		sta[++top]=sum[u][0];
	}
	return treediff[u];
}

inline bool check(int x){
	memset(treediff,0,sizeof(treediff));
	int maxh=0;
	dfscnt=0;
	rep(i,1,m){
		if(q[i].routesum>x){//树上差分
			dfscnt++;
			treediff[q[i].u]++;
			treediff[q[i].v]++;
			treediff[q[i].lca]-=2;
		}
	}
	dfs2(1,0);
	while(top){
		maxh=max(maxh,sta[top--]);
	}
	return longest-maxh>x;
}

int main(){
	// freopen("P2680_13.in","r",stdin);
	n=read(),m=read();
	memset(head,-1,sizeof(head));
	for(int i=1,u,v,w;i<n;i++){
		u=read(),v=read(),w=read();
		addedge(u,v,w);
		addedge(v,u,w);
	}

	rep(i,1,n) LG[i]=log2(i);
	dfs1(1,0);
	rep(i,1,24){
		rep(j,1,n){
			lcafa[j][i]=lcafa[lcafa[j][i-1]][i-1];
			sum[j][i]=sum[j][i-1]+sum[lcafa[j][i-1]][i-1];
		}
	}
	rep(i,1,m){
		q[i].u=read(),q[i].v=read();
		q[i].lca=LCA(q[i].u,q[i].v,q[i].routesum);
		longest=max(longest,q[i].routesum);
	}

	int l=0,r=longest;
	while(l<=r){//二分答案
		int mid=(l+r)>>1;
		if(check(mid)) l=mid+1;
		else r=mid-1;
	}
	write(l),putchar('\n');
	return 0;
}

逃不掉的路（E-DCC缩点建树+LCA求树上两点距离）

code

// 忽略头文件
const int maxn=500005;
const int N=500005,M=2*500005;
struct Edge{
	int u,v,w,next;
}e1[M<<1],e2[M<<1];
int cnt1,head1[N],cnt2,head2[N];
int n,m,q;
int low[maxn],dfn[maxn],sta[maxn],vis[maxn],color[maxn],top,scc,deep;
int fa[maxn][21],dist[maxn][21],dep[maxn];
inline void init(){
	cnt1=cnt2=0;
	memset(head1,-1,sizeof(head1));
	memset(head2,-1,sizeof(head2));
}
inline void addedge1(int u,int v,int w=0){
	e1[cnt1]=Edge{u,v,w,head1[u]};
	head1[u]=cnt1++;
}
inline void addedge2(int u,int v,int w=0){
	e2[cnt2]=Edge{u,v,w,head2[u]};
	head2[u]=cnt2++;
}

inline void tarjan(int u,int fath){//tarjan缩点
	vis[sta[++top]=u]=1;
	low[u]=dfn[u]=++deep;
	for(int i=head1[u];~i;i=e1[i].next){
		int v=e1[i].v;
		if(v==fath) continue;
		// if(i==(fath^1)) continue;
		if(!dfn[v]){
			tarjan(v,u);
			low[u]=min(low[u],low[v]);
		}else if(vis[v]) low[u]=min(low[u],dfn[v]);
	}
	if(dfn[u]==low[u]){
		vis[u]=0;
		color[u]=++scc;
		while(sta[top]!=u){
			vis[sta[top]]=0;
			color[sta[top--]]=scc;
		}
		top--;
	}
}

inline void dfs(int u){
	vis[u]=1;
	for(int i=head2[u];~i;i=e2[i].next){
		int v=e2[i].v;
		if(!vis[v]){
			dep[v]=dep[u]+1;
			fa[v][0]=u;
			dist[v][0]=1;
			dfs(v);
		}
	}
}

inline int LCA(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);
	int ans=0;
	while(dep[x]>dep[y]){
		ans+=dist[x][int(log2(dep[x]-dep[y]))];
		x=fa[x][int(log2(dep[x]-dep[y]))];
	}
	if(x==y) return ans;
	for(int i=log2(dep[x]);i>=0;i--){
		if(fa[x][i]!=fa[y][i]){
			ans+=dist[x][i]+dist[y][i];
			x=fa[x][i],y=fa[y][i];
		}
	}
	ans+=dist[x][0]+dist[y][0];
	return ans;
}

int main(){
	scanf("%d%d",&n,&m);
	init();
	rep(i,1,m){
		int u,v;
		scanf("%d%d",&u,&v);
		addedge1(u,v,1);
		addedge1(v,u,1);
	}

	rep(i,1,n) if(!dfn[i]) tarjan(i,-1);

	rep(u,1,n){
		for(int i=head1[u];~i;i=e1[i].next){
			int v=e1[i].v;
			if(color[u]!=color[v]){
				addedge2(color[u],color[v],1);
			}
		}
	}
	// rep(i,1,n) printf("%d scc:%d\n",i,color[i]);
	memset(vis,0,sizeof(vis));
	dfs(1);
	rep(i,1,20){
		rep(j,1,scc){
			fa[j][i]=fa[fa[j][i-1]][i-1];
			dist[j][i]=dist[j][i-1]+dist[fa[j][i-1]][i-1];
		}
	}

	scanf("%d",&q);
	rep(i,1,q){
		int x,y;
		scanf("%d%d",&x,&y);
		printf("%d\n",LCA(color[x],color[y]));
	}
	return 0;
}

算法

LCA 倍增树链剖分 Tarjan

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

科普知识：冷却塔为什么是曲面的？上一篇

莫队算法下一篇