优雅的暴力:分块应用の莫队算法
参考blog:
莫队算法,众所周知,它是由莫涛大神提出的,一种玄学毒瘤暴力的区间操作算法,它的应用结合了分块的特点,以及排序的优化玄学,最终达到根号级别的复杂度,十分可观
前置姿势:
- 分块的基本思想
- STL的排序(自定义排序)
- 基础卡常技巧
- 倍增/树剖 求LCA
- 数值离散化
普通莫队
先看下这题:D-query,当然HH的项链这题也可,但是它SB居然卡莫队

每次询问区间内不同数字的个数,这是普通莫队最简单的模板题,其算法思路大概是这样的:(下面是莫队的基本思想)
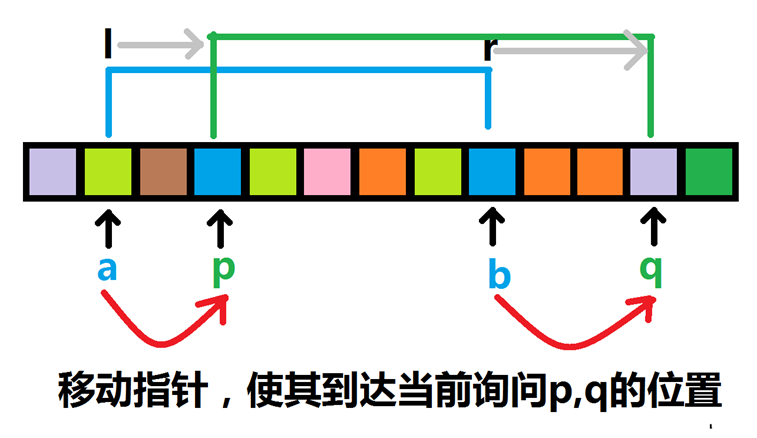
应用双指针方法,每次询问的时候将指针一步一步地移动至对应的左右端点,移动时同步更新区间内的值出现的次数(开一个数组存储即可),具体实现如下
| rep(i,1,m){
int tl=q[i].l,tr=q[i].r;
while(l<tl) del(l++);
while(l>tl) add(--l);
while(r<tr) add(++r);
while(r>tr) del(r--);
ans[q[i].id]=now;
}
|
而其中的add函数和del函数如下,也就是说:对于每次转移区间,我们要对应地将之前一次询问的左右端点移至当前询问的左右端点,期间如果是删除元素,则执行删除操作,如果出现了删完之后该值的出现次数为0,则对应区间的元素总个数-1,同理,如果是添加元素,则执行添加操作,如果添加之前该元素的出现次数为0,则对应区间的元素总个数要+1(因为把这个新元素添加进来了)
| inline void del(int pos){
--cnt[a[pos]];
if(!cnt[a[pos]]) --now;
}
inline void add(int pos){
if(!cnt[a[pos]]) ++now;
++cnt[a[pos]];
}
|
然而,仅仅这么做还不够,因为如果我们的询问区间长这样:

那么这两个指针将会在整个区间两头反复横跳,这样的算法就会比暴力还慢(多了个常数),所以我们要考虑优化这个算法,
接下来就是莫队算法的玄学核心思想:对序列分块(此题分成$\sqrt{n}$最优),并将询问的区间排序(将询问存到结构体里,第一关键字为左端点所在块,第二关键字为右端点),也就是说,左端点所在块小的优先处理,左端点同在一块中则右端点小的优先处理,这样一来,复杂度大大下降了(但是是离线的操作),可以简单证明如下:
对于每一个块内询问,其右端点可能的最大跳动范围为整个序列(n),而总共有$\sqrt{n}$个块,因此总复杂度为$O(n\sqrt{n})$
排序操作如下:
| bool cmp(Q x1,Q x2){
if(bel[x1.l]==bel[x2.l]) return x1.r<x2.r;
return bel[x1.l]<bel[x2.l];
}
|
至此,这题就被我们完美地解决了(最后记得要按照题目输入的顺序输出答案)
但是,实际上还可以在常数上做一些改进(快读之类的我就不说了):奇偶性排序
对于上面的排序函数,我们将其改写成如下形式:
| bool cmp(Q x1,Q x2){
return bel[x1.l]^bel[x2.l]?bel[x1.l<bel[x2.l]:((bel[x1.l]&1)?x1.r<x2.r:x1.r>x2.r)
}
|
翻译过来就是:对于左端点所在块相同的询问,当左端点所在块为奇数块则按照右端点升序排序,否则按照右端点降序排序
而其优化的原理大概还是尽量减少了指针跳动的幅度:当我们处理完了奇数块时,此时右端点指针在最右断,下一块轮到偶数块了,我们就不需要把右端点从最右端挪到最左端来重新从左往右跳动了,而是直接从右往左跳动,使得每个来回跳动的操作都是尽量有效的操作
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
int n,m,a[30005],blk,st[30005],en[30005],bel[30005],now;
int ans[200005],cnt[1000005];
struct Q{
int l,r,id;
}q[200005];
bool cmp(Q x1,Q x2){
if(bel[x1.l]==bel[x2.l]) return bel[x1.r]<bel[x2.r];
return bel[x1.l]<bel[x2.l];
}
inline void init_blk(int n){
blk=sqrt(n);
rep(i,1,blk){
st[i]=n/blk*(i-1)+1;
en[i]=n/blk*i;
}
en[blk]=n;
rep(i,1,blk){
rep(j,st[i],en[i]){
bel[j]=i;
}
}
}
inline void del(int pos){
--cnt[a[pos]];
if(!cnt[a[pos]]) --now;
}
inline void add(int pos){
if(!cnt[a[pos]]) ++now;
++cnt[a[pos]];
}
int main(){
scanf("%d",&n);
rep(i,1,n) scanf("%d",&a[i]);
init_blk(n);
scanf("%d",&m);
rep(i,1,m){
scanf("%d%d",&q[i].l,&q[i].r);
q[i].id=i;
}
sort(q+1,q+1+m,cmp);
int l=1,r=0;
rep(i,1,m){
int tl=q[i].l,tr=q[i].r;
while(l<tl) del(l++);
while(l>tl) add(--l);
while(r<tr) add(++r);
while(r>tr) del(r--);
ans[q[i].id]=now;
}
rep(i,1,m) printf("%d\n",ans[i]);
return 0;
}
|
莫队算法的注意事项和重点:
- 莫队算法优秀的根号复杂度是建立在每次修改操作(对应上题就是del和add操作)的复杂度是非常小的(O(1))基础上的,因此,如果对应的修改操作复杂度非常大的话,莫队还是很慢的QAQ
- 莫队算法是一个离线算法(因为他要排序),如果题目要强制在线了,那就可以和莫队说拜拜了
普通莫队习题:
D-query(普通莫队,询问区间不同的数的个数)
小B的询问(普通莫队,询问区间每个数出现次数的平方和)
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
int n,m,k,blk,a[maxn],cnt[maxn],st[maxn],en[maxn],bel[maxn];
ll Ans[maxn];
struct Q
{
int l,r,id;
}q[maxn];
bool cmp(Q x1,Q x2){
if(bel[x1.l]==bel[x2.l]) return bel[x1.r]<bel[x2.r];
return bel[x1.l]<bel[x2.l];
}
inline void init_blk(){
blk=sqrt(n);
rep(i,1,blk)
st[i]=n/blk*(i-1)+1,en[i]=n/blk*i;
en[blk]=n;
rep(i,1,blk){
rep(j,st[i],en[i]){
bel[j]=i;
}
}
}
int main(){
scanf("%d%d%d",&n,&m,&k);
rep(i,1,n) scanf("%d",&a[i]);
init_blk();
rep(i,1,m) scanf("%d%d",&q[i].l,&q[i].r),q[i].id=i;
sort(q+1,q+1+m,cmp);
int l=1,r=0;
ll ans=0;
rep(i,1,m){
int tl=q[i].l,tr=q[i].r;
while(l<tl) --cnt[a[l]],ans-=2*cnt[a[l]]+1,l++;
while(l>tl) l--,++cnt[a[l]],ans+=2*cnt[a[l]]-1;
while(r<tr) r++,++cnt[a[r]],ans+=2*cnt[a[r]]-1;
while(r>tr) --cnt[a[r]],ans-=2*cnt[a[r]]+1,r--;
Ans[q[i].id]=ans;
}
rep(i,1,m) printf("%lld\n",Ans[i]);
return 0;
}
|
大爷的字符串题(普通莫队,询问区间众数的出现次数)
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
int n,m,blk,a[maxn],b[maxn],st[maxn],en[maxn],bel[maxn],cnt[maxn],ge[maxn];
ll Ans[maxn],ans;
struct Q
{
int l,r,id;
}q[maxn];
bool cmp(Q x1,Q x2){
return bel[x1.l]^bel[x2.l]?bel[x1.l]<bel[x2.l]:((bel[x1.l]&1)?x1.r<x2.r:x1.r>x2.r);
}
inline void init_blk(){
blk=sqrt(n);
rep(i,1,blk) st[i]=n/blk*(i-1)+1,en[i]=n/blk*i;
en[blk]=n;
rep(i,1,blk){
rep(j,st[i],en[i]) bel[j]=i;
}
sort(b+1,b+1+n);
int len=unique(b+1,b+1+n)-b-1;
rep(i,1,n){
a[i]=lower_bound(b+1,b+1+len,a[i])-b;
}
}
inline void add(int pos){
--ge[cnt[a[pos]]];
++cnt[a[pos]];
++ge[cnt[a[pos]]];
ans=max(ans,1ll*cnt[a[pos]]);
}
inline void del(int pos){
if(cnt[a[pos]]==ans&&ge[cnt[a[pos]]]==1) ans--;
--ge[cnt[a[pos]]];
--cnt[a[pos]];
++ge[cnt[a[pos]]];
}
int main(){
scanf("%d%d",&n,&m);
rep(i,1,n) scanf("%d",&a[i]),b[i]=a[i];
init_blk();
rep(i,1,m) scanf("%d%d",&q[i].l,&q[i].r),q[i].id=i;
sort(q+1,q+1+m,cmp);
int l=1,r=0;
rep(i,1,m){
int tl=q[i].l,tr=q[i].r;
while(l<tl) del(l++);
while(l>tl) add(--l);
while(r<tr) add(++r);
while(r>tr) del(r--);
Ans[q[i].id]=-ans;
}
rep(i,1,m) printf("%lld\n",Ans[i]);
return 0;
}
|
faebdc的烦恼(同上)
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
int n,m,st[maxn],en[maxn],bel[maxn],blk,cnt[maxn],ge[maxn],a[maxn],ans[maxn],now;
struct que
{
int l,r,id;
}q[maxn];
bool cmp(que x1,que x2){
return bel[x1.l]==bel[x2.l]?bel[x1.r]<bel[x2.r]:bel[x1.l]<bel[x2.l];
}
inline void init_blk(){
blk=sqrt(n);
rep(i,1,blk) st[i]=n/blk*(i-1)+1,en[i]=n/blk*i;
en[blk]=n;
rep(i,1,blk)
rep(j,st[i],en[i])
bel[j]=i;
}
inline void add(int pos){
--ge[cnt[a[pos]]];
++cnt[a[pos]];
++ge[cnt[a[pos]]];
now=max(now,cnt[a[pos]]);
}
inline void del(int pos){
if((now==cnt[a[pos]])&&(ge[cnt[a[pos]]]==1)) now--;
--ge[cnt[a[pos]]];
--cnt[a[pos]];
++ge[cnt[a[pos]]];
}
int main(){
scanf("%d%d",&n,&m);
rep(i,1,n) scanf("%d",&a[i]);
init_blk();
rep(i,1,m) scanf("%d%d",&q[i].l,&q[i].r),q[i].id=i;
sort(q+1,q+1+m,cmp);
int l=1,r=0;
rep(i,1,m){
int tl=q[i].l,tr=q[i].r;
while(l<tl) del(l++);
while(l>tl) add(--l);
while(r<tr) add(++r);
while(r>tr) del(r--);
ans[q[i].id]=now;
}
rep(i,1,m) printf("%d\n",ans[i]);
return 0;
}
|
带修莫队
那么就不得不提到带修改莫队的模板题了:国家集训队 数颜色/维护队列
这道题其实就是加入了单点修改的上一道题,因此看上去这道题是一个在线的题,而且莫队不支持在线操作,那么如何实现带修改的莫队呢?
我们可以在普通莫队的基础上,将查询操作和修改操作分开记录,并使用一个时间戳变量来记录每次查询操作所对应的最近的前一次修改操作,具体实现如下:
| struct Q{
int l,r,time;
}q[maxn];
struct mo{
int pos,val;
}mo[maxn];
|
对于排序操作,由于多加了一个时间戳变量(而这恰恰又是最耗时间的操作),我们这么安排排序规则:第一关键字为左端点所在块,第二关键字为右端点所在块,第三关键字为时间戳,都设置为升序排序,这样一来,复杂度又得到了优化
| bool cmp(que x1,que x2){
if(bel[x1.l]==bel[x2.l]&&bel[x1.r]==bel[x2.r]) return x1.tim<x2.tim;
if(bel[x1.l]==bel[x2.l]) return bel[x1.r]<bel[x2.r];
return bel[x1.l]<bel[x2.l];
}
|
另外,这道题经过大佬的证明,可以得出当块的大小为$n^{frac{2}{3}}$时(即共有$n^{frac{1}{3}}$个块)可以达到$O(n^{frac{5}{3}})$的复杂度,要优于块大小为$\sqrt{n}$时候的复杂度$O(n^2)$
| inline void init_blk(){
blk=pow(n,1.0/3.0);
rep(i,1,blk) st[i]=n/blk*(i-1)+1,en[i]=n/blk*i;
en[blk]=n;
rep(i,1,blk)
rep(j,st[i],en[i])
bel[j]=i;
}
|
对于询问操作,和普通莫队没有区别,但对于带有时间戳的修改操作,我们需要将这一次查询操作的时间戳和当前的时间戳作比较,如果当前时间戳早了,那么就要一直执行这次查询操作之前的修改操作直到达到这一次操作的时间戳,然后记录答案;如果当前时间戳晚了,那么就要一直撤销修改操作直到到达这一次操作的时间戳,而对于执行和撤销的操作,有一个很聪明的方法:直接swap,因为如果我们这一次查询操作用到了很多次修改,那么如果下一次查询没有用到修改,我们就是把原来的值交换回来,因为时间永远是连续变化的,不可能存在时间间隔几个时间点跳跃的现象
至此,带修改(单点修改)的莫队的原理就结束了(区间修改的莫队似乎还不存在)
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
|
int n,m,st[maxn],en[maxn],blk,bel[maxn],cnt[maxn*8],a[maxn];
int qcnt,mcnt;
int l,r,tim,ans,Ans[maxn];
struct que
{
int l,r,id,tim;
}q[maxn];
struct modi
{
int pos,val;
}md[maxn];
bool cmp(que x1,que x2){
if(bel[x1.l]==bel[x2.l]&&bel[x1.r]==bel[x2.r]) return x1.tim<x2.tim;
if(bel[x1.l]==bel[x2.l]) return bel[x1.r]<bel[x2.r];
return bel[x1.l]<bel[x2.l];
}
inline void init_blk(){
blk=pow(n,1.0/3.0);
rep(i,1,blk) st[i]=n/blk*(i-1)+1,en[i]=n/blk*i;
en[blk]=n;
rep(i,1,blk)
rep(j,st[i],en[i])
bel[j]=i;
}
inline void add(int pos){
if(!cnt[a[pos]]) ++ans;
++cnt[a[pos]];
}
inline void del(int pos){
--cnt[a[pos]];
if(!cnt[a[pos]]) --ans;
}
int main(){
n=read(),m=read();
rep(i,1,n) a[i]=read();
init_blk();
rep(i,1,m){
char c[2];
int l,r;
scanf("%s",c);
l=read(),r=read();
if(c[0]=='Q'){
q[++qcnt].l=l;
q[qcnt].r=r;
q[qcnt].id=qcnt;
q[qcnt].tim=mcnt;
}else{
md[++mcnt].pos=l;
md[mcnt].val=r;
}
}
sort(q+1,q+1+qcnt,cmp);
rep(i,1,m){
int tl=q[i].l,tr=q[i].r,tt=q[i].tim;
while(l<tl) del(l++);
while(l>tl) add(--l);
while(r<tr) add(++r);
while(r>tr) del(r--);
while(tt>tim){
++tim;
if(md[tim].pos>=tl&&md[tim].pos<=tr){
if(!cnt[md[tim].val]) ans++;
++cnt[md[tim].val];
--cnt[a[md[tim].pos]];
if(!cnt[a[md[tim].pos]]) ans--;
}
swap(a[md[tim].pos],md[tim].val);
}
while(tt<tim){
if(md[tim].pos>=tl&&md[tim].pos<=tr){
if(!cnt[md[tim].val]) ans++;
++cnt[md[tim].val];
--cnt[a[md[tim].pos]];
if(!cnt[a[md[tim].pos]]) ans--;
}
swap(a[md[tim].pos],md[tim].val);
--tim;
}
Ans[q[i].id]=ans;
}
rep(i,1,qcnt) write(Ans[i]),putchar('\n');
return 0;
}
|
树上莫队


