线段树专题

浅析：线段树（Segment Tree）

  • 可能我终于算是算法入门了，终于学到了线段树了，加油加油

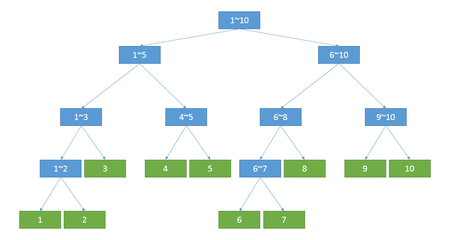
线段树简介

说到线段树嘛，他就是形如下面这样的一颗二叉树，它一般用来维护对于一个序列的各种操作（比如让区间每个数加上一个数 等等）其中每个节点可以维护一段区间的某些值（比如最值、区间和、区间乘积、异或和 等等满足结合律的操作。。。），而每个叶子节点都是一个长度为1的区间，也就代表了序列本身对应下标的值

image.png

线段树操作的复杂度：

建树：$O(nlogn)$

一次区间操作：通常为$O(logn)$

常规线段树

参考blog：

建树

对于一般的线段树，我通常会开一个结构体来存储树的各种信息

注意事项：

  • i<<1和1<<1|1分别表示左儿子和右儿子，位运算能够加快速度，真香

  • 对于区间加减之类的操作（其实乘除、开根号也要），我们都需要一个懒惰标记（lazy tag），这个稍后解释

  • 需要开4倍空间，因为线段树不是一个满二叉树，但我们需要把它开满，防止溢出
1
2
3
struct Stree{
    int l,r,sum,lz;//lz为懒惰标记
}tr[N<<2];//

那么开始建树

1
2
3
4
5
6
7
8
9
10
11
12
inline void build(int i,int l,int r){
    tr[i].l=l,tr[i].r=r,tr[i].lz=0;//加法的懒惰标记初始化为0
    if(l==r){//如果递归到了叶子节点
        tr[i].sum=a[l];
        return;
    }
    int mid=(l+r)>>1;
    build(i<<1,l,mid);//递归建左子树
    build(i<<1|1,mid+1,r);//递归建右子树
    tr[i].sum=tr[i<<1].sum+tr[i<<1|1].sum;//从叶子往根部更新区间和
    return;
}

单点修改

是树状数组不香了吗？

这个就很简单了，直接像二分一样去找到这个下标所在的节点就好啦！

1
2
3
4
5
6
7
8
9
10
inline void modify(int i,int k,int x){//下标位k的数+x
    if(tr[i].l==tr[i].r){
        tr[i].sum+=x;
        return;
    }
    if(tr[i<<1].r>=k) modify(i<<1,k,x);//往哪跑？
    else modify(i<<1|1,k,x);
    tr[i].sum=tr[i<<1].sum+tr[i<<1|1].sum;//记得改完了要更新
    return;
}

区间加法（减法）

对于一个序列，我们需要让[l,r]区间内所有数+k，那么怎么操作呢？

显然如果我们执行（r-l+1）次单点修改的话，时间绝对会炸，因此我们需要更聪明的办法，这个办法就是之前提到的懒惰标记

当我们需要给一个区间的数都加上k时，如果线段树的当前节点包含在这个区间里面，那么我们肯定是要先把这个节点维护的区间和加上（区间长度）*k的值，这是毫无疑问的，但他的儿子区间都要改啊，这太麻烦了，反正现在也不用求答案，倒不如先不对这个区间的儿子进行操作了，先给它打上一个“+k”的标记，我们之后要是要求求和再把这个标记下放到儿子们的区间，那时候再操作也不迟~

这个方法好聪明啊！因此我们在区间修改和查询的时候都需要把懒惰标记下放，同时要让父亲的懒惰标记清零

1
2
3
4
5
6
7
8
9
10
11
12
inline void add(int i,int l,int r,int k){
    if(tr[i].l>=l&&tr[i].r<=r){
        tr[i].sum+=(tr[i].r-tr[i].l+1)*k;//区间和需要对应加上k*(区间长度)
        tr[i].lz+=k;//懒惰标记也要加k
        return;
    }
    push_down(i); //核心：下放操作
    if(tr[i<<1].r>=l) add(i<<1,l,r,k);
    if(tr[i<<1|1].l<=r) add(i<<1|1,l,r,k);
    tr[i].sum=tr[i<<1].sum+tr[i<<1|1].sum;//维护区间和
    return;
}

那么这个下放操作怎么写呢？

对于最简单的区间加法，下放操作就是把加法标记下放给他儿子，同时更新它儿子所维护的区间和就行了

1
2
3
4
5
6
7
8
9
inline void push_down(int i){
    if(tr[i].lz==0) return;
    tr[i<<1].lz+=tr[i].lz;
    tr[i<<1|1].lz+=tr[i].lz;
    tr[i<<1].sum+=(tr[i<<1].r-tr[i<<1|1].l+1)*tr[i].lz;
    tr[i<<1|1].sum+=(tr[i<<1].r-tr[i<<1|1].l+1)*tr[i].lz;
    tr[i].lz=0;//这一步别忘了，不然会死的很惨
    return;
}

询问区间和

对于询问区间和操作，其实就很简单了，如果线段树当前节点对应区间被包含在了询问的区间里，那么直接返回该节点对应的sum即可，否则，就递归地去找左子树和右子树，更新答案（对了，别忘记下放标记，因为这个标记很懒，你不手动下放他是不会动的，哈哈哈~）

1
2
3
4
5
6
7
8
inline ll getsum(int i,int l,int r){
    if(tr[i].l>=l&&tr[i].r<=r) return tr[i].sum;
    push_down(i);//切记！！！
    ll res=0;
    if(tr[i<<1].r>=l) res+=getsum(i<<1,l,r);
    if(tr[i<<1|1].l<=r) res+=getsum(i<<1|1,l,r);
    return res;
}

维护区间最值

对于这个操作，我们可以像维护区间和一样维护，而修改和下放操作也需要加上对应的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
inline void build(int i,int l,int r){//建树时需要维护
    ...
    tr[i].mx=max(tr[i<<1].mx,tr[i<<1|1].mx);
    tr[i].mn=min(tr[i<<1].mn,tr[i<<1|1].mn);
    return;
}
//各种修改的时候也需要维护
inline void push_down(int i){//下放时需要维护
    ...
    tr[i<<1].mx+=tr[i].lz;
    tr[i<<1|1].mx+=tr[i].lz;
    tr[i<<1].mn+=tr[i].lz;
    tr[i<<1|1].mn+=tr[i].lz;
    ...
}

区间乘法+加法（减法）

模板题 线段树2

单独一个区间乘法就很简单了，只需要把上面的懒惰标记改成乘，加号都改为乘号就行了，十分简单，但是如果是乘法和加法同时出现的话，就没这么简单了

因为，我们需要考虑到，对于懒惰标记的操作，到底是先乘再加 还是 先加再乘？

事实表明，先乘再加是最好的解法，我们需要维护两个标记（加法标记and乘法标记），在下放标记的时候，只需要将乘法标记直接下放，而加法标记需要先乘以乘法标记再加上下放的加法标记，然后更新一下儿子们维护的区间和（同上）就行了

下放操作：

1
2
3
4
5
6
7
8
9
10
11
12
inline void push_down(int i){//区间加乘的下放操作
    int k1=tr[i].plz,k2=tr[i].mlz;//plz:加法标记，mlz:乘法标记
    tr[i<<1].sum=(tr[i<<1].sum*k2+k1*(tr[i<<1].r-tr[i<<1].l+1))%p;
    tr[i<<1|1].sum=(tr[i<<1].sum*k2+k1*(tr[i<<1|1].r-tr[i<<1|1].l+1))%p;//先乘再加
    tr[i<<1].plz=(tr[i<<1].plz*k2+k1)%p;
    tr[i<<1|1].plz=(tr[i<<1|1].plz*k2+k1)%p;
    tr[i<<1].mlz=(tr[i<<1].mlz*k2)%p;
    tr[i<<1|1].mlz=(tr[i<<1|1].mlz*k2)%p;
    tr[i].mlz=1;//乘法标记初始化一定是1
    tr[i].plz=0;
    return;
}

对于区间修改操作，区间加法我们可以无脑直接加，而区间乘法则需要同时把加法标记乘以这个数k

修改操作：（[l,r]内每个数加上、乘以k）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
inline void add(int i,int l,int r,int k){//区间加法
    if(tr[i].l>=l&&tr[i].r<=r){
        tr[i].sum=(tr[i].sum+k*(tr[i].r-tr[i].l+1))%p;
        tr[i].plz=(tr[i].plz+k)%p;
        return;
    }
    ...
}
inline void mul(int i,int l,int r,int k){//区间乘法
    if(tr[i].l>=l&&tr[i].r<=r){
        tr[i].sum=(tr[i].sum*k)%p;
        tr[i].plz=(tr[i].plz*k)%p;//加法标记一定要要对应*k
        tr[i].mlz=(tr[i].mlz*k)%p;
        return;
    }
    ...
}

区间除法&区间开根号

区间开根号模板题：花神游历各国

对于这两种操作，显然他们不满足结合律，但是，这样我们就不能线段树了吗？

大错特错！我们来考虑除法与开根号这些运算的特性：他们都会使得一堆元素（整数）不断地减小，并且趋于一个值（除法趋于0，开根号趋于1）

针对除法来说：对于一个区间的所有元素而言，如果这个区间内元素最大值与他除以除数所得商的差值 等于 最小值与他除以除数所得商的差值，那么这个区间内的所有元素除以除数都会减去同一个数，于是就可以给这个区间的加法标记做一点操作，就可以把区间除法转换成区间减法啦！

同理，如果这个区间的最大值与它开根号的差值 等于 最小值与它开根号的差值，那么这个区间内的所有元素开根号都会减去同一个数，我们就能把开根号转换为减法啦！

所以说，对于区间除法和区间开根号操作，他们都可以转化为区间减法操作来优化复杂度（这十分重要，否则就是一个单纯的暴力了呀~）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
inline void Sqrt(int i,int l,int r){//区间开根号
    if(tr[i].l>=l&&tr[i].r<=r){
        int k1=tr[i].mx-floor(sqrt(tr[i].mx));//核心，转换为减法
        int k2=tr[i].mn-floor(sqrt(tr[i].mn));
        if(k1==k2){//判断是否可以对整个区间操作
            tr[i].lz-=k1;
            tr[i].sum-=k1*(tr[i].r-tr[i].l+1);
            tr[i].mx-=k1;
            tr[i].mn-=k1;
            return;//这个return要写在里面
        }
    }
	...
}
inline void div(int i,int l,int r,int k){//区间除法
    ...
    if(tr[i].l>=l&&tr[i].r<=r){
        int k1=tr[i].mx-tr[i].mx/k;//核心
        int k2=tr[i].mn-tr[i].mn/k;
        if(k1==k2){
            tr[i].sum-=k1*(tr[i].r-tr[i].l+1);
            tr[i].lz-=k1;
            tr[i].mx-=k1;
            tr[i].mn-=k1;
        }
    }
    ...//其他都一样
}

然而，对于区间开根号操作，还有更好的办法：对于一个很大的数，我们只要不断对其开根号，用不了几次它就会变成1，那么我们可以通过维护区间最大值是否小于等于1来判断这个区间是否有必要操作，这样就可以大大优化时间复杂度

1
2
3
4
5
6
7
8
9
10
11
12
inline void Sqrt(int i,int l,int r){
    if(tr[i].l==tr[i].r){
        tr[i].sum=tr[i].mx=sqrt(tr[i].sum);
        return;
    }
    push_down(i);
    //判断是否有必要对这个区间开根号
    if(tr[i<<1].r>=l&&tr[i<<1].mx>1) Sqrt(i<<1,l,r);
    if(tr[i<<1|1].l<=r&&tr[i<<1|].mx>1) Sqrt(i<<1|1,l,r);
    tr[i].sum=tr[i<<1].sum+tr[i<<1|1].sum;
    tr[i].mx=max(tr[i<<1].mx,tr[i<<1|1].mx);
}

UPD 2020.6.8

这几天学校训练做了一道类似的题USST训练赛9 时间管理，题意大概是区间gcd修改+区间求和，对于区间gcd，可以同样用线段数（或分块）维护区间的值是否相同，若相同，直接$O(1)$修改该区间和即可，因为gcd操作和开根号操作一样，总是让一段区间趋于1的

线段树 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
ll a[maxn],n,m;
/* Normal Segment Tree */
struct SegmentTree
{	
	#define ls i<<1
	#define rs i<<1|1
	struct Tree{
		int l,r;
		ll sum,ptg,minh,maxh;
	}tr[maxn<<2];

	inline void push_up(int i){
		tr[i].sum=tr[ls].sum+tr[rs].sum;
		tr[i].minh=min(tr[ls].minh,tr[rs].minh);
		tr[i].maxh=max(tr[ls].maxh,tr[rs].maxh);
	}

	inline void push_down(int i){
		if(tr[i].ptg==0) return;
		ll k=tr[i].ptg;
		tr[ls].sum+=k*(tr[ls].r-tr[ls].l+1);
		tr[rs].sum+=k*(tr[rs].r-tr[rs].l+1);
		tr[ls].minh+=k;
		tr[ls].maxh+=k;
		tr[rs].minh+=k;
		tr[rs].maxh+=k;
		tr[ls].ptg+=k;
		tr[rs].ptg+=k;
		tr[i].ptg=0;
	}

	inline void build(int i,int l,int r){
		tr[i].l=l,tr[i].r=r;
		tr[i].ptg=0;
		if(tr[i].l==tr[i].r){
			tr[i].sum=a[l];
			tr[i].minh=a[l];
			tr[i].maxh=a[l];
			return;
		}
		int mid=(l+r)>>1;
		build(ls,l,mid);
		build(rs,mid+1,r);
		push_up(i);
	}

	inline void change(int i,int l,int r,ll k){
		if(tr[i].l>=l&&tr[i].r<=r){
			if(tr[i].minh==tr[i].maxh){
				ll tp=gcd(tr[i].minh,k)-tr[i].minh;
				tr[i].sum+=tp*(tr[i].r-tr[i].l+1);
				tr[i].ptg+=tp;
				tr[i].minh+=tp;
				tr[i].maxh+=tp;
				return;
			}
		}
		push_down(i);
		if(tr[ls].r>=l) change(ls,l,r,k);
		if(tr[rs].l<=r) change(rs,l,r,k);
		push_up(i);
	}

	inline ll getsum(int i,int l,int r){
		if(tr[i].l>=l&&tr[i].r<=r)
			return tr[i].sum;
		push_down(i);
		ll res=0;
		if(tr[ls].r>=l) res+=getsum(ls,l,r);
		if(tr[rs].l<=r) res+=getsum(rs,l,r);
		return res;
	}
}T;

int main(){
	read(n),read(m);
	rep(i,1,n) read(a[i]);
	T.build(1,1,n);
	int op,l,r,x;
	rep(i,1,m){
		read(op),read(l),read(r);
		if(op&1){
			read(x);
			T.change(1,l,r,x);
		}else{
			printf("%lld\n",T.getsum(1,l,r));
		}
	}
	return 0;
}
分块 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121

ll a[maxn],n,m,blk,bel[maxn],sz[maxn],st[maxn],en[maxn],tg[maxn];
ll minh[maxn],maxh[maxn];
ll sum[maxn];
inline void init_blk(){
	blk=sqrt(n);
	rep(i,1,blk){
		st[i]=n/blk*(i-1)+1;
		en[i]=n/blk*i;
		minh[i]=inf;
		maxh[i]=-inf;
	}
	en[blk]=n;
	rep(i,1,blk){
		sz[i]=en[i]-st[i]+1;
		rep(j,st[i],en[i]){
			bel[j]=i;
			minh[i]=min(minh[i],a[j]);
			maxh[i]=max(maxh[i],a[j]);
		}
	}
}

inline void change(ll l,ll r,ll x){
	if(bel[l]==bel[r]){
		for(int i=l;i<=r;i++){
			a[i]=gcd(a[i]+tg[bel[l]],x);
		}
		minh[bel[l]]=inf,maxh[bel[l]]=-inf;
		for(int i=st[bel[l]];i<=en[bel[l]];i++){
			if(i<l||i>r) a[i]+=tg[bel[l]];
			minh[bel[l]]=min(minh[bel[l]],a[i]),
			maxh[bel[l]]=max(maxh[bel[l]],a[i]);
		}
		tg[bel[l]]=0;
	}else{
		// left blk
		for(int i=l;i<=en[bel[l]];i++){
			a[i]=gcd(a[i]+tg[bel[l]],x);
		}
		minh[bel[l]]=inf,maxh[bel[l]]=-inf;
		for(int i=st[bel[l]];i<=en[bel[l]];i++){
			if(i<l) a[i]+=tg[bel[l]];
			minh[bel[l]]=min(minh[bel[l]],a[i]),
			maxh[bel[l]]=max(maxh[bel[l]],a[i]);
		}
		tg[bel[l]]=0;
		// right blk
		for(int i=st[bel[r]];i<=r;i++){
			a[i]=gcd(a[i]+tg[bel[r]],x);
		}
		minh[bel[r]]=inf,maxh[bel[r]]=-inf;
		for(int i=st[bel[r]];i<=en[bel[r]];i++){
			if(i>r) a[i]+=tg[bel[r]];
			minh[bel[r]]=min(minh[bel[r]],a[i]),
			maxh[bel[r]]=max(maxh[bel[r]],a[i]);
		}
		tg[bel[r]]=0;
		// middle whole blk
		for(int i=bel[l]+1;i<=bel[r]-1;i++){
			if(minh[i]==maxh[i]){
				int tp=gcd(minh[i],x);
				tg[i]+=tp-minh[i];
				minh[i]=maxh[i]=tp;
			}else{
				for(int j=st[i];j<=en[i];j++){
					a[j]=gcd(a[j]+tg[i],x);
				}
				minh[i]=inf,maxh[i]=-inf;
				for(int j=st[i];j<=en[i];j++){
					minh[i]=min(minh[i],a[j]),
					maxh[i]=max(maxh[i],a[j]);
				}
				tg[i]=0;
			}
		}
	}
}

inline ll getsum(ll l,ll r){
	ll res=0;
	if(bel[l]==bel[r]){
		for(int i=l;i<=r;i++){
			res+=(a[i]+tg[bel[l]]);
		}
	}else{
		for(int i=l;i<=en[bel[l]];i++){
			res+=(a[i]+tg[bel[l]]);
		}
		for(int i=st[bel[r]];i<=r;i++){
			res+=(a[i]+tg[bel[r]]);
		}
		for(int i=bel[l]+1;i<=bel[r]-1;i++){
			if(minh[i]==maxh[i]){
				res+=(sz[i]*minh[i]);
			}else{
				for(int j=st[i];j<=en[i];j++){
					res+=(a[j]+tg[i]);
				}
			}
		}
	}
	return res;
}

int main(){
	read(n),read(m);
	rep(i,1,n) read(a[i]);
	init_blk();
	int op,l,r,x;
	rep(i,1,m){
		read(op),read(l),read(r);
		if(op&1){
			read(x);
			change(l,r,x);
		}else{
			printf("%lld\n",getsum(l,r));
		}
	}
	return 0;
}

Lazy Tag的用途

来源于这道典型例题：Mayor’s posters（线段树+离散化）

就像铺地毯一样，我们不停地在某些区间上铺一些地毯，最后问能在整个区间看到多少种颜色的地毯？

这题我们离线做（动态开点目前没学orz），首先离散化三部曲（排序 去重 二分插入，否则你会MLE）我就不多说了，那么这个题怎么用Lzay Tag来维护呢，我们很容易想到整个区间的种类数比较好求，只要开一个vis数组记录就行了，而这个离线的区间更新怎么做呢？我们思考区间求和的懒惰标记是维护的求和的加数，但是我们这是维护一个颜色（即种类），如果一个区间的子区间的颜色在后来被修改了，那么我们就需要把这个区间的lazytag下放，直到给到那个被修改的子区间，然后把那个修改的子区间的颜色改成要修改成的颜色，这样一来，维护了这个区间其他子区间颜色没变，而只改变了这一个区间的颜色，非常巧妙

code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
ll t,n,tot,l,r,vis[N],b[N];
struct node{
	ll l,r;
}a[N];
struct Stree{
	ll l,r,col;
}tree[N<<2];
inline void init(){
	memset(b,0,sizeof(b));
	memset(vis,0,sizeof(vis));
	ll temp=0;
	scanf("%lld",&n);
	for(int i=1;i<=n;i++){
		scanf("%lld%lld",&a[i].l,&a[i].r);
		b[++temp]=a[i].l,b[++temp]=a[i].r;
	}
	sort(b+1,b+1+temp);
	tot=unique(b+1,b+1+temp)-b-1;
	for(int i=1;i<=n;i++){
		a[i].l=lower_bound(b+1,b+1+tot,a[i].l)-b;
		a[i].r=lower_bound(b+1,b+1+tot,a[i].r)-b;
	}
}
inline void build(ll i,ll l,ll r){
	tree[i].l=l,tree[i].r=r,tree[i].col=0;
	if(l==r){
		return;
	}
	ll mid=(l+r)>>1;
	build(i<<1,l,mid);
	build(i<<1|1,mid+1,r);
	return;
}
inline void push_down(ll i){
	if(tree[i].col==0) return;
	tree[i<<1].col=tree[i<<1|1].col=tree[i].col;
	tree[i].col=0;
	return;
}
inline void update(ll i,ll l,ll r,ll col){
	if(tree[i].l>=l&&tree[i].r<=r){
		tree[i].col=col;
		return;
	}
	push_down(i);
	if(tree[i<<1].r>=l) update(i<<1,l,r,col);
	if(tree[i<<1|1].l<=r) update(i<<1|1,l,r,col);
}
inline void search(ll i,ll l,ll r,ll &ans){
	if(tree[i].col){
		if(!vis[tree[i].col]){
			vis[tree[i].col]=1;
			ans++;
		}
		return;
	}
	search(i<<1,l,r,ans);
	search(i<<1|1,l,r,ans);
	return;
}
inline ll ask(ll l,ll r){
	ll ans=0;
	search(1,l,r,ans);
	return ans;
}

int main() {
    scanf("%lld",&t);
    while(t--){
    	init();
	    build(1,1,tot);
	    ll col=0;
	    for(int i=1;i<=n;i++){
	    	update(1,a[i].l,a[i].r,++col);
		}
		printf("%lld\n",ask(1,tot));
	}
    return 0;
}

权值线段树

例题：洛谷 P1801 黑匣子（离散化+权值线段树）

与一般的线段树有一点区别：权值线段树的每个叶子节点就代表了数列中一个具体的值（我们称之为权值），而每个叶子节点维护的是这个具体的值在整个数列中出现的次数，每一个父亲节点维护了一段区间的值出现的总次数，这样一来，权值线段树的意义就很明朗了

权值线段树的一个重要应用：求整个数列中第k大（第k小）的数（注意是整个数列）

算法：权值线段树的基本操作和普通线段树几乎相同，需要注意的是以下几点：

  • 每个节点维护的不再是权值or区间和，而是该节点代表数字出现的次数

    比如我们可以开一个结构体存储

    1
    2
    3
    4
    struct Stree{
        int l,r;//维护该子树对应的左右区间端点
        int v;//维护数的出现次数
    }tr[N<<2];//照样开4倍大

  • 更新操作（比如插入了一个数），就是递归找到该数对应的叶子节点，给节点维护的次数+1

  • 询问操作（以询问第k小为例），递归地找，如果左子树内有大于等于k个数字，那么就递归进入左子树找第k小，否则就递归进入右子树找第k-tr[rs].v小

例题代码：

code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<bits/stdc++.h>
using namespace std;
#define ls (i<<1)
#define rs (i<<1|1)
const int N=2e5+5;
int n,m,b[N],c[N],cnt=1;
struct node{
	int val,id;
}a[N];
bool cmp(node x1,node x2){
	return x1.val<x2.val;
}
struct Stree{
	int l,r,v;
}tr[N<<2];
inline void build(int i,int l,int r){//建树
	tr[i].l=l,tr[i].r=r;
	if(l==r) return;
	int mid=(l+r)>>1;
	build(ls,l,mid);
	build(rs,mid+1,r);
}
inline void update(int i,int x){//插入并更新
	if(tr[i].l==tr[i].r){
		tr[i].v++;//次数+1
		return;
	}
	if(tr[ls].r>=x) update(ls,x);//找到位置
	else update(rs,x);
	tr[i].v=tr[ls].v+tr[rs].v;//push_up
}
inline int getval(int i,int k){//获得对应权值
	if(tr[i].l==tr[i].r){
		return tr[i].l;
	}
	if(tr[ls].v>=k) return getval(ls,k);
	else return getval(rs,k-tr[ls].v);
}
int main() {
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&a[i].val),a[i].id=i;
    sort(a+1,a+1+n,cmp);//离散化排序
    for(int i=1;i<=n;i++) c[a[i].id]=i;//找出每个点的相对大小位置
    for(int i=1;i<=m;i++) scanf("%d",&b[i]);
    build(1,1,n);
    for(int i=1;i<=n;i++){
    	update(1,c[i]);//插入操作
    	while(b[cnt]==i){
    		printf("%d\n",a[getval(1,cnt)].val); 
    		cnt++;
		}
	}
    return 0;
}

动态开点线段树

参考blog：

这东西就比较神了，它是线段树的（阉割）简化版，原理就是：我们不会在询问出现之前就利用build函数建立一颗完整的满二叉树结构的线段树（因为这样可能会有很多节点的空间没有用上，浪费了空间），而是采用边询问边建树的方式动态开点，这样以来，不用的节点我们不开，用的节点我们用的时候再开，可以很高效地处理值域较大（1e9），但是操作次数较少（1e5）的操作，或是需要建立多棵独立的线段树的时候

通常情况下，我们为动态开点线段树开（修改次数*40）的空间（类似主席树），然后根据RE和MLE来修改空间，其余特征和普通线段树无差异（pushdown下放，pushup更新）

注意事项：

  • 我们不再开结构体（可以但没必要）存树，因为它不再满足儿子节点为根节点编号的两倍和两倍加一原则（不是满二叉树），而是利用一个时间戳编号来存储节点编号
  • 也不需要存储每个节点所对应的区间左右端点值（其实普通线段树也没必要存）
1
2
3
4
const int N=1e5+5;
int ls[N*40],rs[N*40],tg[N*40],rt,ncnt;
ll sum[N*40];
//rt为根节点编号，ncnt为节点数（时间戳），动态开点时用到

下面放线段树1的动态开点形式：

code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int n,m,op,x,y,k,ls[N*40],rs[N*40],tg[N*40],rt,ncnt;
ll sum[N*40];

inline void pushup(int o){
	sum[o]=sum[ls[o]]+sum[rs[o]];
}

inline void init(int &o,int l,int r,int x,int k){
	if(!o) o=++ncnt;
	if(l==r){
		sum[o]+=1ll*k;
		return;
	}
	int mid=(l+r)>>1;
	if(mid>=x) init(ls[o],l,mid,x,k);
	else init(rs[o],mid+1,r,x,k);
	pushup(o);
}

inline void push_down(int o,int l,int r){
	if(!tg[o]) return;
	if(!ls[o]) ls[o]=++ncnt;
	if(!rs[o]) rs[o]=++ncnt;
	int mid=(l+r)>>1;
	sum[ls[o]]+=tg[o]*(mid-l+1);
	sum[rs[o]]+=tg[o]*(r-mid);
	tg[ls[o]]+=tg[o];
	tg[rs[o]]+=tg[o];
	tg[o]=0;
	return;
}

inline void update(int &o,int l,int r,int L,int R,int k){
	if(!o) o=++ncnt;
	if(l>=L&&r<=R){
		sum[o]+=1ll*k*(r-l+1);
		tg[o]+=k;
		return;
	}
	push_down(o,l,r);
	int mid=(l+r)>>1;
	if(mid>=L) update(ls[o],l,mid,L,R,k);
	if(mid+1<=R) update(rs[o],mid+1,r,L,R,k);
	pushup(o);
}

inline ll getsum(int &o,int l,int r,int L,int R){
	if(!o) return 0;
	if(l>=L&&r<=R) return sum[o];
	push_down(o,l,r);
	ll res=0;
	int mid=(l+r)>>1;
	if(mid>=L) res+=getsum(ls[o],l,mid,L,R);
	if(mid+1<=R) res+=getsum(rs[o],mid+1,r,L,R);
	return res;
}

int main() {
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
    	scanf("%d",&x);
    	init(rt,1,n,i,x);
	}
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&op,&x,&y);
		if(op==1){
			scanf("%d",&k);
			update(rt,1,n,x,y,k);
		}else{
			printf("%lld\n",getsum(rt,1,n,x,y));
		}
	}
    return 0;
}

可持久化线段树（主席树）

题目链接：P3834 【模板】可持久化线段树 1（主席树）

参考blog：

题意：给定$n$个整数构成的序列，将对于指定的闭区间查询其区间内的第$k$小值

经典得不能再经典的区间$Kth$问题，即（强制在线的）询问若干区间内的 $k$大/$k$小 值，对于这类问题，当然可以使用暴力$O(nq)$，但是你会T得很惨，于是便又出现了一种神仙数据结构——可持久化线段树（或 主席树，据说是因为发明人的名字缩写叫hjt）

其实主席树并不是什么新的数据结构，本质上它其实是权值线段树+前缀和思想应用的结合，原理描述起来也十分简单，即：开$n$棵权值线段树，第$i$棵维护序列的前$i$个数的出现次数，对于每一次$[l,r]$的询问，用第$r$棵线段树减去第$l-1$棵线段树，得出的新线段树就是维护了$[l,r]$区间的每个数的出现次数的权值线段树，然后在这棵树上二分求解$Kth$就行了，但是，仅仅这样做会使得空间特别大导致RE，因此需要优化，优化过后的这些树就是主席树啦，那么如何进行空间优化呢？

我们发现，对于每一次插入新的序列中的值时，都构建出一颗完整的权值线段树是不值得的，因为有很多的点早就已经在之前构建的权值线段树中出现过了，且没有发生改变，这些点没必要再重新新建，直接利用之前构建好的点就行了，因此，单次的更新只需要新建$log(n)$个新节点即可，空间大大缩减

举个栗子：4 3 2 3 6 1

初始时，只有一棵空的线段树，所有节点对应的出现次数为0，当加入区间$[1,1]$时，即 将4的出现次数+1，此时，只需要将与4节点有关的节点维护的次数值+1即可，剩余的节点不需要改变，直接连回去即可

在这里插入图片描述

插入$[1,3]$区间后得到的线段树如下图所示：

在这里插入图片描述

  • 时间复杂度：建树$O(nlogn)$，单次询问$O(logn)$

  • 空间复杂度：通常情况$O(nlog^2n)$

接下来是代码实现

一些变量

T[maxn*50]：存储每棵线段树的根节点

ls[maxn*50]：存储左儿子编号

rs[maxn*50]：存储右儿子编号

ci[maxn*50]：记录节点对应权值（出现次数）

tcnt：节点个数

离散化

通常情况下，如果要求$Kth$，给出的数值一般都比$n$大很多，所以需要离散化，否者会炸空间RE哦

1
2
3
rep(i,1,n) read(a[i]),b[i]=a[i];
sort(b+1,b+1+n);
int len=unique(b+1,b+1+n)-b-1;

Build建树函数

1
2
3
4
5
6
7
void build(int &rt,int l,int r){
    rt=++tcnt,ci[rt]=0;
    if(l==r) return;
    int mid=(l+r)>>1;
    build(ls[rt],1,mid);
    build(rs[rt],mid+1,r);
}

Update更新函数

1
2
3
4
5
6
7
8
9
10
int update(int o,int l,int r,int val){
    int oo=++tcnt;
    //新节点的左右儿子与原节点相同
    ls[oo]=ls[o],rs[oo]=rs[o],ci[oo]=ci[o]+1;//在之前的节点基础上+1
    if(l==r) return oo;//如果到叶子了，返回新节点标号
    int mid=(l+r)>>1;
    if(mid>=val) ls[oo]=update(ls[oo],l,mid,val);//递归求左右节点新标号
    else rs[oo]=update(rs[oo],mid+1,r);
    return oo;//返回新节点序号
}

Query询问函数

1
2
3
4
5
6
7
int query(int L,int R,int l,int r,int k){
    int mid=(l+r)>>1;
    int x=ci[ls[R]]-ci[ls[L]];//x为区间[l,r]中数的出现次数之和
    if(l==r) return l;
    if(x>=k) return query(ls[L],ls[R],l,mid,k);
    else return query(rs[L],rs[R],mid+1,r,k-x);
}

完整模板题代码

通常情况下，主席树的空间需要开32~50倍的序列长度大小，总之，能开多大开多大吧

code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(register int i=a;i<=b;i++)
#define All(x) (x).begin(),(x).end()
#define pb push_back
#define mp make_pair
typedef long long ll;
typedef double db;
typedef vector<int> VI;
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const double eps=1e-6;
const long long mod=1e9+7;
const int inf=0x7fffffff;
const int maxn=200005;
ll qpow(ll x,ll y,ll Mod) {ll ans=1,base=x%Mod; while(y){if(y&1)ans=(ans*base)%Mod;base=(base*base)%Mod;y>>=1;} return ans;}
ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}

// fast read
template<class T> void read(T &x) {
	x=0;int f=0;char ch=getchar();
	while(ch<'0'||ch>'9'){f|=(ch=='-');ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	x=f?-x:x;
	return;
}

int n,m,type,a[maxn],b[maxn],ans;
int T[maxn*40],ls[maxn*40],rs[maxn*40],ci[maxn*40],tcnt;

inline void build(int &rt,int l,int r){
	rt=++tcnt,ci[rt]=0;
	if(l==r) return;
	int mid=(l+r)>>1;
	build(ls[rt],l,mid);
	build(rs[rt],mid+1,r);
}

int update(int ort,int l,int r,int val){
	int nrt=++tcnt;
	ls[nrt]=ls[ort],rs[nrt]=rs[ort],ci[nrt]=ci[ort]+1;
	if(l==r) return nrt;
	int mid=(l+r)>>1;
	if(mid>=val) ls[nrt]=update(ls[nrt],l,mid,val);
	else rs[nrt]=update(rs[nrt],mid+1,r,val);
	return nrt;
}

int query(int lt,int rt,int l,int r,int k){
	if(l==r) return l;
	int mid=(l+r)>>1,x=ci[ls[rt]]-ci[ls[lt]];
	if(x>=k) return query(ls[lt],ls[rt],l,mid,k);
	else return query(rs[lt],rs[rt],mid+1,r,k-x);
}

int main(){
	read(n),read(m);
	rep(i,1,n) read(a[i]),b[i]=a[i];
	sort(b+1,b+1+n);
	int len=unique(b+1,b+1+n)-b-1;
	build(T[0],1,len);
	rep(i,1,n){
		int x=lower_bound(b+1,b+1+len,a[i])-b;
		T[i]=update(T[i-1],1,len,x);
	}
	for(int i=0,x,y,k;i<m;i++){
		read(x),read(y),read(k);
		printf("%d\n",b[query(T[x-1],T[y],1,len,k)]);
	}
	return 0;
}

习题

P3834 【模板】可持久化线段树 1（主席树）

P3567 [POI2014]KUR-Couriers（动态询问区间是否存在出现次数大于一半的数）

UPD：2022.10.3

时光荏苒，一转眼两年半过去了，现在再回过头来看之前学习的算法和数据结构，代码风格实在是不敢苟同（我为什么当时能写得出这么OI风格的代码？？）如今加深了对语言和算法的认识，现在重新拾起旧知识的时候，有了很多自己的想法和思考。接下来介绍一下线段树常用小技巧 之 线段树合并。

线段树合并

参考blog：

首先我们先规定一下线段树的节点结构体：存储了需要维护的值val、左儿子下标LS、右儿子下标RS。

这棵树是由一个vector<Node>来维护的。

1
2
3
4
5
6
7
8
9
struct Node {
    T val;
    int LS, RS;
    Node(): val(0) {
        LS = 0, RS = 0;
    }
};

vector<Node> tr;

动态开点线段树合并，简称线段树合并，顾名思义，就是将两棵线段树的节点值合并，注意这里的合并是指维护的信息合并，例如：区间和的合并，就是将两个节点的区间和相加。线段树合并的代码十分简单：

  • 如果两棵树对应节点任意一个没有被开辟，则返回另一个节点
  • 如果是叶子节点，将信息合并
  • 递归左右子树

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 线段树合并：将b为根的树合并到a为根的树上
int merge(int a, int b, int l, int r){
    if(!a) return b;
    if(!b) return a;
    if(l == r){
        /* 合并信息操作 */
        // 例如：tr[a].val += tr[b].val;
        return a;
    }
    int mid = (l + r) >> 1;
    tr[a].LS = merge(tr[a].LS, tr[b].LS, l, mid);
    tr[a].RS = merge(tr[a].RS, tr[b].RS, mid + 1, r);
    push_up(a);
    return a;
}

线段树合并的时间复杂度与树中插入的节点个数有关，如果我们需要加入$k$个点，则会向树中会插入$k \log k$个节点，每次合并两棵线段树同位置的点，就会少掉一个点，这个复杂度是$O(1)$的，因此线段树合并的总复杂度为$O(k\log k)$，具体证明可以参考上方blog。

习题

P3605 USACO17JAN Promotion Counting P

题意：一棵有根树，求每个子树中严格大于当前节点值的节点个数

题解：对每个节点维护一棵动态开点线段树，线段树维护区间和，然后直接dfs + 线段树合并

code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
/*

    https://www.luogu.com.cn/problem/P3605
    线段树合并模板题

    一棵有根树，求每个子树中严格大于当前节点值的节点个数

*/

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int,int>;


#define DYNAMIC // 是否开启动态开点
template<class T>
class SegTree {
public:
    static constexpr T T_MIN = numeric_limits<T>::lowest();
    static constexpr T T_MAX = numeric_limits<T>::max();

    struct Node {
        T val;
        #ifdef DYNAMIC
            int LS, RS;
        #endif
        Node(): val(0) {
            #ifdef DYNAMIC
                LS = 0, RS = 0;
            #endif
        }
    };

    #ifdef DYNAMIC
        #define ls (tr[i].LS)
        #define rs (tr[i].RS)
        int tcnt; // 动态节点数
    #else
        #define ls (i<<1)
        #define rs (i<<1|1)
    #endif

    vector<Node> tr;

    void push_down(int i, int l, int r) {
        #ifdef DYNAMIC
            if(!ls) ls = ++tcnt, tr.emplace_back(Node{});
            if(!rs) rs = ++tcnt, tr.emplace_back(Node{});
        #endif
    }
    void push_up(int i) {
        tr[i].val = tr[ls].val + tr[rs].val;
    }


    /* 构造与初始化 */
    #ifdef DYNAMIC
        SegTree(): tcnt(1), tr(2) {}
        // 开N棵动态开点线段树，根节点分别为 1 ~ N（用于线段树合并）
        SegTree(const int &N): tcnt(N), tr(N+1) {}

        // 线段树合并：将b为根的树合并到a为根的树上
        int merge(int a, int b, int l, int r){
            if(!a) return b;
            if(!b) return a;
            if(l == r){
                /* 合并信息操作 */
                tr[a].val += tr[b].val;
                return a;
            }
            int mid = (l + r) >> 1;
            tr[a].LS = merge(tr[a].LS, tr[b].LS, l, mid);
            tr[a].RS = merge(tr[a].RS, tr[b].RS, mid + 1, r);
            push_up(a);
            return a;
        }
    #else
        // 初值初始化
        void build(int i,int l,int r,const vector<T> &a){
            if(l==r){
                tr[i].val = a[l];
                tr[i].maxh = a[l];
                return;
            }
            int mid = (l + r) >> 1;
            build(ls, l, mid, a);
            build(rs, mid+1, r, a);
            push_up(i);
        }

        void RESIZE(const int &N) { tr.resize(N<<2); }
        SegTree() = default;
        SegTree(const int &N): tr(N<<2) {}
        SegTree(const int &N, const vector<T> &a): tr(N<<2) { build(1, 1, N, a); }
    #endif
    /* 构造与初始化 */


    // 单点修改
    void add_point(int i, int l, int r, int pos, T k) {
        if (l == r) {
            tr[i].val += k;
            return;
        }
        push_down(i, l, r);
        int mid = (l + r) >> 1;
        if (pos <= mid) add_point(ls, l, mid, pos, k);
        else add_point(rs, mid+1, r, pos, k);
        push_up(i);
    }

    // 区间求和
    T getsum(int i, int l, int r, int L, int R) {
        if (l >= L && r <= R) return tr[i].val;
        push_down(i, l, r);
        int mid = (l + r) >> 1;
        T ret = 0;
        if (mid >= L) ret += getsum(ls, l, mid, L, R);
        if (mid+1 <= R) ret += getsum(rs, mid+1, r, L, R);
        return ret;
    }


};
////////////////////////////////////////////////////////

void solve(){
    
    int n;
    cin >> n;
    vector<vector<int>> e(n+1);
    vector<int> a(n+1);
    for(int i=1;i<=n;++i) cin >> a[i];
    for(int fa,i=2;i<=n;++i){
        cin >> fa;
        e[i].emplace_back(fa);
        e[fa].emplace_back(i);
    }
    vector<int> ans(n+1);
    SegTree<int> seg(n);
    auto dfs = [&](auto &&self, int u, int fath) -> void{
        for(auto &&v: e[u]){
            if(v == fath) continue;
            self(self, v, u);
            seg.merge(u, v, 1, 1e9);
        }
        ans[u] = seg.getsum(u, 1, 1e9, a[u]+1, 1e9);
        seg.add_point(u, 1, 1e9, a[u], 1);
    };
    dfs(dfs, 1, -1);
    
    for(int i=1;i<=n;++i) cout << ans[i] << '\n';
    
}

int main(){
    
    cin.tie(nullptr)->sync_with_stdio(false);
    
    int _ = 1;
    // cin>>_;
    while(_--){
        
        solve();
        
    }
    
    return 0;
}

P4556 Vani有约会 雨天的尾巴 /【模板】线段树合并

题意：一棵有根树，m次操作，每次给[x,y]路径上所有点发放z类型的食物，问所有操作后，每个点存放的最多的是哪种食物？

题解：首先，[x,y]路径操作可以转化成树上差分，即x+1, y+1, LCA(x,y)-1, fa[LCA(x,y)]-1。对每个节点维护一棵动态开点线段树，线段树维护该点的每种食物的出现次数 和 出现次数最大的食物下标。先树上差分将所有修改处理好，然后dfs + 线段树合并，注意合并时需要保证合并好所有信息。（易错点：可能会出现每种食物的出现次数=0，但出现次数最大的食物下标≠0的情况，这里需要特判使得ans = 0）

code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int,int>;


#define DYNAMIC // 是否开启动态开点
template<class T>
class SegTree {
public:
    static constexpr T T_MIN = numeric_limits<T>::lowest();
    static constexpr T T_MAX = numeric_limits<T>::max();

    struct Node {
        T maxh, maxidx;
        #ifdef DYNAMIC
            int LS, RS;
        #endif
        Node(): maxh(0), maxidx(0) {
            #ifdef DYNAMIC
                LS = 0, RS = 0;
            #endif
        }
    };

    #ifdef DYNAMIC
        #define ls (tr[i].LS)
        #define rs (tr[i].RS)
        int tcnt; // 动态节点数
    #else
        #define ls (i<<1)
        #define rs (i<<1|1)
    #endif

    vector<Node> tr;

    void push_down(int i, int l, int r) {
        #ifdef DYNAMIC
            if(!ls) ls = ++tcnt, tr.emplace_back(Node{});
            if(!rs) rs = ++tcnt, tr.emplace_back(Node{});
        #endif
    }

    void push_up(int i) {
        if(tr[ls].maxh >= tr[rs].maxh) tr[i].maxh = tr[ls].maxh, tr[i].maxidx = tr[ls].maxidx;
        else tr[i].maxh = tr[rs].maxh, tr[i].maxidx = tr[rs].maxidx;
    }

    /* 构造函数 */
    #ifdef DYNAMIC

        SegTree(): tcnt(1), tr(2) {}
        // 开N棵动态开点线段树，根节点分别为 1 ~ N（一般用于线段树合并）
        SegTree(const int &N): tcnt(N), tr(N+1) {}

        // 线段树合并：将b为根的树合并到a为根的树上
        int merge(int a, int b, int l, int r){
            if(!a) return b;
            if(!b) return a;
            if(l == r){
                tr[a].maxh += tr[b].maxh;
                tr[a].maxidx = l;
                return a;
            }
            int mid = (l + r) >> 1;
            tr[a].LS = merge(tr[a].LS, tr[b].LS, l, mid);
            tr[a].RS = merge(tr[a].RS, tr[b].RS, mid + 1, r);
            push_up(a);
            return a;
        }

    #else

        // 初值初始化
        void build(int i,int l,int r,const vector<T> &a){
            if(l==r){
                tr[i].val = tr[i].maxh = a[l];
                return;
            }
            int mid = (l + r) >> 1;
            build(ls, l, mid, a);
            build(rs, mid+1, r, a);
            push_up(i);
        }

        void RESIZE(const int &N) { tr.resize(N<<2); }
        SegTree() = default;
        SegTree(const int &N): tr(N<<2) {}
        SegTree(const int &N, const vector<T> &a): tr(N<<2) { build(1, 1, N, a); }

    #endif

    // 单点修改
    void add_point(int i, int l, int r, int pos, T k) {
        if (l == r) {
            tr[i].maxh += k;
            tr[i].maxidx = l;
            return;
        }
        push_down(i, l, r);
        int mid = (l + r) >> 1;
        if (pos <= mid) add_point(ls, l, mid, pos, k);
        else add_point(rs, mid+1, r, pos, k);
        push_up(i);
    }

};
////////////////////////////////////////////////////////


void solve(){
    
    int n,m;
    cin >> n >> m;
    vector<vector<int>> e(n+1);
    for(int x,y,i=1;i<n;++i){
        cin >> x >> y;
        e[x].emplace_back(y);
        e[y].emplace_back(x);
    }

    /*
	    倍增LCA
    */
    vector<array<int,22>> bfa(n+1);
    vector<int> deep(n+1);
    auto init_beizeng = [&](int root){
        // init dfs
        auto dfs = [&](auto &&self, int u,int fa,int dep)->void{
            deep[u] = dep;
            bfa[u][0] = fa;
            for(auto &&v:e[u]){
                if(v == fa) continue;
                self(self, v, u, dep+1);
            }
        };
        dfs(dfs, root, 0, 0);

        // dp
        for(int i=1;(1<<i)<=n;++i){
            for(int j=1;j<=n;++j){
                bfa[j][i]=bfa[bfa[j][i-1]][i-1];
            }
        }
    };
    init_beizeng(1);
    // LCA
    auto LCA = [&](int x,int y){
        if(deep[x] < deep[y]) swap(x,y);
        while(deep[x] > deep[y]){
            x=bfa[x][int(log2(deep[x]-deep[y]))];
        }
        if(x==y) return x;
        for(int i=log2(deep[x]); i>=0; i--){
            if(bfa[x][i]!=bfa[y][i]){
                x=bfa[x][i],y=bfa[y][i];
            }
        }
        return bfa[x][0];
    };

    SegTree<int> seg(n); // n 个动态开点线段树
    const int N = 100000;
    for(int x,y,z,i=1;i<=m;++i){
        cin >> x >> y >> z;
        seg.add_point(x, 1, N, z, 1);
        seg.add_point(y, 1, N, z, 1);
        seg.add_point(LCA(x,y), 1, N, z, -1);
        seg.add_point(bfa[LCA(x,y)][0], 1, N, z, -1);
    }

    vector<int> ans(n+1);

    auto dfs = [&](auto &&self, int u, int fath) -> void{
        for(auto &&v: e[u]){
            if(v == fath) continue;
            self(self, v, u);
            seg.merge(u, v, 1, N);
        }
        if(seg.tr[u].maxh == 0) ans[u] = 0;
        else ans[u] = seg.tr[u].maxidx;
    };

    dfs(dfs, 1, 0);

    for(int i=1;i<=n;++i) cout << ans[i] << '\n';
    
}

int main(){
    
    cin.tie(nullptr)->sync_with_stdio(false);
    
    int _ = 1;
    // cin>>_;
    while(_--){
        
        solve();
        
    }
    
    return 0;
}
算法
数据结构 分块 线段树

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！