二分图最大匹配
参考blog:
PS:这里只放匈牙利找增广路径的算法,关于网络流请出门左拐网络流专题
一些定义
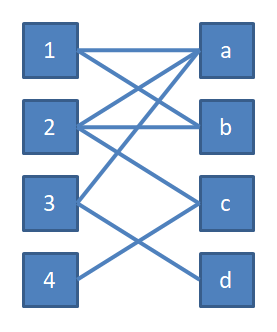
二分图:一个图的节点可以被分为两个互不相交的子集,且对于所有的边,其中一端的节点属于一个集合,另一端的节点属于另一个集合
匹配:图G的一个匹配是一组没有公共端点的不是圈的边构成的集合(重点:边的集合、任意两条边不能有公共顶点)
那么最大匹配就顾名思义了:匹配数最大的一个匹配(好像是废话)
完美匹配:若二分图X部的每一个顶点都与Y中的一个顶点匹配,并且Y部中的每一个顶点也与X部中的一个顶点匹配,则该匹配为完美匹配
因此,完美匹配一定是最大匹配,但最大匹配不一定是完美匹配(可以有点没有匹配)
完备匹配:一个二分图X部中的每一个顶点都与Y部中的一个顶点匹配,或者Y部中的每一个顶点也与X部中的一个顶点匹配,则该匹配为完备匹配
最佳匹配:带权二分图的权值最大的完备匹配称为最佳匹配(因此:最佳匹配不一定是最大匹配)
二分图判定
【模板题】二分图判定
染色法:从任意一个点开始DFS,将这个点标记为1,把连到的点标记为2(也可标记为别的),如果出现了当前点和相连点标记相同,则该图不是二分图
代码
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| int main(){
vector<int> colr(n+1);
function<bool(int,int)> isbg = [&](int u, int col) {
colr[u] = col;
for (auto &&v: e[u]) {
if (colr[u] == colr[v]) return false;
else if (!colr[v] && !isbg(v, 3 - col)) return false;
}
return true;
};
for(int i=1;i<=n;i++){
if(!col[i]){
if(!judge(i, 1)){
f = false;
break;
}
}
}
}
|
匈牙利算法
【模板题】二分图最大匹配
由于上面的blog已经讲得很详细了,我就不再赘述,这里总结一下核心步骤
核心步骤(找增广路径,找到则匹配数+1):
给一个点找匹配点,找到的另一个点有两种情况:
- 没有被匹配:那么就匹配上去
- 有其他点跟他匹配了:把那个其他点踹掉,递归地让他也执行这个点同样的操作,如果最后的点能回到情况1,就说明找到一条增广路径了(匹配数+1);否则当期点就无法匹配,跳过
时间复杂度:邻接表$O(n*m)$,邻接矩阵$O(n^3)$
注意事项:
- 记得要遍历二分图一侧的每一个点,每次都需要将
used数组重置为0
- 匹配找到之后,可根据题目要求选择是否要记录一下每个点匹配到的点的编号
- 如果给一般图做二分图最大匹配,由于双向边的存在,最终答案是
ans/2
代码
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| bool void Hungary(int x){
for(int i=1;i<=m;i++){
if(!used[i]&&gg[x][i]){
used[i]=1;
if(!have[i]||Hungary(have[i])){
have[i]=x;
have[x]=i;
return true;
}
}
}
return false;
}
bool Hungary(int u){
for(int i=head[u];~i;i=e[i].next){
int v=e[i].v;
if(!used[v]){
uesd[v]=1;
if(!have[v]||Hungary(have[v])){
have[v]=u;
return true;
}
}
}
return false;
}
int main(){
for(int i=1;i<=n;i++){
memset(used,0,sizeof(used));
if(Hungary(i)) ans++;
}
}
|
新姿势
如果你用上面的板子去搞这道题 洛谷 P1640 [SCOI2010]连续攻击游戏,你就会被无情地扣掉50分(TLE),原因:memset复杂度为O(n),太慢了!!!
因此,这里需要优化,我们考虑使用时间戳进行优化:
设置一个时间戳id,每次匹配时id++,在判断是否访问过时,改为used[v]!=id,下方也对应改为used[v]=id,然后就完工啦~
| ...
if(used[v]!=id){
used[v]=id;
...
}
...
for(int i=1;i<=n;i++){
id++;
if(Hungary(i)) ans++;
...
}
|
两个重要结论
【模板题】二分图最小点覆盖+最大独立集
- 二分图最小点覆盖

- 二分图最大独立集

- DAG图的最小路径覆盖数
DAG图的最小路径覆盖:用尽量少的不相交简单路径覆盖DAG的所有顶点
引理:DAG图的最小路径覆盖数=节点数(n)-最大匹配数(m)
二分图最大权匹配
参考bolg:
KM算法
KM算法的正确性基于以下定理:
若由二分图中所有满足A[i]+B[j]=w[i,j]的边(i,j)构成的子图(称做相等子图)有完备匹配,那么这个完备匹配就是二分图的最大权匹配
它是一个不断扩大相等子图的算法,只不过会将一侧点(通常为左侧)设立一个点标(权值为连出边的最大权值),在匹配的过程中如果无法增加匹配边了,就会尝试修改点标(左侧点减去,右侧点加上)来扩大相等子图,最后得到的一个完备匹配就是最佳匹配
时间复杂度:邻接矩阵$O(n^3)$
代码(板子)
【模板题】UOJ 二分图最大权匹配
上面是板子题,这里摘抄了一个UOJ里面的BFS板子(据说DFS会TLE)
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
| #include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<vector>
#define LL long long
using namespace std;
const int INF=0x3f3f3f3f;
const int mxn=411;
int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
void write(LL x){
if(x>9)write(x/10);
putchar(x%10+'0');
return;
}
inline int mini(int a,int b){return a<b?a:b;}
inline int maxi(int a,int b){return a>b?a:b;}
int nL,nR,bl,br,m;
int visL[mxn],visR[mxn];
int exL[mxn],exR[mxn];
int link[mxn],pre[mxn],lx[mxn];
int slack[mxn];
int mp[mxn][mxn];
LL ans=0;
int a[mxn];
int dtime=0;
int q[mxn<<1],hd,tl;
void Aug(int rt){
if(!rt)return;
link[rt]=pre[rt];
Aug(lx[pre[rt]]);
lx[pre[rt]]=rt;
return;
}
void BFS(int S){
int i,j,tmp;++dtime;
memset(slack,0x3f,sizeof slack);
hd=tl=1;q[tl]=S;
while(1){
while(hd<=tl){
int u=q[hd];++hd;
visL[u]=dtime;
for(int i=1;i<=nR;i++){
if(visR[i]^dtime){
tmp=exL[u]+exR[i]-mp[u][i];
if(!tmp){
visR[i]=dtime;pre[i]=u;
if(!link[i]){
Aug(i);
return;
}
q[++tl]=link[i];
}
else if(tmp<slack[i])slack[i]=tmp,pre[i]=u;
}
}
}
tmp=INF;
for(i=1;i<=nR;i++)if(visR[i]^dtime)tmp=mini(tmp,slack[i]);
for(i=1;i<=nL;i++){
if(visL[i]==dtime)exL[i]-=tmp;
if(visR[i]==dtime)exR[i]+=tmp;
else slack[i]-=tmp;
}
for(i=1;i<=nR;i++){
if(visR[i]^dtime && !slack[i]){
visR[i]=dtime;
if(!link[i]){
Aug(i);
return;
}
q[++tl]=link[i];
}
}
}
return;
}
void KM(){
for(int i=1;i<=nL;i++){
exL[i]=0;
for(int j=1;j<=nR;j++)
exL[i]=max(exL[i],mp[i][j]);
}
for(int i=1;i<=nL;i++) BFS(i);
ans=0;
nL=bl;nR=br;
for(int i=1;i<=nR;i++){
if(mp[link[i]][i]){
a[link[i]]=i;
ans+=mp[link[i]][i];
}
}
printf("%lld\n",ans);
for(int i=1;i<=nL;i++){
write(a[i]);
putchar(' ');
}
printf("\n");
return;
}
int main(){
int i,j;
nL=read();
nR=read();
bl=nL;br=nR;
nL=max(nL,nR);
nR=nL;
m=read();
int u,v,w;
for(i=1;i<=m;i++){
u=read();v=read();w=read();
mp[u][v]=w;
}
KM();
return 0;
}
|


