ST表浅析

---

ST表（稀疏表Sparse Table）

参考一位神犇的博客

功能

解决RMQ(Range Minimun/Maximun Query)问题的利器（当然也有别的更牛逼的方法，比如 树状数组or线段树）

复杂度：

• 预处理：$O(nlogn)$

• 查询：$O(1)$

算法

ST表利用的是倍增的思想（就是c++里面vector实现用的思想）

拿最大值来说，我们用$Max[i][j]$表示从$i$位置开始的$2^j$个数中的最大值，注意，这里的i代表区间左端点，而j代表2^j的区间长度，即$[i,i+2^j-1]$这个区间的最大值

ST表的构建类似一个区间dp的过程，首先枚举区间长度，再枚举区间左端点，最后进行状态转移，而转移过程如下：

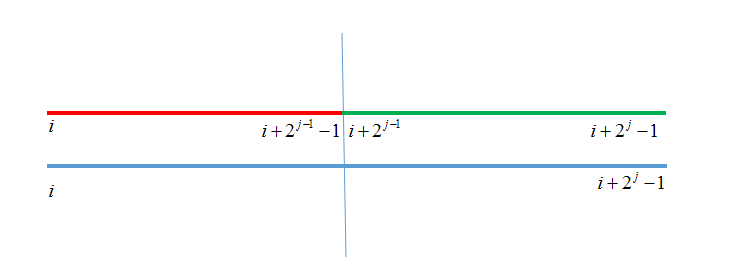
它将每个区间分为两段，分别比较两段的最大值更新到当前区间的最大值

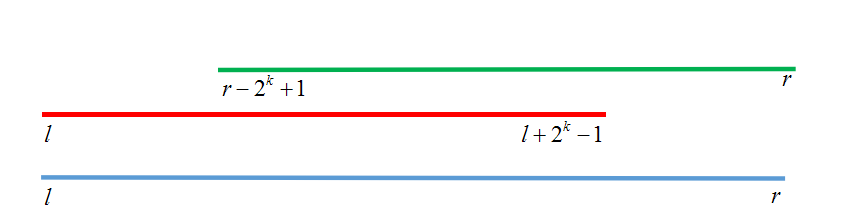
查询时，只需计算出$log_2(区间长度)$，然后根据左右端点分别查询一次取最大值即可，至于为什么要查询两次比较取最值，是因为$l+2^k-1$很有可能不是右端点（因为长度取对数取整了），同理$r-2^k+1$也可能不是左端点，但$[l,l+2^k-1]$he$[r-2^k+1,r]$这两个区间一定会有交集（如下图）

代码

注意事项：

• 预处理第一步切记要初始化：把$ST[i][0]$（从i位开始区间长为1，也就是序列本身）都设置为对应序列的原始值

• 区间长度的枚举范围（即ST表第二维的大小）取决于题目查询数据的范围，取$log2(查询范围)$就够用了

• 预处理时内层循环需要控制边界，右端点不能越界

预处理：

for(int i=1;i<=n;i++) ST[i][0]=a[i]; // 初始化
for(int j=1;(1<<j)<=n;j++){ //枚举区间长度
    for(int i=1;i+(1<<(j-1))-1<=n;j++){ //枚举左端点
        ST[i][j]=max/min(ST[i][j-1],ST[i+(1<<(j-1))][j-1]);
    }
}

查询：

inline int query(int l,int r){
    int len=log2(r-l+1);
    return max/min(ST[i][len],ST[r-(1<<len)+1][len]);
}

【模板】ST表代码：

#include<bits/stdc++.h>
using namespace std;
#define N 100005
int n,m,a[N],ST[N][23];

inline void init(){
	int len=log2(N);
	for(int j=1;j<=len;j++){
		for(int i=1;i+(1<<(j-1))-1<=n;i++){
			ST[i][j]=max(ST[i][j-1],ST[i+(1<<(j-1))][j-1]);
		}
	}
}
inline int query(int l,int r){
	int len=log2(r-l+1);
	return max(ST[l][len],ST[r-(1<<len)+1][len]);
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) 
		scanf("%d",&a[i]),ST[i][0]=a[i];
	init();
	int l,r;
	while(m--){
		scanf("%d%d",&l,&r);
		printf("%d\n",query(l,r));
	}
	return 0;
}