【补题系列】2020USST算法竞赛练习场9
题解
题意:
给出有n个节点和n-1条边的无向带权图(树),把边视为节点,节点视为边,构造一个新图,新图的边只存在于构成该边所连的两原图的边存在公共节点,边权为该边所连的原图的两边的边权之和,求这个新图的最小生成树(MST)
题解:
首先可以无脑想到,不就是求最小生成树嘛,建图然后prim或者kruskal走起呗
但问题是这个图怎么建?想破头皮没想出来于是逐渐开始放弃
因此我开始返璞归真,从最简单的情况看起,如下图(圆圈为原图)
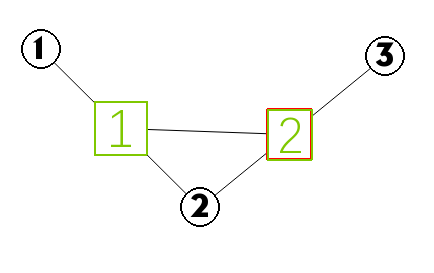
我们发现这时新图的MST就是一条单边,而且这两个节点是由原图的2节点的两条出边构成的,因此显然如果原图中一个节点只有一条出边,那么它肯定不能组成新图的一条边
再稍微复杂一点,看下图
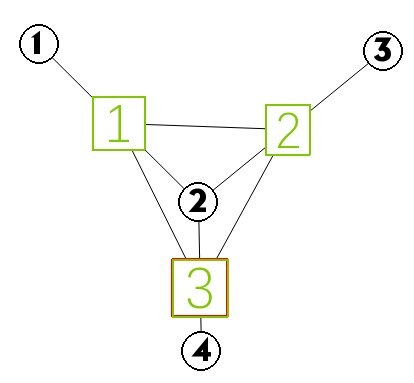
我们发现此时,2节点有三条出边,因此它代表了新图中的三条边,这个时候的MST就要取舍了,根据题意,新图的边权是原图对应两边权之和,那么显然我们只需要贪心地把原图该节点的最小出边设置为新图的“主节点”,然后把所有别的出边往主节点上连边就可以了,最后的边权和一定是最小的(因为我们反复往边权和里加的是原图最小的出边的边权)比如上图中如果dis[2][1]=1,dis[2][3]=2,dis[2][4]=3,那么21这条边就是对饮新图的主节点,对应的MST为dis[2][1]+dis[2][3]+dis[2][1]+dis[2][4],也就是所有出边求和 + (出边个数-2)*最小出边边权
因此,对于原图的每一个度不小于2的节点都重复上述操作就可以啦(不信可以自己建个图验证一下)
然而,此题还是有坑点(它似乎会卡常),以及请使用邻接表存图(用别的东西存可能会一直TLE)
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll inf=1ll<<60;
inline ll read() {
ll kk=0,f=1;
char cc=getchar();
while(cc<'0'||cc>'9'){
if(cc=='-')f=-1;
cc=getchar();
}
while(cc>='0'&&cc<='9'){
kk=(kk<<1)+(kk<<3)+cc-'0';
cc=getchar();
}
return kk*f;
}
ll n;
vector<ll> gg[200005];
int main(){
int t;t=read();
while(t--){
ll u,v,w;
n=read();
for(int i=1;i<=n;i++) gg[i].clear();
for(int i=1;i<n;i++){
u=read(),v=read(),w=read();
gg[u].push_back(w);gg[v].push_back(w);
}
ll ans=0;
for(int i=1;i<=n;i++){
ll temp=0,minh=inf,len=gg[i].size();
if(len<2) continue;
for(int j=0;j<len;j++){
temp+=gg[i][j];
minh=min(minh,gg[i][j]);
}
ans+=minh*(len-2)+temp;
}
printf("%lld\n",ans);
}
return 0;
}
|
题解
题意:
有若干正方形(以给出左下和右上的单位正方形的坐标形式给出),每次可以使任意一个正方形移动一步(上下左右),求满足使所有正方形都重合到一个单位正方形的最小步数
题解:
可以先考虑一维的情况,对于若干线段(左端点命名为l,右端点为r),现在需要找到一个点x,将所有线段平移到这个点上最小总步数就是下式
但这么写好像不太好找x,考虑换一种写法如下
去掉常数l-r和分母,在考虑简化一下,把l,r视为一个东西k,方程变为
也就是下面这个式子
这个x看起来像平均数or中位数,那么一个个试,ok确认过了是中位数
一个不严谨的证明:
我随便想了一个,先对k这个序列排序k1最小,kn最大,那么x理论上应该是处于k1~kn之间的一个数(这个太太太显然了,就不证了)那么
此时,直观上来看x为+1和为-1的次数应该相同(此时导数才得0),所以x取k[n/2]的时候是最好的,也就是中位数啦
因此这题只需要分别对横坐标和纵坐标排个序然后找到中位数所对应的坐标就是这题的x点了,剩下的就是模拟移过去的操作了
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll inf=1ll<<60;
struct node{
ll x1,y1,x2,y2;
}a[2000005];
ll x[500005],y[500005];
int main(){
int t;scanf("%d",&t);
while(t--){
int n;cin>>n;
int cnt1=0,cnt2=0;
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld%lld",&a[i].x1,&a[i].y1,&a[i].x2,&a[i].y2);
x[++cnt1]=a[i].x1;
x[++cnt1]=a[i].x2;
y[++cnt2]=a[i].y1;
y[++cnt2]=a[i].y2;
}
sort(x+1,x+1+cnt1);
sort(y+1,y+1+cnt2);
ll ans=0;
for(int i=1;i<=n;i++){
if(a[i].x1>x[n]||a[i].x2<x[n])
ans+=min(abs(x[n]-a[i].x1),abs(a[i].x2-x[n]));
if(a[i].y1>y[n]||a[i].y2<y[n])
ans+=min(abs(y[n]-a[i].y1),abs(a[i].y2-y[n]));
}
printf("%lld\n",ans);
}
return 0;
}
|
题解
题意:
给n个01的点,0之间连通,1之间连通,再给m条10之间连通的路,求从所有点到达每个点所走的最少步数和
题解:
分类讨论,总共有4种路线:
0到0或1到1,1步到位
0到1或1到0有公共路线,1步到位
0到1或1到0没有公共路线,但可以通过2步(先到有公共路线的地方,再走公共路线)到位;
0到1或1到0没有公共路线,只能通过3步(先到有公共路线的地方,再走公共路线,再走内部路线)
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read() {
ll kk=0,f=1;
char cc=getchar();
while(cc<'0'||cc>'9'){if(cc=='-')f=-1;cc=getchar();}
while(cc>='0'&&cc<='9'){kk=(kk<<1)+(kk<<3)+cc-'0';cc=getchar();}
return kk*f;
}
vector<ll> gg[10000005];
ll n,m,a[10000005];
ll zero,one,cnmd;
int main(){
n=read();
m=read();
for(ll i=1;i<=n;i++){
a[i]=read();
if(a[i]==0) zero++;
else one++;
}
for(ll i=1;i<=m;i++){
ll aa,bb;
aa=read();bb=read();
if(a[aa]!=a[bb]){
gg[aa].push_back(bb);
gg[bb].push_back(aa);
}
}
ll og=0,zg=0;
for(ll i=1;i<=n;i++){
if(gg[i].size()==0&&a[i]==0) zg++;
if(gg[i].size()==0&&a[i]==1) og++;
}
for(ll i=1;i<=n;i++){
ll ans=0;
if(a[i]==0){
ans+=zero-1+gg[i].size()+(n-zero-gg[i].size())*2;
}else if(a[i]==1){
ans+=one-1+gg[i].size()+(n-one-gg[i].size())*2;
}
if(gg[i].size()==0&&a[i]==0) ans+=og;
else if(gg[i].size()==0&&a[i]==1) ans+=zg;
if(i==1) printf("%lld",ans);
else printf(" %lld",ans);
}
return 0;
}
|
题解
题意:
求n条直线中有多少对直线至少有一个交点(重合也算有交点)
题解:
每条直线最多可以和前i-1条直线相交,然后减去斜率相同的直线个数,再加上斜率相同截距也相同的直线个数即可
Mark一下(第一道计算几何题)
- 此题为了避免精度问题,存的是斜率和截距的最简分数的形式
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll inf=0x3f3f3f3f;
typedef pair<ll,ll> pa;
inline ll read() {
ll kk=0,f=1;
char cc=getchar();
while(cc<'0'||cc>'9'){if(cc=='-')f=-1;cc=getchar();}
while(cc>='0'&&cc<='9'){kk=(kk<<1)+(kk<<3)+cc-'0';cc=getchar();}
return kk*f;
}
map<pair<pa,pa>,int> M;
map<pa,int> Mk;
ll n,t;
int main(){
ios::sync_with_stdio(false);
t=read();
while(t--){
M.clear();
Mk.clear();
n=read();
ll i;
ll ans=0;
for(i=1;i<=n;i++){
ll x1,y1,x2,y2;
x1=read(),y1=read(),x2=read(),y2=read();
ll ka=y1-y2,kb=x1-x2;
ll ba=x2*y1-x1*y2,bb=x2-x1;
ll gcdk=__gcd(abs(ka),abs(kb));
ll gcdb=__gcd(abs(ba),abs(bb));
pa k;
if(ka==0)
k=make_pair(0,0);
else if(kb==0)
k=make_pair(inf,inf);
else{
ka/=gcdk,kb/=gcdk;
if(ka*kb>0)
k=make_pair(abs(ka),abs(kb));
else
k=make_pair(-abs(ka),abs(kb));
}
pa b;
if(ba==0)
b=make_pair(0,0);
else if(bb==0)
b=make_pair(x1,x1);
else{
ba/=gcdb,bb/=gcdb;
if(ba*bb>0)
b=make_pair(abs(ba),abs(bb));
else
b=make_pair(-abs(ba),abs(bb));
}
ans+=(i-1-Mk[k]+M[make_pair(k,b)]);
Mk[k]++;
M[make_pair(k,b)]++;
}
cout<<ans<<endl;
}
return 0;
}
|
题解
题意:
有m个种类的糖果共n颗,每颗对应一个价值k,每种糖起购件数c(要么不买,要买就至少c个)求下式
题解:
本蒟蒻不太会,题解也看不太懂,先搁着
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read() {
ll kk=0,f=1;
char cc=getchar();
while(cc<'0'||cc>'9'){if(cc=='-')f=-1;cc=getchar();}
while(cc>='0'&&cc<='9'){kk=(kk<<1)+(kk<<3)+cc-'0';cc=getchar();}
return kk*f;
}
bool cmp(ll x,ll y){
return x>y;
}
vector<ll> cnmd[1000005],xbzz[1000005];
ll n,m,a[1000005];
int main(){
int t=read();
while(t--){
memset(a,0,sizeof(a));
n=read(),m=read();
for(ll i=1;i<=m;i++) a[i]=read();
for(ll i=0;i<n;i++){
ll x,y;
x=read(),y=read();
cnmd[y].push_back(x);
}
for(ll i=1;i<=m;i++){
sort(cnmd[i].begin(),cnmd[i].end(),cmp);
for(ll j=0;j<cnmd[i].size();j++){
xbzz[max(j+1,a[i])].push_back(cnmd[i][j]);
}
cnmd[i].clear();
}
ll giao=0,giaogiao=1,giaogiaogiao=0,giaogiaogiaogiao=0;
for(ll i=1;i<=n;i++){
giaogiaogiaogiao=i;
for(ll j=0;j<xbzz[i].size();j++){
giaogiaogiao+=xbzz[i][j];
}
if(giaogiao*giaogiaogiao>giao*giaogiaogiaogiao)
giaogiao=giaogiaogiaogiao,giao=giaogiaogiao;
xbzz[i].clear();
}
ll huohua=__gcd(giaogiao,giao);
printf("%lld/%lld\n",giao/huohua,giaogiao/huohua);
}
return 0;
}
|

