状压DP浅析

动态规划の状压dp

核心思想

  • 当我们有时无法用普通的dp以及一些算法表示一些状态、解决一些问题的时候，我们就可以想到状态压缩动态规划

  • 通常情况下，我们可以利用一个整数的二进制表示来表达一个状态

    如：101(5)，其中1表示该位处理过，0表示未处理（或一些别的物理意义）

    因此，我们便可以用一个整数来表示dp的状态，十分简便

  • 然而，由于该状态表示法十分吃空间（如一个状态有十个决策，那么就要用$2^{10}$这么大的数来表示所有可能的状态），因此使用状压的题一般数据范围都很小（十几的样子）

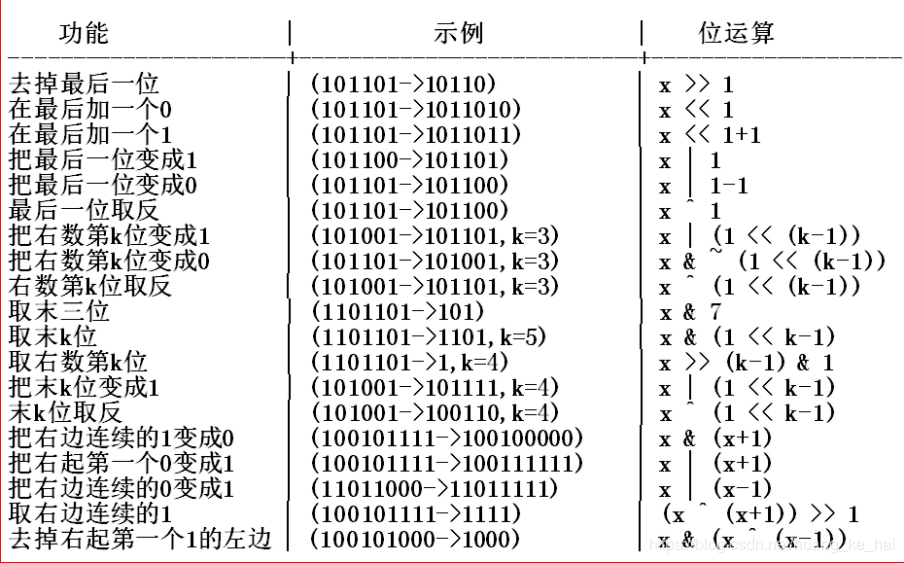
二进制状压操作

可以康康下图（网上复制来的，不太严谨，有的括号没加，要记住算术运算的优先级高于移位运算）

image.png

除此之外，一些最常用的操作如下：

  • 要求一行（or 一列）的状态不能有两个相邻

    1
    return !((x&(x<<1))||(x&(x>>1)));

  • 要求一行（or 一列）的状态不能间隔一个相邻

    1
    return !((x&(x<<2))||(x&(x>>2)));

  • 要求一行（or 一列）的状态不能连续三个相邻

    1
    return !(((x&(x<<1))&&(x&(x<<2)))||((x&(x>>1))&&(x&(x>>2))));

以此类推。。。总之就是本身和本身左移（或右移）若干位相与之后有没有重合的部分

  • 计算一个数的二进制位总共多少个1

__builtin_popcount()当然可以，但有时候会出玄学bug，慎用

下面的方法要牢记

1
2
3
4
5
6
7
8
inline int getnum(int x){
    int ans=0;
    while(x){
        ++ans;
        x-=(x&(-x)); //同lowbit操作
    }
    return ans;
}

一般的板子&优化操作

其实dp没有板子。。。

强行写一个最普通的吧

1
2
3
4
5
6
7
8
for(int i=1;i<n;i++){ //枚举每一行
    1.for(int j=1;j<=cnt) //如果预处理过状态总数，就用这个
    2.for(int j=0;j<1<<m;j++) //不担心时间复杂度的话，也可现在枚举所有状态
    {
        ...(各种嵌套循环和条件判断)
        dp[][]...=max/min(d[][]...,something) //转移
    }
}

优化的话，一般情况是爆空间（本蒟蒻只会这个），那么可以考虑预处理状态

1
2
3
4
5
int cnt,sta[];
for(int i=0;i<1<<m;i++){
    if(ok(i)) //ok函数用来判断该状态是否合理
        sta[++cnt]=i; 
}

以及滚动数组（对就是01背包里面那个滚动数组），即将一维开小，然后 根据当前状态需要前几个状态转移过来 来确定该维度大小，最后更新时只需取模即可

1
2
状态转移时：//需要前t个状态转移过来
    dp[i%t][]...=max/min(dp[i%t][]...,...)

习题

dp当然要多做题啦~

洛谷 P1879 玉米地

题意：给一个n*m的田地，有些地方可以种草地，要求种的草地不能相邻（没有公共边），求共有多少种种植方案？(答案模1e9)

题解：经典状压dp

定义dp[i][j]：处理到第i行状态为j时的方案总数，转移方程如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9;
int n,m,dp[15][1<<13],a[15][15];
int f[15];
inline bool ok(int x){
	return !(x&(x<<1)||x&(x>>1)); //判断状态是否满足不相邻
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			scanf("%d",&a[i][j]);
			if(a[i][j]==1) f[i]+=1<<(m-j);//把每行输入转为二进制状态
		}
//		printf("%d:%d\n",i,f[i]);
	}
	dp[0][0]=1;
	for(int i=1;i<=n;i++){
		for(int j=0;j<(1<<m);j++){ //枚举当前行状态
			if(ok(j)&&((j&f[i])==j)){ //右边这个是满足这块田可以种草地
				for(int k=0;k<(1<<m);k++){//枚举前一行状态
					if(ok(k)&&((k&j)==0)){//同上
						dp[i][j]=(dp[i][j]+dp[i-1][k])%mod;
					}
				}
			}
		}
	}
	int ans=0;
	for(int i=0;i<1<<m;i++) ans=(ans+dp[n][i])%mod; 
    //求所有可能方案数
	printf("%d\n",ans);
	
	return 0;
} //https://www.luogu.com.cn/problem/P1879

HDU 1565 方格取数

题意：给定一个n*n的非负数矩阵，你可以从中取出不相邻（没有公共边）的若干个数，求取出的数的最大的和

题解：经典状压dp

定义dp[i][j]：处理到第i行的状态为j时的取出的最大的和，转移方程如下，其中sum[j]为j状态取出数的和

这题数据范围有点大（<=20），因此需要预处理，否则T爆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll dp[21][1<<17];
ll a[21][21];
ll cnm[1<<17];
int n;
inline bool ok(int x){ //老骚操作了
	return (!(x&(x<<1))&&(!(x&(x>>1))));
}
inline int getsum(int row,int sta){ //获得当前行取数状态的和
	ll sum=0;
	for(int i=1;i<=n;i++){
		if(sta&(1<<i-1)) sum+=a[row][n-i+1];
	}
	return sum;
}
int main(){
	while(scanf("%d",&n)!=EOF){
		memset(dp,0,sizeof(dp));
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				scanf("%lld",&a[i][j]);
			}
		}
		int cnt=0;
		for(int i=0;i<1<<n;i++){ //预处理可行状态
			if(ok(i)) cnm[cnt++]=i;
		}
		
		for(int i=1;i<=n;i++){
			for(int j=0;j<cnt;j++){
				ll sum=getsum(i,cnm[j]); //获得和
				for(int k=0;k<cnt;k++){
					if((cnm[j]&cnm[k])==0){
						dp[i][j]=max(dp[i][j],dp[i-1][k]+sum);
					}
				}
			}
		}
		ll ans=0;
		for(int i=0;i<cnt;i++){ //千万别忘了这个
			ans=max(ans,dp[n][i]); //取最终状态中和最大的状态的答案
		}
		printf("%lld\n",ans);
	}
	return 0;
} //https://vjudge.net/problem/HDU-1565

洛谷 P1123 取数游戏

题意：跟上一题一样，只不过相邻的定义中改为 周围八个数

题解：同上，只不过枚举上一层时更新答案的条件需要改改了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll dp[7][1<<7];
ll a[7][7];
ll cnm[1<<7];
int n,m;
inline bool ok(int x){
	return (!(x&(x<<1))&&(!(x&(x>>1))));
}
inline int getsum(int row,int sta){
	ll sum=0;
	for(int i=1;i<=m;i++){
		if(sta&(1<<i-1)) sum+=a[row][m-i+1];
	}
	return sum;
}
int main(){
	int t;cin>>t;
	while(t--){
		cin>>n>>m;
		memset(dp,0,sizeof(dp));
		for(int i=1;i<=n;i++){
			for(int j=1;j<=m;j++){
				scanf("%lld",&a[i][j]);
			}
		}
		int cnt=0;
		for(int i=0;i<1<<m;i++){
			if(ok(i)) cnm[cnt++]=i;
		}
		
		for(int i=1;i<=n;i++){
			for(int j=0;j<cnt;j++){
				ll sum=getsum(i,cnm[j]);
				for(int k=0;k<cnt;k++){
// 如果当前行状态和上一行状态不移/左移/右移相与为0则合理
					if((cnm[k]&cnm[j])==0&&((cnm[k]<<1)&cnm[j])==0&&((cnm[k]>>1)&cnm[j])==0){
						dp[i][j]=max(dp[i][j],dp[i-1][k]+sum);
					}
				}
			}
		}
		ll ans=0;
		for(int i=0;i<cnt;i++){
			ans=max(ans,dp[n][i]);
		}
		printf("%lld\n",ans);
	}
	return 0;
} //https://www.luogu.com.cn/problem/P1123

洛谷 P1171 售货员的难题（旅行商问题）

题意：TSP问题，即求出从起点出发访问图中所有点再回到起点的最短路

题解：超级经典的NP完全问题，数据量大的话只能用一些选学算法来搞，不过如果数据量小的话，就可以用强大的状压dp啦

定义状态dp[i][j]：访问情况为i状态时当前在j这个节点的最短路，其中状态用二进制整数表示，1表示该节点走过，0表示未走过，那么显然有状态转移方程（其中dis为图的邻接矩阵，值为两点间距离）

那么最终答案就是

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9;
const int inf=1<<30;
int n,dp[1<<20][25];
int a[25][25];
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			scanf("%d",&a[i][j]);
		}
	}
	memset(dp,67,sizeof(dp));//求最小值，dp初始化为最大
	dp[1][1]=0;//初始状态
	for(int i=0;i<1<<n;i++){//枚举当前状态
		for(int j=1;j<=n;j++){//枚举每个节点
			if(!((1<<(j-1))&i)){//如果这个节点没走过
				for(int k=1;k<=n;k++){//枚举每个节点
					if((1<<(k-1))&i)//如果走过，则个可用它更新j
						dp[i|(1<<(j-1))][j]=min(dp[i|(1<<(j-1))][j],dp[i][k]+a[k][j]); //愉快地更新j
				}
			}
		}
	}
	int ans=inf;
    //取所有合法状态的最短路
	for(int i=2;i<=n;i++) ans=min(ans,dp[(1<<n)-1][i]+a[i][1]);
	printf("%d\n",ans);
	return 0;
}  //https://www.luogu.com.cn/problem/P1171

洛谷 P2622 关灯问题Ⅱ

题意：见链接（已经够简洁了）

题解：状压dp，按照 灯的状态 、按下每个按钮、按下按钮后每个灯的变化情况枚举，就一定能枚举到所有情况，用按下按钮后的状态来更新按下之前的状态即可

定义dp[i]：灯在i状态下最少需要按下的按钮次数，则转移方程为

最后处理一下不存在的情况即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<bits/stdc++.h>
using namespace std;
int dp[1<<15];
int a[105][15];
int n,m;
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
		for(int j=1;j<=n;j++)
			scanf("%d",&a[i][j]);
	memset(dp,0x3f,sizeof(dp));//初始化
	dp[(1<<n)-1]=0;//一开始全开着灯，不需要按
	for(int i=(1<<n)-1;i>=0;i--){//注意枚举顺序
		for(int j=1;j<=m;j++){//枚举按钮
			int now=i; //这个now稍后会变成按之后的状态，便于转移
			for(int k=1;k<=n;k++){//枚举处理每个灯的变化
				if(a[j][k]==0) continue;//不变
				else if(a[j][k]==1){//如果开着，把它关了
					if(i&(1<<n-k)) now=now^(1<<n-k);//该位取反操作
				}else if(a[j][k]==-1){//如果关着，把它开开
					if(!(i&(1<<n-k))) now=now^(1<<n-k);//同上
				}
			}
			dp[now]=min(dp[now],dp[i]+1);//转移
		}
	//如果不存在（这个奇怪的数就是memset 0x3f之后的数），输出-1
	printf("%d\n",dp[0]==1061109567?-1:dp[0]);
	return 0;
}

洛谷 P2704 炮兵阵地

题意：给一个n*m的矩阵，有些地方可以建炮塔，炮塔可以打上下左右两个格子的地方，求不误伤友军的前提下最多可以建多少炮塔

题解：稍微有点恶心的状压dp，恶心就恶心在每一行的状态是由前两行决定的，因此我们的dp方程需要多开一维

定义dp[i][j][k]：处理到第i行时第i行为j状态且第i-1行为k状态的最多炮塔总数，那么显然状态转移方程如下

注意初始化时需要初始化第一行和第二行的所有状态，然后从第三行开始递推，虽然维数较多，预处理肯定是需要的，但亲测不用滚动数组也可AC

下面上代码（这个for循环给爷写吐了）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#include<bits/stdc++.h>
using namespace std;
int n,m,a[105];
char mm[105][35];
int dp[105][70][70];
int sta[70],cnt;
int num[300];
inline bool ok(int x){//常规操作
	if(!((x&x<<1)||(x&x>>1)||(x&x<<2)||(x&x>>2))) return true;
	return false;
}

inline int getnum(int x){ //常规操作
	int ans=0;
	while(x){
		ans++;
		x-=(x&(-x));
	}
	return ans;
}

int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>mm[i][j];
			if(mm[i][j]=='H') a[i]|=1<<m-j; //输入转状态
		}
//		cout<<a[i]<<endl;
	}
	
	for(int i=0;i<1<<m;i++){//预处理状态
		if(ok(i)){
//			cout<<i<<endl;
			sta[++cnt]=i;
			num[cnt]=getnum(i);//预处理该状态的和
		}
	}
//	cout<<cnt<<endl;
	
	for(int i=1;i<=cnt;i++){//初始化第一行
		if((sta[i]&a[1])==0){ //不与地图冲突就可
			dp[1][i][0]=num[i];
//			cout<<dp[1][i][0]<<endl;
		}
	}
//	exit(0);
	for(int i=1;i<=cnt;i++){//初始化第二行
		if((sta[i]&a[2])==0){
			for(int j=1;j<=cnt;j++){
				if((sta[j]&a[1])==0&&(sta[j]&sta[i])==0){
					dp[2][i][j]=num[i]+num[j];
				}
			}
		}
	}
//	exit(0);
    //这个for循环惊了
	for(int i=3;i<=n;i++){//从第三行开始
		for(int j=1;j<=cnt;j++){
			if((sta[j]&a[i])==0){
				for(int k=1;k<=cnt;k++){
					if((sta[j]&sta[k])==0&&(sta[k]&a[i-1])==0){
						for(int l=1;l<=cnt;l++){
                            //这个条件判断真长
							if((sta[l]&sta[j])==0&&(sta[l]&sta[k])==0&&(sta[l]&a[i-2])==0){
								dp[i][j][k]=max(dp[i][j][k],dp[i-1][k][l]+num[j]);
							}
						}
					} 
				}
			}
		}
	}
//	exit(0);
	int ans=0;
	for(int i=1;i<=cnt;i++){//获取最大数目
		for(int j=1;j<=cnt;j++){
			ans=max(ans,dp[n][i][j]);
		}
	}
	printf("%d\n",ans);
	return 0;
} //https://www.luogu.com.cn/problem/P2704

感想：感觉没区间dp那么玄学（前提是二进制操作非常熟练），但是题目感觉可以难上天

算法
动态规划

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！