图论算法の拓扑排序
拓扑序定义
对于一个$DAG$(有向无环图)$G$,它的拓扑序是该图所有节点的一个线性序列,该序列必须满足使得图中的任意一对顶点$u$和$v$,若边$ (u,v) \in E(G) $,则$u$在线性序列中出现在$v$之前
算法流程
对于一个$DAG$:
- 将所有入度为0的节点加入队列中
- 每次将队首元素(节点)出队并将其所有的出边砍掉(即 把该出边所连节点的入度减一),这样以后如果出现了新的入度为0的节点,那么把他们加入队列,重复该步骤,直到队列为空
- 每次出队的队首元素的顺序就是该图的一种拓扑序(答案不唯一,因为可能会同时存在好几个入度为0的节点,他们互不影响)
举个例子,如下一张图
我们首先将入度为0的点入队(1、4),此时拓扑序还未构建
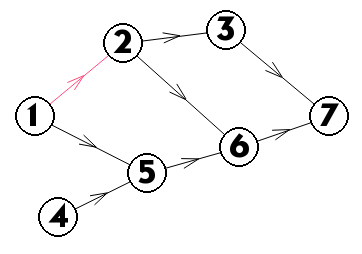
然后删去他们的出边,并判断出边所连节点是否入度为0
此时拓扑序为:1 4
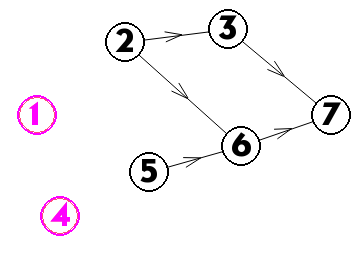
发现2、5节点的入度变为0了,于是入队,重复上一步操作
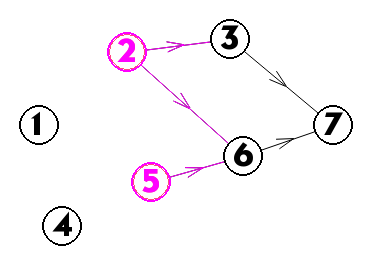
此时拓扑序为:1 4 2 5
删去2 5节点的出边后,发现3 6节点入度变为0,于是入队
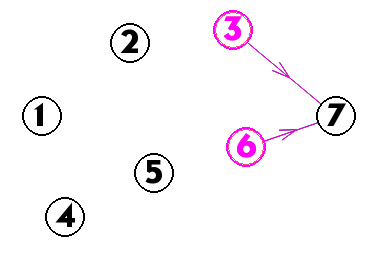
取出3 6之后,拓扑序为:1 4 2 5 3 6
这时发现7入度为0,于是入队
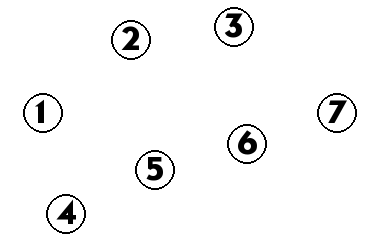
最后结束,拓扑排序最终结果为:1 4 2 5 3 6 7(答案不止这一种,可以很容易算出此题答案有8种)
实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| #include<bits/stdc++.h>
using namespace std;
struct Edge{
int u,v,next;
}e[100005];
int n,m,cnt,head[100005],indeg[100005];
inline void addedge(int u,int v){
e[++cnt].u=u;
e[cnt].v=v;
e[cnt].next=head[u];
head[u]=cnt;
}
int ans[100005],ccnt;
inline void topo_sort(){
queue<int> q;
for(int i=1;i<=n;i++){
if(indeg[i]==0){
q.push(i);
}
}
while(!q.empty()){
int u=q.front();
q.pop();
ans[++ccnt]=u;
for(int i=head[u];i;i=e[i].next){
int v=e[i].v;
if(indeg[v]){
indeg[v]--;
if(indeg[v]==0){
q.push(v);
}
}
}
}
}
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++){
int u,v;
scanf("%d %d",&u,&v);
addedge(u,v);
indeg[v]++;
}
topo_sort();
for(int i=1;i<=ccnt;i++){
cout<<ans[i]<<" ";
}
return 0;
}
|
题意
- 给一个DAG图重新编号并排序,使得对于该序列中任意的两点$i$$j$且$i<j$,满足新编号$a[i]<a[j]$
题解
- 考虑反向建图做一个逆拓扑排序,并且使用优先队列维护每次出队的都是最大的编号的节点,同时逆向编号即可得出答案
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #include<bits/stdc++.h>
using namespace std;
struct Edge{
int u,v,next;
}e[1000005];
int n,m,cnt,head[1000005],indeg[1000005];
inline void addedge(int u,int v){
e[++cnt].u=u;
e[cnt].v=v;
e[cnt].next=head[u];
head[u]=cnt;
}
int ans[1000005];
inline void tpsort(){
priority_queue<int> q;
for(int i=1;i<=n;i++){
if(indeg[i]==0){
q.push(i);
}
}
int num=n;
while(!q.empty()){
int u=q.top();
q.pop();
ans[u]=num--;
for(int i=head[u];i;i=e[i].next){
int v=e[i].v;
if(indeg[v]){
indeg[v]--;
if(indeg[v]==0){
q.push(v);
}
}
}
}
}
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++){
int u,v;
scanf("%d %d",&u,&v);
addedge(v,u);
indeg[u]++;
}
tpsort();
for(int i=1;i<=n;i++){
printf("%d ",ans[i]);
}
return 0;
}
|




