并査集板子&习题
[toc]
并査集
概念
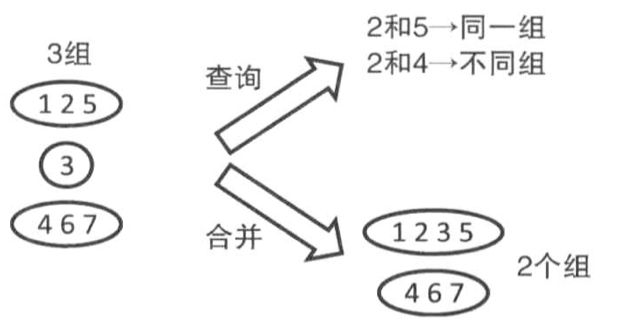
- 并査集是一种用来管理元素分组的数据结构,可以高效地进行如下操作:
- 查询元素$a$和元素$b$是否属于同一组
- 合并元素$a$和元素$b$所在的组
实现
步骤:
初始化:准备$n$个节点来表示$n$个元素(没有边,每个元素都是独立的)
| inline void init(){
for(int i=1;i<=n;i++){
fa[i]=i;
ran[i]=1;
}
}
|
查询元素所在的组:从元素开始沿着树向上走到根部,判断两个根是否相同即可
优化:采用路径压缩,即把每个元素都连向根节点
| inline int find(int x){
return f[x]==x?x:fa[x]=find(fa[x]);
}
|
查询两元素是否在同一组:
| inline bool same(int x,int y){
return find(x)==find(y);
}
|
合并两元素所在组:从一个组的根向另一个组的根连边
| inline void unite(int x,int y){
fa[find(x)]=find(y);
}
|
优化:按秩合并,用一个数组$ran$记录每组的深度(秩),每次连边让深度小的向深度大的连边
| inline void unite(int x,inty){
x=find(x);
y=find(y);
if(x==y) return;
if(ran[x]<ran[y]){
fa[x]=y;
}else{
fa[y]=x;
if(ran[x]==ran[y]) ran[x]++;
}
}
|
或者:一般情况下,直接不考虑深度的按秩合并就够用了
| inline void unite(int x,int y){
x=find(x);
y=find(y);
if(x!=y){
fa[x]=y;
ran[y]+=x;
}
}
|
并査集扩展应用
二维并査集
其实就是在普通的一维并査集基础上加了一个维度罢了,没什么稀奇的,有的题目可能会有好几种不同的集合需要维护,这个时候开一个二维的并査集来维护就可以啦
例题:CF 505B
带权并査集
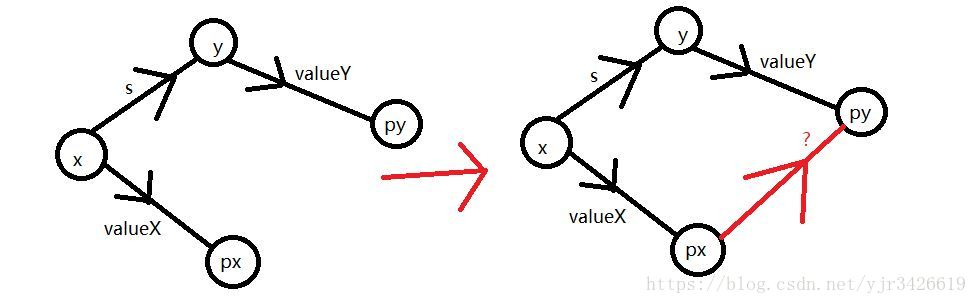
顾名思义,带权并査集就是并査集中点的“连线”(或者节点)具有权值和方向,此时并査集更像是一颗树,通常用来维护元素之间的相对关系(如:相对大小、类别 等)下面是一些模板操作
- 查询(路径压缩),可以发现代码中先存了当前父节点的编号,递归完成后,所有父节点都连到了根节点,那么当前节点的权值就应该是自己和父节点权值的和,而对于父节点也是一样,递归操作就能达到这样的效果
| inline int find(int x){
if(x!=fa[x]){
int t=fa[x];
fa[x]=find(fa[x]);
val[x]=(val[x]+val[t])%k;
}
return fa[x];
}
|
通常情况下是按照同一点通过不同路线连到根节点的权值相同的原理来合并权值
但具体情况视题目而定
| inline void unite(int x,int y,int value){
int px=find(x);
int py=find(y);
if(px!=py){
fa[px]=py;
val[px]=(value+val[y]-val[x])%k;
}
}
|
习题
题意
说实话前面两题应该放到最后的(因为最难。。)
见题目链接
思路&题解
- 普通并査集解法(三倍空间并査集)
- 使用并査集,维护$ABC$三组数据(用同一个数组实现,只需要下标表示为$i,i+N,i+2N$即可),$X-A/B/C$代表$X$属于$A/B/C$类
- 若有:$1 X Y$,则先检查有没有($X-A$且$Y-B$)或($X-A$且$Y-C$),若无误则同时令$X-A\ Y-A$, $X-B\ Y-B$,$X-C\ Y-C$,这样就可以确保所有情况都考虑到
- 若有:$2 X Y$,则先检查有没有($X-A$且$Y-A$)或($X-A$且$Y-C$),若无误则同时令$X-A\ Y-B$,$X-B\ Y-C$,$X-C\ Y-A$
- 带权并査集解法(维护三个种类,并査权值时取模)
AC代码(三倍空间并査集)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| #include<iostream>
#include<cstdio>
using namespace std;
int par[500005];
int rank[500005];
void init(int n){
for(int i=0;i<n;i++){
par[i]=i;
rank[i]=0;
}
}
int find(int x){
if(par[x]==x) return x;
else return par[x]=find(par[x]);
}
void unite(int x,int y){
x=find(x);
y=find(y);
if(x==y) return;
if(rank[x]<rank[y]) par[x]=y;
else{
par[y]=x;
if(rank[x]==rank[y]) rank[x]++;
}
}
bool same(int x, int y){
return find(x)==find(y);
}
int main(){
int n,k;
scanf("%d %d",&n,&k);
init(3*n);
int ans=0;
for(int i=1;i<=k;i++){
int x,a,b;
scanf("%d %d %d",&x,&a,&b);
a=a-1,b=b-1;
if(a>=n||b>=n){
ans++;
continue;
}
if(x==1){
if(same(a,b+n)||same(a,b+2*n)){
ans++;
continue;
}else{
unite(a,b);
unite(a+n,b+n);
unite(a+2*n,b+2*n);
}
}
if(x==2){
if(same(a,b)||same(a,b+2*n)){
ans++;
continue;
}else{
unite(a,b+n);
unite(a+n,b+2*n);
unite(a+2*n,b);
}
}
}
printf("%d\n",ans);
return 0;
}
|
题意
见题目链接
思路&题解
- 一开始看是个并査集裸题,对$e$排序把合并操作($e==1$的情况)放在前面先做好,然后开始遍历$e==0$的情况判断是否矛盾即可,然后做的时候发现数组范围是$1e9$
(可以骗70分左右),开不了这么大的数组怎么办?
考虑离散化,三部曲:
- 对原数组排序
- $unique$函数去重
- lower_bound更新原数组位置
这样数组规模就可以压缩到$2n$大小,足够了
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include<bits/stdc++.h>
using namespace std;
struct node{
int x,y,e;
}a[1000005];
bool cmp(node x1,node x2){
return x1.e>x2.e;
}
int fa[1000005],b[5000005];
set<int> se;
inline int find(int x){
return x==fa[x]?x:fa[x]=find(fa[x]);
}
inline void unite(int x,int y){
fa[find(x)]=find(y);
}
inline void init(int n){
for(int i=1;i<=n;i++){
fa[i]=i;
}
}
int main(){
int n;
cin>>n;
while(n--){
bool f=true;
int m;
cin>>m;
int tot=0;
for(int i=1;i<=m;i++){
cin>>a[i].x>>a[i].y>>a[i].e;
b[++tot]=a[i].x;
b[++tot]=a[i].y;
}
sort(b+1,b+tot+1);
int unq = unique(b+1,b+tot+1)-b-1;
for(int i=1;i<=m;i++){
a[i].x = lower_bound(b+1,b+1+unq,a[i].x)-b;
a[i].y = lower_bound(b+1,b+1+unq,a[i].y)-b;
}
init(unq);
sort(a+1,a+1+m,cmp);
for(int i=1;i<=m;i++){
if(a[i].e==1) unite(a[i].x,a[i].y);
else{
if(find(a[i].x)==find(a[i].y)){
f=false;
break;
}
}
}
if(f) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}
|
题意
给个无向图,每条边用一个整数表示一种颜色,有若干次询问,每次询问一对节点之间能通过一种颜色连通的种类数
题解
开一个二维并査集,第一维维护每种颜色,第二维维护每种颜色对应的集合,询问时只需遍历第一维找对应两节点的根是不是同一个即可
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| #include<bits/stdc++.h>
using namespace std;
int n,m,q,fa[125][125];
inline void init(){
for(int i=1;i<=105;i++){
for(int j=1;j<=105;j++){
fa[i][j]=j;
}
}
}
inline int find(int c,int y){
return fa[c][y]==y?y:fa[c][y]=find(c,fa[c][y]);
}
inline void unite(int x,int y,int c){
x=find(c,x);
y=find(c,y);
if(x!=y) fa[c][y]=x;
}
int main(){
cin>>n>>m;
init();
int u,v,w;
for(int i=1;i<=m;i++){
cin>>u>>v>>w;
unite(u,v,w);
}
cin>>q;
for(int i=1;i<=q;i++){
cin>>u>>v;
int ans=0;
for(int j=1;j<=m;j++){
if(find(j,u)==find(j,v)){
ans++;
}
}
cout<<ans<<endl;
}
return 0;
}
|
题意
一个矩形地图上有若干炸弹,如果引爆一颗,则其横着竖着的所有炸弹都会被引爆,产生连锁反应,问最少需要引爆几次才能炸完所有炸弹?
题解
建立一个并査集维护行和列的关系,可以另外开辟一个空间维护列,这样只要在输入的时候把对应点的行列合并,最后处理的时候横纵坐标单独处理(如果该点对应的行、列没被标记,则标记这一行、列)
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| #include<bits/stdc++.h>
using namespace std;
const int inf=2147483647;
int n,m,shen[5005],vis[5005],fa[5005];
char a[5005][5005];
inline void init(){
for(int i=1;i<=n+m+2;i++){
fa[i]=i;
}
}
inline int find(int x){
return x==fa[x]?x:fa[x]=find(fa[x]);
}
inline void unite(int x,int y){
x=find(x);
y=find(y);
fa[x]=y;
}
int main(){
scanf("%d%d",&n,&m);
init();
for(int i=0;i<n;i++){
scanf("%s",a[i]);
}
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(a[i][j]=='1'){
unite(i,j+n);
}
}
}
int ans=0;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(a[i][j]=='1'){
if(!vis[find(i)]){
vis[find(i)]=1;
ans++;
}
if(!vis[find(j+n)]){
vis[find(j+n)]=1;
ans++;
}
}
}
}
printf("%d\n",ans);
return 0;
}
|
题意
给出若干个“区间左端点 区间右端点 区间和”的申明,问有几个申明与之前的声明冲突(错误)
题解
带权并査集的经典问题,此题有两个注意事项
- 维护开区间,因为闭区间无法维护,比如给出
[1,5],[3,5]的区间和,问[1,2]的区间和,并査集中根本就没有2这个点,所以需要考虑把区间的一端设置为开区间,上例可以改为给出(0,5],(2,5],问(0,2]的区间和
- 带权并査集的处理,连线的方向由左端点连向右端点,这样就可以用
val[左端点]-val[右端点]的方式求出区间和
PS:这东西很像前缀和
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,m,fa[200005],val[200005];
inline void init(){
for(int i=0;i<=n;i++){
fa[i]=i;
}
}
inline int find(int x){
if(x!=fa[x]){
int t=fa[x];
fa[x]=find(fa[x]);
val[x]+=val[t];
}
return fa[x];
}
inline void unite(int x,int y,int value){
int fx=find(x);
int fy=find(y);
if(fx!=fy){
fa[fx]=fy;
val[fx]=value+val[y]-val[x];
}
}
int main(){
while(~scanf("%d%d",&n,&m)){
memset(val,0,sizeof(val));
int ans=0;
init();
for(int i=1;i<=m;i++){
int x,y,z;
cin>>x>>y>>z;
--x;
int fx=find(x);
int fy=find(y);
if(fx==fy){
if(val[x]-val[y]!=z){
ans++;
}
}else{
unite(x,y,z);
}
}
cout<<ans<<endl;
}
return 0;
}
|
题意
给出若干对同学的相对得分差(A比B高xx分),然后有若干次询问,每次询问给出两个同学,问能否知道他们的相对得分差?
题解
带权并査集维护相对关系(和上一题是重题?)
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int val[100005],fa[100005],n,m,q;
inline void init(){
for(int i=1;i<=n;i++) fa[i]=i;
}
inline int find(int x){
if(x!=fa[x]){
int t=fa[x];
fa[x]=find(fa[x]);
val[x]+=val[t];
}
return fa[x];
}
inline void unite(int x,int y,int value){
int fx=find(x);
int fy=find(y);
if(fx!=fy){
fa[fx]=fy;
val[fx]=val[y]+value-val[x];
}
}
int main(){
scanf("%d%d%d",&n,&m,&q);
init();
int x,y,z;
for(int i=1;i<=m;++i){
scanf("%d%d%d",&x,&y,&z);
unite(x,y,z);
}
for(int i=1;i<=q;++i){
scanf("%d%d",&x,&y);
if(find(x)!=find(y)){
printf("-1\n");
}else{
printf("%d\n",val[x]-val[y]);
}
}
return 0;
}
|
题意
给出若干对昆虫的性别关系(两个两个给出,每一对都互为异性),求给出的这些数据中有没有冲突
题解
带权并査集维护种类关系,权值为1代表异性,0代表同性,找规律易得合并和查询时权值更新只需求和再对2取模即可
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int val[2005],fa[2005],n,m,t;
inline void init(){
memset(val,0,sizeof(val));
for(int i=1;i<=n;i++) fa[i]=i;
}
inline int find(int x){
if(x!=fa[x]){
int t=fa[x];
fa[x]=find(fa[x]);
val[x]=(val[x]+val[t])%2;
}
return fa[x];
}
int main(){
scanf("%d",&t);
for(int o=1;o<=t;++o){
bool f=true;
scanf("%d%d",&n,&m);
init();
int x,y;
for(int i=1;i<=m;++i){
scanf("%d%d",&x,&y);
int fx=find(x),fy=find(y);
if(fx!=fy){
fa[fx]=fy;
val[fx]=(val[y]+1-val[x]+2)%2;
}else{
if((val[x]-val[y]+2)%2==0){
f=false;
}
}
}
printf("Scenario #%d:\n",o);
if(f) printf("No suspicious bugs found!\n");
else printf("Suspicious bugs found!\n");
}
return 0;
}
|

