链式前向星解释

存图方式：链式前向星 浅析

• 我们目前所知的存图方式有三种：
  1. 邻接矩阵
  2. 邻接表
  3. 链式前向星

然而邻接矩阵空间复杂度太大，除了一些特定场合（$floyd$算法等）需要使用之外并不推荐；邻接表不太好建出来，因此大多是情况下我们使用链式前向星的方式来存储图结构，下面做一点解释。

---

链式前向星

• 与邻接矩阵 存储一对节点和这对节点的权值 的方式不同，链式前向星采用的方式是存储每一条边。

• 这一条边包含了以下信息：

  • 从哪来（起点）
  • 到哪去（终点）
  • 权值
  • $next$值：与本条边相同起点的前一条边

• 个人理解：仿佛把每一个节点出发的所有边存储在了以该节点命名的链表内。

实现过程

• 首先是一条边（$Edge$）的结构定义如下：

  struct edge{
  	int from,to,next,dis;
  };

• 开辟一些变量（用来计数和用于遍历，很重要）

  int head[1000005]; //用来存从每个节点出发的最后一条边的序号
  int cnt; //用来记录边的序号

• $addedge$函数:

  void addedge(int u,int v,int w){
  	cnt++;
      edge[cnt].from = u;
      edge[cnt].to = v;
      edge[cnt].dis = w;
      edge[cnt].next = head[u]; //把这条边和同一起点的上一条边接上
      head[u] = cnt; //更新当前起点所对应的最后一条边的序号
      return;
  }

• 示例：

  Sample Input

  1 2 3
  1 3 2
  2 3 1
  2 4 5
  3 4 4

  构建了如下的一个图：

  

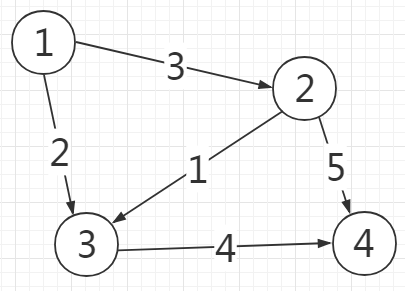
  每次$addedge$操作中，最后两行（带有注释的）代码所进行的过程如下：

  举个例子，现在第1条边（1，2）已经连上，需要$addedge(1,3,2)$：

  

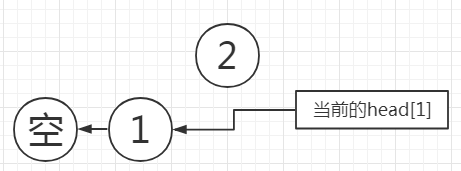
  1. 将当前$edge$与同起点的上一条$edge$连上：

     

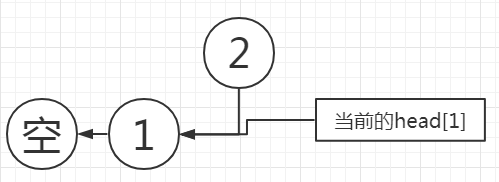
  2. 将$head$更新为指向当前同起点的最后一条$edge$，也就是现在这一条$edge$：

     

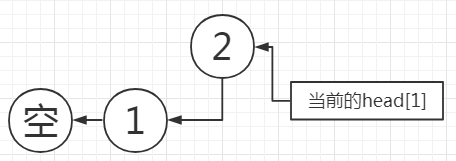
  大功告成，接下来按照同样步骤把图存完即可，最终结果如下图所示：

  

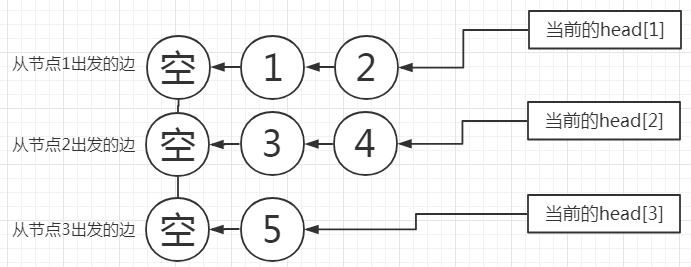
  PS：如果是无向图的话，那么就$addedge(u,v,w)$再$addedge(v,u,w)$即可。

图的遍历

• 链式前向星能够优化图的遍历过程，如$Dijkstra$、$DFS$、$BFS$等，其最简单的遍历方式如下：（枚举每一个点的所有的边（倒序））

  for(int p=head[i];p;p=edge[p].next){ //i号节点
  	...
  }

---