单调栈&单调队列
[刷题记录]单调栈&单调队列练习
- 最近学到单调栈&单调队列,题目也开始有点考验思维了,下面做简单介绍。
单调栈
概念
- 顾名思义,就是满足单调性的栈结构,可以是单调递增or递减or自己定义。
实现(核心代码)
| while(!stack.empty() && x > stack.top()){
stack.pop();
}
stack.push(x);
|
练习题
题意
- 有$N$头牛从左到右排成一排,每头牛有一个高度为$hi$,设左数第$i$头牛与「它右边第一头高度$\geq h_i$」的牛之间有$c_i$头牛,试求$\sum ^{N}{i=1}c_{i}$。
题解
- 应用单调栈的思想,由于牛头都是朝着右边看,所以把输入的每头牛倒序压入一个单调不增的单调栈中,每次需要弹出元素时需要处理一下答案。
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #include<cstdio>
#include<iostream>
#include<stack>
using namespace std;
typedef long long ll;
ll a[100005];
stack<ll> s;
ll ans[100005];
int main(){
ll n;
cin>>n;
for(ll i=1;i<=n;i++){
cin>>a[i];
ans[i]=1;
}
for(ll i=n;i>=1;i--){
while(!s.empty()&&a[i]>a[s.top()]){
ans[i]+=ans[s.top()];
s.pop();
}
s.push(i);
}
ll anss=0;
for(ll i=1;i<=n;i++) anss+=ans[i];
cout<<anss-n<<endl;
return 0;
}
|
题意
题解
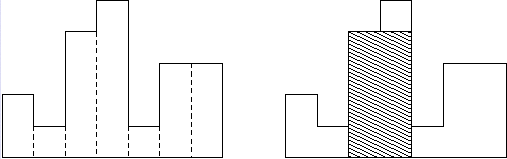
- 我们发现,直方图的每一小段都对应着一个最大矩形,那么我们可以通过求这些矩形的最大值来求出答案;
- 具体的每一段最大矩形的求法:应用严格单调递增的单调栈按照上一题的方式,先从左往右撸一遍直方图,再从右往左撸一遍,把两次单调栈的答案记录下来并求和再减1,就得到了每一段对应的最大宽度,最后再乘以长度并求$max$即可。
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| #include<iostream>
#include<stack>
#include<cstdio>
using namespace std;
typedef long long ll;
ll a[100005];
ll ans1[100005],ans2[100005];
ll ans;
stack<ll> s;
int main(){
ll n;
while(cin>>n&&n){
ans=0;
while(!s.empty()) s.pop();
for(ll i=1;i<=n;i++){
scanf("%lld",&a[i]);
ans1[i]=ans2[i]=1;
}
for(ll i=1;i<=n;i++){
while(!s.empty()&&a[i]<=a[s.top()]){
ans1[i]+=ans1[s.top()];
s.pop();
}
s.push(i);
}
while(!s.empty()) s.pop();
for(ll i=n;i>=1;i--){
while(!s.empty()&&a[i]<=a[s.top()]){
ans2[i]+=ans2[s.top()];
s.pop();
}
s.push(i);
}
for(ll i=1;i<=n;i++){
ans1[i]=(ans1[i]+ans2[i]-1)*a[i];
ans=max(ans1[i],ans);
}
cout<<ans<<endl;
}
return 0;
}
|
题意
- N个人正在排队进入一个音乐会,队列中任意两个人A和B,如果他们是相邻或他们之间没有人比A或B高,那么他们是可以互相看得见的。写一个程序计算出有多少对人可以互相看见;
- 洛谷蓝题,比前面两题多了点坑。
题解
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| #include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,a[500005];
ll ans[500005];
stack<ll> s;
ll anss;
int main(){
cin>>n;
for(ll i=1;i<=n;i++){
cin>>a[i];
ans[i]=1;
}
for(ll i=1;i<=n;i++){
while(!s.empty()&&a[i]>=a[s.top()]){
anss+=ans[s.top()];
if(a[s.top()]==a[i]) ans[i]+=ans[s.top()];
s.pop();
}
if(!s.empty()) anss++;
s.push(i);
}
cout<<anss<<endl;
return 0;
}
|
单调队列
概念
- 顾名思义,就是满足单调性的队列结构,可以是单调递增or递减or自己定义。
练习题
题意
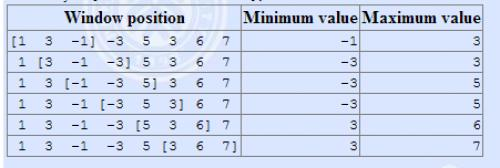
- 有一个长为$n$的序列$a$,以及一个大小为$k$的窗口,现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
Sample Input
Sample Output
| -1 -3 -3 -3 3 3
3 3 5 5 6 7
|
题解
AC代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| #include<bits/stdc++.h>
using namespace std;
deque<int> q1;
deque<int> q2;
int a[1000005];
int main(){
int n,k;
cin>>n>>k;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
for(int i=1;i<=n;i++){
while(!q2.empty()&&a[i]<a[q2.back()]){
q2.pop_back();
}
q2.push_back(i);
if(i-k+1>q2.front()) q2.pop_front();
if(i>=k) cout<<a[q2.front()]<<" ";
}
cout<<endl;
for(int i=1;i<=n;i++){
while(!q1.empty()&&a[i]>=a[q1.back()]){
q1.pop_back();
}
q1.push_back(i);
if(i-k+1>q1.front()) q1.pop_front();
if(i>=k) cout<<a[q1.front()]<<" ";
}
return 0;
}
|
- 总体来说单调栈的思维灵活性和难度更大一些,当然单调队列也十分有用,都需要细品。