MergeSort理解

【复习】 归并排序原理（MergeSort）

• 经典排序算法之一：归并排序（MergeSort），时间复杂度为$nlogn$，这里复习一遍。
• 以我目前所学知识而言，归并排序最常用的还是用来解决逆序对的问题，以及其合并数组的思想可以用来解决许多难题，如多人背包中合并dp数组的方法就利用了归并排序的思想。

---

归并排序

原理解释

核心步骤：

1. 我们先开一个数组合并空间，用来存储每次排好序的序列；

2. 对于一个无序序列，我们不断将其二分为若干组，直到每一组只剩下一个元素为止（此刻也即是每一组都是有序的了）；

3. 设定两个指针，最初位置分别为两个已经排好序的序列的起始位置；

4. （递归地）从最后两个组分逐步向前，比较两串已经排好序的序列的各个元素（一顿排序工作,这个时候可以发现逆序对！），将较小的元素先放入合并空间，并同时移动指针，完成一轮排序；

5. 将上步骤中两组剩余的（未放入合并空间的or指针还未指向尾部的）元素继续放入合并空间；

6. 将排序好的合并序列赋值给左边的序列，以便下一轮递归使用；

7. 重复3、4、5、6操作，直至整个序列有序。

帮助理解的图

---

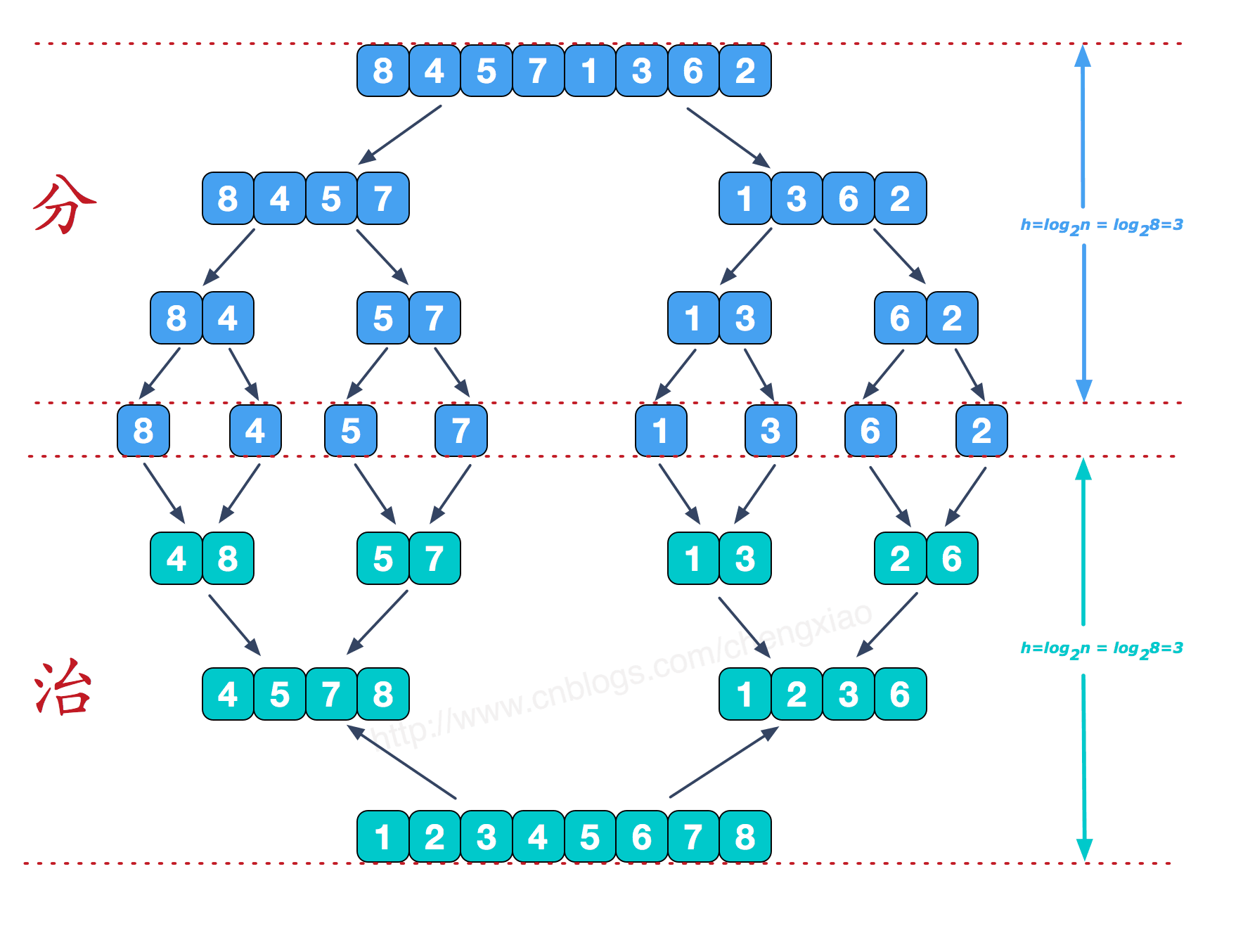
核心代码

int s[maxn],p[maxn];
void msort(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1;
	msort(l,mid);msort(mid+1,r); //不断二分
    int i=l,j=mid+1,t=l; 
	while(i<=mid&&j<=r){
		if(s[i]>s[j]) p[t++]=s[i++];
        p[t++]=s[j++];
    }
    while(i<=mid) p[t++]=s[i++];
    while(j<=r) p[t++]=s[j++];
    for(int k=l;k<=r;k++) s[k]=p[k];
    return;
}

模板代码（逆序对版本）

#include<bits/stdc++.h>
using namespace std;

const int maxn = 10000005;
int s[maxn],p[maxn];
long long ans; //逆序对个数

void msort(int l, int r){
	int mid = (l+r)>>1;
	if(l==r) return;
	msort(l,mid);msort(mid+1,r);
	int i = l, j=mid+1,t=l;
	while(i<=mid&&j<=r){
		if(s[i]>s[j]){
			ans += mid-i+1; //出现逆序对，开始计数
			p[t++] = s[j++];
		}
		else p[t++] = s[i++];
	}
	while(i<=mid) p[t++]=s[i++];
	while(j<=r) p[t++]=s[j++];
	for(int k=l;k<=r;k++) s[k]=p[k];
	return;
}

int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>s[i];
	msort(1,n);
	cout<<ans<<endl;
	return 0;
}

---