简单理解勒让德变换

勒让德变换的热力学简单理解

“哥哥，我想换个变量!”

勒让德变换(Legendre transformation)

• 最近在搞热统，在回顾热力学基本方程的时候发现了这么个玩意儿，但由于本人没系统学习过分析力学，这里仅谈一下对该变换比较浅层的理解（仅针对热力学的理解）。

---

当然定义还是要说一下的啦：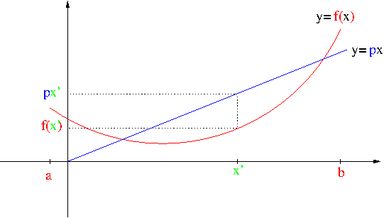

从纯数学角度来说，对于一个上凸函数 $y=px-f(x)$（其中$f(x)$为下凸函数，且是可微的）对其求导，导数为零，满足

$$p=\frac{df}{dx}$$

这样从 $x$ 到 $p$ 建立起一个映射，即$x$到曲线斜率的映射。
我们令 $x=g(p)$，即 $p$ 到 $x$ 的逆映射存在（就是反函数啦），因为 $f(x)$ 是一个下凸函数，其斜率与曲线上的点是一一对应的。
这样，我们就定义了一个新的函数与 $f$ 相对应：

$$f^*(p)=g(p)\cdot p-f(g(p))$$

该函数是以 $p$ 为自变量的函数。从 $f$ 到 $f^* $ 的变换就称为勒让德变换，即把原来在的 $f$ 对应于一个它的对偶空间的 $f^* $ 。

能原谅我其实没太看懂吗

理解

• 最简单的理解就是：这个自变量不好看，我换一个自变量。
• 往应用方面去理解的话，可以这么说：在表示一个系统的时候，往往有多种表示方法，每种表示方法之间可以通过勒让德变换来构建联系。（或者说：我想换个变量，怎么办？勒让德变换！）

热力学应用

举个简单的栗子：

热力学基本方程：$dU=TdS-PdV$，噢这里自变量是$S$和$V$，那我想要自变量变成$S$和$P$咋办呢？

我们知道，热力学能（$U$）是一种热力学势，由上述方程可知它是自然变量$S$和$V$的函数：$U(S,V)$，而想要改写成$S$和$P$的函数关系，似乎就需要引入一个新的热力学势，这个热力学势就是焓(H)，整个过程的呈现如下：

$$dU=TdS-PdV$$

等号两边作如下变换：

$$dU+d(PV)=TdS-PdV+PdV+VdP$$

化简：

$$d(U+PV)=TdS+VdP$$

yep！这个等号左边微分符号内就是我们所说的 焓($H=U+PV$) 啦,因此有:

$$dH=TdS+VdP$$

---

以上过程就是热力学中的勒让德变换的简单应用啦！

• 当然，还有其他的热力学势，如：亥姆霍兹自由能($A(T,V)$)和吉布斯自由能($G(T,P)$)，均可以由基本方程和勒让德变换获得，笔者将继续摸索下去。